Статья опубликована в №69 (май) 2019
Разделы: Информационные технологии
Размещена 01.05.2019. Последняя правка: 30.04.2019.
Просмотров - 1126

ОРГАНИЗАЦИЯ РЕШАЮЩИХ ПОЛЕЙ ПРЕОБРАЗОВАНИЯ ДАННЫХ

Князькова Анна Владимировна

Аспирант

Вятский государственный университет

Кафедра электронных вычислительных машин

Страбыкин Д.А., доктор технических наук, профессор, Вятский государственный университет

УДК 681.32

Введение. В настоящее время в ведущих научных центрах и исследовательских лабораториях мира проводятся интенсивные исследования по созданию средств компьютерной техники новых поколений. Одним из активно развиваемых направлений является создание высокопроизводительных ЭВМ и систем, предназначенных для решения комбинаторно-логических задач большой размерности. [1]

Современные типы ЭВМ и систем не позволяют сегодня решать комбинаторно-логические задачи большой размерности за приемлемое время. Это, прежде всего, обусловлено несоответствием алгоритмических решений такого типа задач принципам организации вычислений и особенностями архитектуры современных универсальных ЭВМ и систем.
Актуальность. Анализ современного программного обеспечения для решения задач в различных прикладных областях показывает, что доля численных операций составляет лишь 20% от общего объема операций, а 80% составляют логические и поисковые операции и операции преобразования данных. В связи с этим в целом сегодня стоит задача создания ЭВМ и систем с нетрадиционной архитектурой (архитектурой, направленной на эффективную реализацию не численных операций с данными), в частности, для комбинаторно-логической обработки массивов данных большой размерности. [2,3]

Целью исследования является повышение быстродействия вычислительной системы. Это может быть осуществлено двумя подходами. Первый подход заключается в организации параллельных вычислительных процессов, за счет введения избыточности функциональных устройств. В этом случае достигается ускорение процессов решения вычислительной задачи путем выполнения декомпозиции данных, вычислительных функций и коммуникационных процессов обмена данными на независимые части, а также организации обработки таких частей на разных процессорах или процессорных секциях. Такой классический подход позволяет ускорить вычисления и, соответственно, сократить время решения прикладной задачи.

Вторым направлением совершенствования вычислительных систем для решения комбинаторно-логических задач является включение в их состав функционально-ориентированного аппаратного обеспечения, которое предназначено для выполнения процедур, трудно реализуемых средствами универсальных ЭВМ. [4] Опыт показывает, что при таком подходе достигается увеличение как номинальной, так и пользовательской производительности вычислительных систем за счет распараллеливания и аппаратно-программной реализации вычислительного процесса на несколько порядков.

Таким образом, задачами исследования являются:

- выбор операций преобразования структур данных, наиболее часто встречающихся среди операций обработки;

- составление системы логических функций для реализации выбранных операций;

- разработка логической схемы, реализующий выбранный набор операций преобразования структур данных;

-  выбор структуры вычислительного пространства.

Научная новизна. Научная новизна исследования заключается в выборе основных операций преобразования структур данных, трудно реализуемых классическими средствами ЭВМ и систем, и разработке функционально-ориентированного аппаратного обеспечения, которое предназначено для выполнения выбранного набора процедур.

Основная часть.

Решающее поле процессорных элементов является одним из главных элементов вычислительных систем с параллельной или частично-параллельной организацией обработки данных. В таких системах должна быть обеспечена не только возможность доступа к данным одного элемента памяти, но и возможность записи или считывания по строкам или столбцам массивов данных, то есть должна быть обеспечена организация работы с векторами и матрицами.[5]

Наряду с этим, в системах с параллельной обработкой особое значение приобретают операции преобразования структур данных перед выполнением массовых операций. Чтобы обеспечить высокую эффективность системы в целом, необходимо использовать специальные аппаратные средства, выполняющие достаточно широкий набор операций преобразования структур данных (сжатие произвольного вектора, расширение, сплетение векторов, перегруппировка и взвешивание с маскированием) с большой скоростью. Рассмотрим подробнее перечисленные операции.

Сжатие.

Сжатием произвольного вектора f называется операция x ← z/f, где z – управляющий двоичный вектор, размерность которого совпадает с размерностью входного вектора f. Результат операции – произвольный вектор x, который содержит только те компоненты вектора f_i, которые соответствуют единичным элементам вектора z_i. Размерность вектора x равна числу единиц вектора z. Пример этой операции показан на рисунке 1.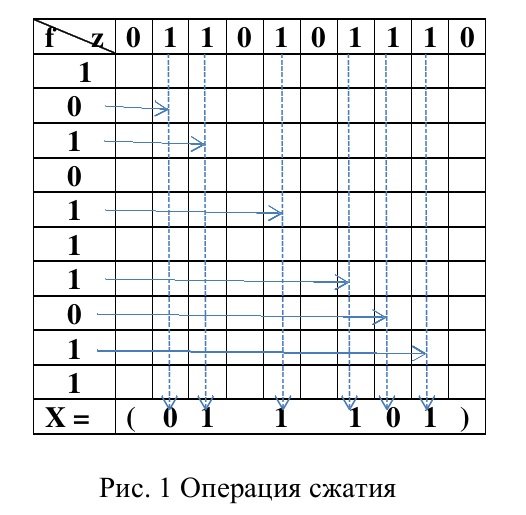 

Расширение. Расширением произвольного вектора f называется операция x ← zf, где z – управляющий двоичный вектор, размерность которого не меньше размерности вектора f. Результат операции – произвольный вектор x, в котором компоненты исходного вектора f_i занимают позиции, которые соответствуют единичным элементам вектора z_i. Компоненты xi, соответствующие нулям вектора z, содержат нули. Пример операции расширения показан на рис.2 

Сплетение. Сплетением называетсяоперация x←f, z, g, которая по двум произвольным векторам fи gи управляющему вектору z строит вектор x так, что компоненты x_i принимают значения очередных компонент f_i либо g_i в зависимости от значения z_i (0 либо 1). Размерность вектора x совпадает с размерностью вектора z и равна сумме размерностей f и g. Пример этой операции показан на рис. 3. 

Перегруппировка. Перегруппировкой произвольного вектораfназывается операция x←f ∆ z, где z – управляющий двоичный вектор, размерность которого равна размерности вектора f. Результат операции – произвольный вектор x, который в качестве n первых компонент x_j содержит те компоненты f_i исходного вектора f, которые соответствуют z_i=0. Размерность вектора x совпадает с размерностью вектора z и равна n+m, где
n и m –количество единиц и нулей вектора z соответственно.

Взвешивание с маскированием. Взвешиванием с маскированием называется операция x← z f, где z – управляющий двоичный вектор, размерность которого равна размерности вектора f. Результат операции – произвольный вектор x, который содержит только единичные компоненты исходного вектора f, которые соответствуют поразрядно z_i=1. Размерность вектора x равна количеству единиц в результирующем векторе при операции логического умножения векторов f и z. Пример этой операции проиллюстрирован на рис. 4.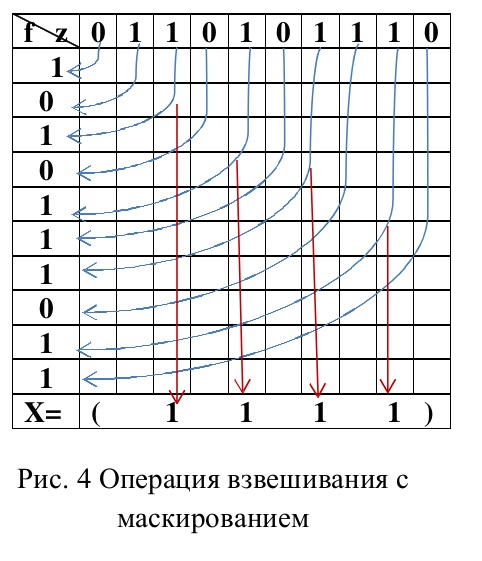 

В результате анализа было выявлено, что для реализации перечисленных выше операций, общая система логических функций ячейки решающего поля имеет вид:

t′ = t ‾zy

z′ = fz‾t˅ yz‾t

x′ = x ˅ ztf

f′ = f

y′ =y

Реализация операций преобразования данных таким образом может выполняться логической ячейкой решающего поля, представленной на рис. 5.



В состав схемы входят четыре вентиля «И» и четыре вентиля «ИЛИ».

Для выполнения таких операций, как сжатие, расширение и взвешивание с маскированием, достаточно решающего поля в виде треугольной матрицы. Если же в операции участвуют два исходных вектора, (операция сплетения) или необходимо использовать два режима в организации управления (операция перегруппировки), то решающее поле должно быть организовано в виде двух треугольных матриц как показано на рис.6. 

Результатами работы являются:

- сформирован набор операций преобразования структур данных, наиболее часто встречающихся среди операций обработки данных;

- составлена система логических функций для реализации выбранных операций;

- разработана логическая схема ячейки, реализующая выбранный набор операций преобразования структур данных;

-  обоснован подход выбора структуры вычислительного пространства в виде однородной структуры;

- разработана структура  решающего поля для выделенного типа операций.

Заключение. Технологии изготовления кристаллов на сегодняшний день достигли такого уровня, что нет проблем в изготовлении подобных решающих полей больших размерностей. Таким образом, организация вычислительного процесса обработки информации в таком решающем поле позволит выполнять операции преобразования данных значительно быстрее, чем при решении подобных задач на вычислительных структурах традиционной архитектуры с использованием программного обеспечения.

1. Старченко А.В., Есаулов А.О. Параллельные вычисления на многопроцессорных вычислительных системах. Томск:ТГУ, 2002
2. Knyazkov V.S., Volchenskaya T.V. Algebraic Fundamentals of Massive Computation // Proceeding of the Fourth Intern. Conf. Of Science and Technology “New Information Technologies and Systems”, Penza, Russia, December, 2000.- pp. 88-89.
3. Knyazkov V.S., Volchenskaya T.V. Method of Organization and Complexity of Sequentially –bit Mass Processing // Proceeding of the Fourth Intern. Conf. Of Science and Technology “New Information Technologies and Systems”, Penza, Russia, December, 2000.- pp. 87-88.
4. Волченская Т. В., Князьков В. С. Спецпроцессоры для решения задач на графах. Научный журнал Advanced science № 3, ПРИП ФГБОУ ВПО «ВятГУ» , Киров, 2013, С. 73-82.
5. Волченская Т.В., Князьков В.С. и др. Многофункциональная ячейка однородной структуры. Патент .№ 1663609 , G06F7/00, октябрь 1993 г.

Комментарии пользователей:

14.05.2019, 22:02 Усманова Ирина Викторовна Отзыв: Статья посвящена распределенным вычислениям на основе решающих полей, что является весьма актуальным на сегодняшний день. Видна глубокая проработка вплоть до решения в виде функционально-логической схемы базовой ячейки реализации основных операций преобразования данных. Однако, из статьи не совсем понятно управление настройки решающего поля, представленного на рис.6. В целом, работу можно оценить положительно и рекомендовать к публикации.

16.05.2019, 13:39 Васин Леонид Анатольевич Отзыв: В статье рассматривается проблемы решения комбинаторно-логических задач ориентированных на большую размерность. Предложены пути решения на основе специального функционально-ориентировнного аппаратного обеспечения в составе универсальной ЭВМ. Показан вариант построения логической ячейки и решающего поля. В работе, автором предложен подход к решению такой задачи, основанный на использовании решающего поля выполненного в виде двух треугольных матриц реализуемых на базе на логической ячейки. Это позволяет выполнять операции преобразования структур данных (сжатие произвольного вектора, расширение, сплетение векторов, перегруппировка и взвешивание с маскированием) с большой скоростью. Данная статья может быть рекомендована к публикации.

31.05.2019, 13:16 Коржавина Анастасия Сергеевна Отзыв: Статья посвящена актуальной проблеме -- разработке ЭВМ и систем с нетрадиционной архитектурой для комбинаторно-логической обработки массивов данных большой размерности -- и вызывает практический интерес. Материал работы хорошо структурирован, выводы сделаны. В целом, данная статья выполнена в соответствии с требованиями и может быть рекомендована к публикации.

31.05.2019, 22:39 Пляскин Степан Андреевич Отзыв: В статье приведен способ повышения быстродействия вычислительной системы за счёт включения в их состав аппаратного обеспечения, предназначенного для обработки массивов данных большой размерности. Проблемы повышения быстродействия и увеличения размерности обрабатываемых данных являются актуальными. Автором проделана комплексная работа: от выделения операций над массивами данных большой размерности до разработки структуры решающего поля, ячейка которого описана логической схемой с элементами И, ИЛИ, НЕ. Не являются очевидным назначение сигналов «t» и «y». Статья может быть рекомендована к публикации.

Оставить комментарий