Разделы: Математика, Спорт
Размещена 21.03.2022. Последняя правка: 22.07.2022.
Просмотров - 1814

Математическая игра «Империи»

Харт Алекс

Индивидуальный предприниматель

Индивидуальный предприниматель

УДК 51-8; 794.4; 794.02; 511

Введение

В логические игры люди играют уже достаточно давно. К ним относятся шахматы, шашки. Также многие карточные игры, несмотря на то, что в них велик фактор случайности в победе, тем не менее, также заставляют человека думать. С появлением же персональных компьютеров, планшетов и мобильных телефонов появилось огромное множество различных логических игр.

Актуальность

В работах [1] и [2] определено математическое понятие заполненность разрядов чисел. Данное понятие позволяет разделять числа, например, на сильные и слабые, давая количественную характеристику соответственно силы или слабости того или иного числа (в определенной системе счисления). В связи с этим актуально показать применение данной характеристики чисел в логических играх, основанных на числах.

Цели

Используя математическое понятие фактическая заполненность разрядов чисел, предложить игру, в которую можно было бы играть как с помощью игральных карт на столе, так и на персональном компьютере, планшете или мобильном телефоне.

Научная новизна

С появлением вычислительной техники появилось множество логических игр, основанных на числах. Игры же, основанной на таких свойствах чисел, как сила или слабость, которые описываются математическим понятием заполненность разрядов чисел, еще предложено не было.

Вниманию читателей предлагается игра «Империи». В данной игре используется математическое понятие фактическая заполненность разрядов чисел, которое определено в работах [1] и [2]. Каждая империя имеет свои масштаб и силу, которые могут меняться со временем. Масштаб империи определяется тем или иным числом. А сила империи определяется фактической заполненностью разрядов этого числа (в десятичной системе счисления).

Таким образом, все империи характеризуются определенным числом, равным их масштабу. Фактическая заполненность разрядов этого числа определяет силу той или иной империи. Как показано в работе [2], фактическая заполненность разрядов представляет собой перевернутую запись числа в соответствующей системе счисления. Поэтому определить, какое из чисел сильнее, довольно легко. Для этого нужно поразрядно сравнивать числа, начиная с конца. Например, какое число сильнее, 129 или 49? Смотрим с конца. Первый разряд у обоих чисел равен 9. Они равны. Идем дальше. Второй разряд у первого числа равен 2, а у второго – 4. Значит второе число сильнее первого, несмотря на то, что первое число больше второго.

В игру «Империи» можно играть как с помощью игральных карт на столе, так и на персональном компьютере, планшете или мобильном телефоне. В первом случае игра «Империи» может также называться игра «Короли». «Женский» вариант игры «Короли» может называться игра «Дамы» (см. ниже).

Правила игры «Короли».

1. В игре участвуют 54 карты. Количество участников от 2 до 4. (Если используется две колоды карт (108 карт), то максимальное количество участников равно 8.)

2. В начале игры карты раскладываются на столе в виде прямоугольника 9х6 (если используется две колоды карт, то 12х9) лицевой стороной вверх («в открытую»). Также возможна разновидность игры «в закрытую». В этом случае лицевой стороной вверх кладутся только короли, остальные карты кладутся лицевой стороной вниз (см. рис. 1).

 

 

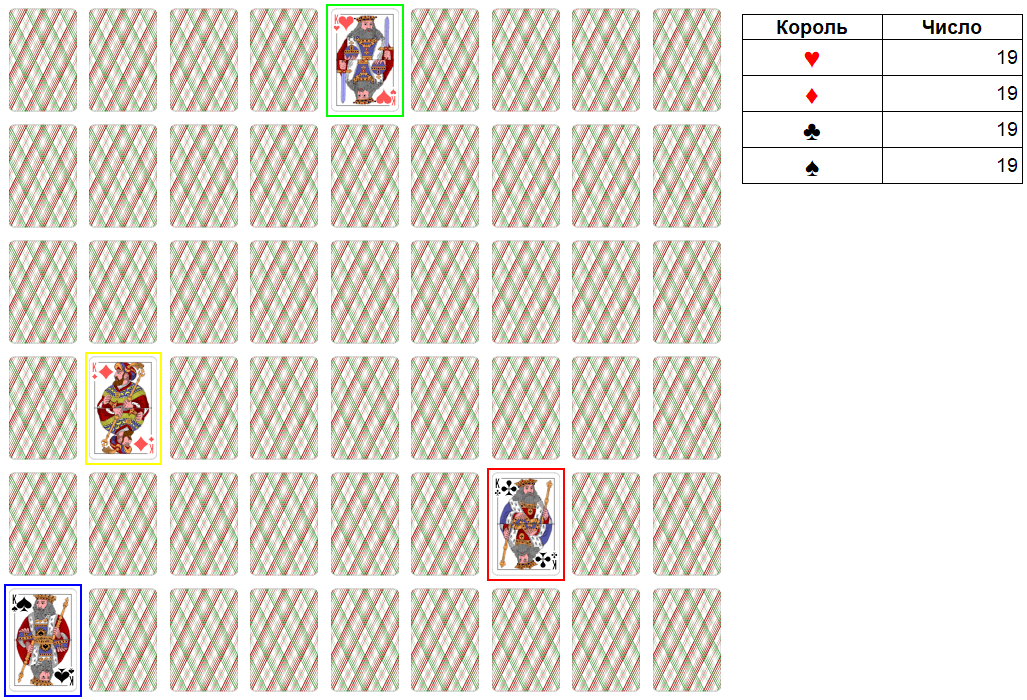
Рис. 1. Пример начальной расстановки карт игры «в закрытую».

 

3. В начале игры каждый игрок это тот или иной король. И цель игры каждого участника заключается в расширении империи своего короля путем присоединения к ней других карт.

4. Определяется порядок ходов королей. Он может быть произвольным. Например, порядок может определяться исходя из расположения королей, слева направо и сверху вниз (как чтение текста).

5. Каждая карта имеет определенное число, достоинство. Карты с 2 по 10 имеют такое же число, равное самому себе: 2 – 2, 3 – 3 и т.д. Валет имеет число 11, дама – 15, король – 19, туз – 1, джокер – 0. Если сложить числа всех карт, то мы получим общее число, равное 400 (игра «четырехсотка»), по 100 очков на каждую масть. Возможна разновидность игры, в которой джокер имеет число 50. В этом случае общее число будет равно 500 (игра «пятисотка»). Масть карт роли не играет.

6. Ход каждого короля заключается в присоединении к своей территории близлежащих карт. При этом итоговое число его империи (масштаб) будет равно сумме всех чисел карт, находящихся в ней (см. рис. 2).

 

 

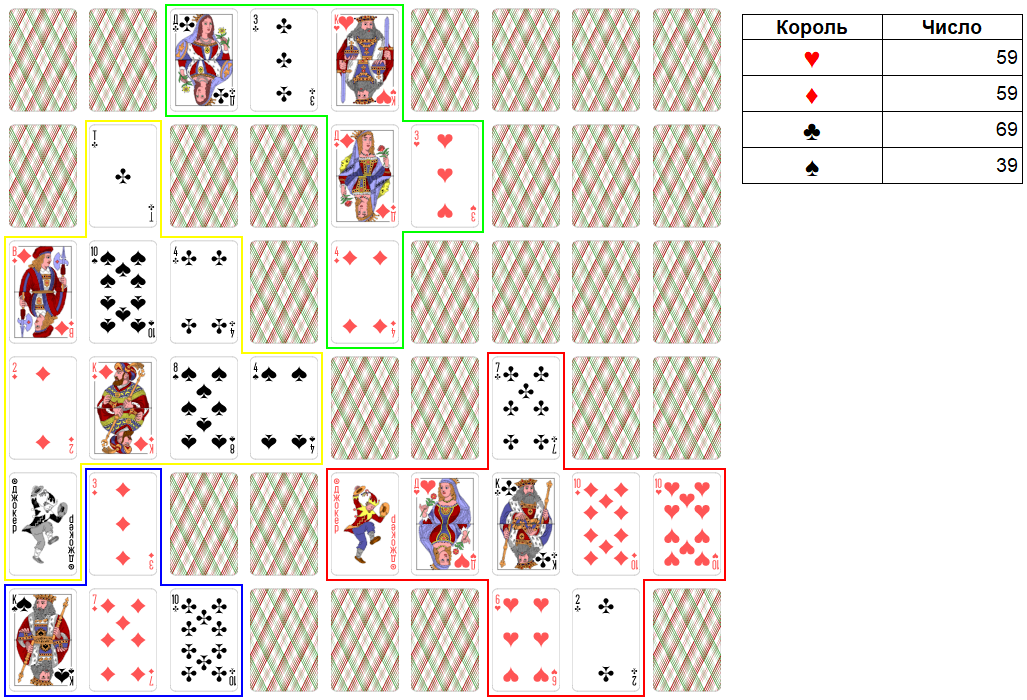
Рис. 2. Расширение территорий королей.

 

7. Итоговое число определяет масштаб империи того или иного короля. А фактическая заполненность разрядов этого числа (в десятичной системе счисления) определяет силу его империи. Например, имеем две империи с итоговыми числами 127 и 39. Масштаб первой империи больше, чем масштаб второй. А сила первой империи меньше, чем сила второй. Король с итоговым числом 127 не может напасть на короля с итоговым числом 39 и присоединить к своей империи часть его карт. Напасть может только более сильный король на более слабого. Данное правило распространяется и на присоединение к империи короля отдельных карт (не включенных ни в какую империю). Например, империя короля с итоговым числом 33 не может присоединить к себе такие отдельные карты: 4, 5, 6, 7, 8, 9, дама (15), король (19).

8. Масштаб территорий королей имеет такую градацию: итоговое число от 0 до 9 – княжество, от 10 до 99 – королевство, от 100 – империя. Т.е. однозначные числа – это княжество, двузначные – королевство, трехзначные – империя.

9. Задача каждого хода короля присоединить к своей империи максимальное количество близлежащих карт. Естественно только тех, которые входят в состав более слабых империй. Но имеет смысл присоединять не все возможные карты, а лишь те, которые с одной стороны дадут максимальный масштаб империи, а с другой максимальную ее силу. Не стоит присоединять абсолютно все возможные карты, если это приведет к тотальному ослаблению империи. Но нужно смотреть по обстоятельствам.

10. Если какой-либо король захватывает другого короля, а у последнего имеются подчиненные карты (т.е. его территория не состоит из одной карты – его самого), то его империя продолжает существовать, а ее центром становится какая-либо другая карта. Возможна разновидность игры, когда при захвате того или иного короля (столицы империи), его империя перестает существовать, и все входящие в нее карты становятся независимыми.

11. Игра заканчивается, когда расширение империй королей больше не происходит. При этом в конце игры может остаться как одна империя, захватившая все карты и имеющая итоговое число 400 (или 500), так и четыре империи с разными итоговыми числами. Каждый игрок получает в конце игры количество очков, равное итоговому числу его империи.

12. В игре могут заключаться выгодные договоренности между разными участниками. Эти договоренности могут быть самые разные. Единственное условие таких договоренностей это максимальная выгода всех их участников. Например, королю бубен предлагает король виней заключить договор, чтобы они объединились против двух других королей и в случае победы поделили 400 очков пополам. А король червей предлагает аналогичные условия, только в случае победы король бубен получит 250 очков, а король червей 150. Естественно в такой ситуации король бубен должен заключить более выгодный союз с королем червей. Если тот или иной король уверен, что он может захватить все карты, т.е. все 400 (или 500) очков, в одиночку, то ему не нужно ни с кем заключать союз. Возможна разновидность игры, в которой никакие договоренности не заключаются, и каждый игрок может рассчитывать только лишь на себя.

Игра «Дамы» имеет аналогичные правила, что и игра «Короли». Только вначале игры каждый игрок это та или иная дама. При этом достоинство короля равно 15, а дамы – 19.

Приведем пример игры «Короли» по написанным выше правилам. Игра будет «в открытую» до 400 очков.

Пример игры.

Начальная расстановка карт:

 

 

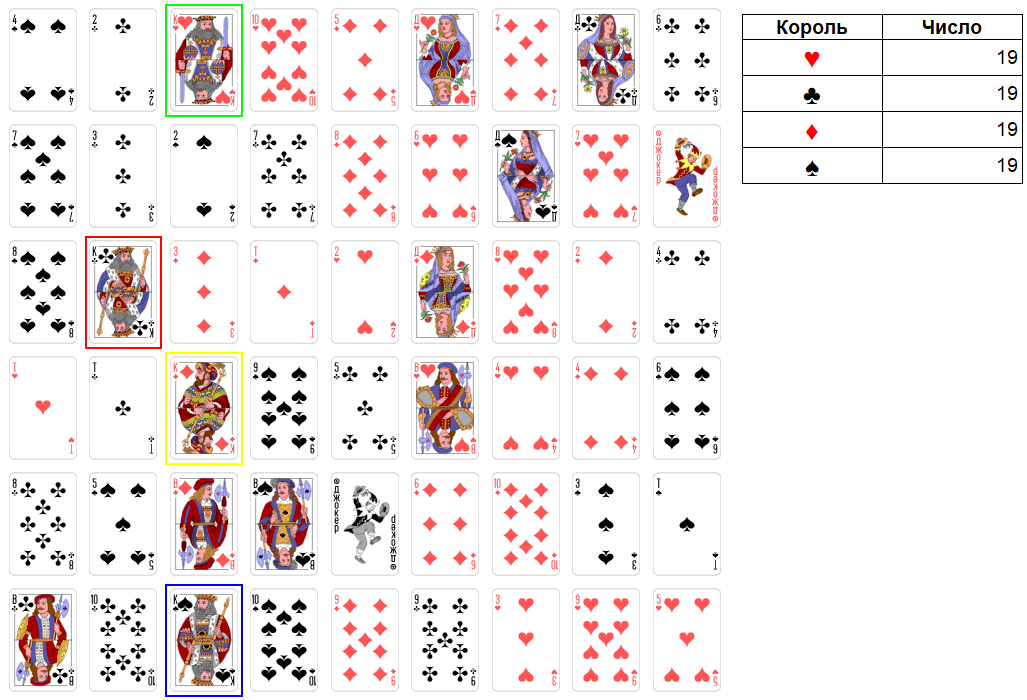
Рис. 3. Начальная расстановка карт.

 

Порядок ходов: король червей, король крестей, король бубен, король виней.

Раунд 1.

Ход короля червей. Максимально можно взять три карты достоинством: 2, 10, 2. Итоговое число станет равно 33. Это слабое число. Поэтому имеет смысл не брать 2 крестей и 2 виней. Итоговое число будет равно 29.

 

 

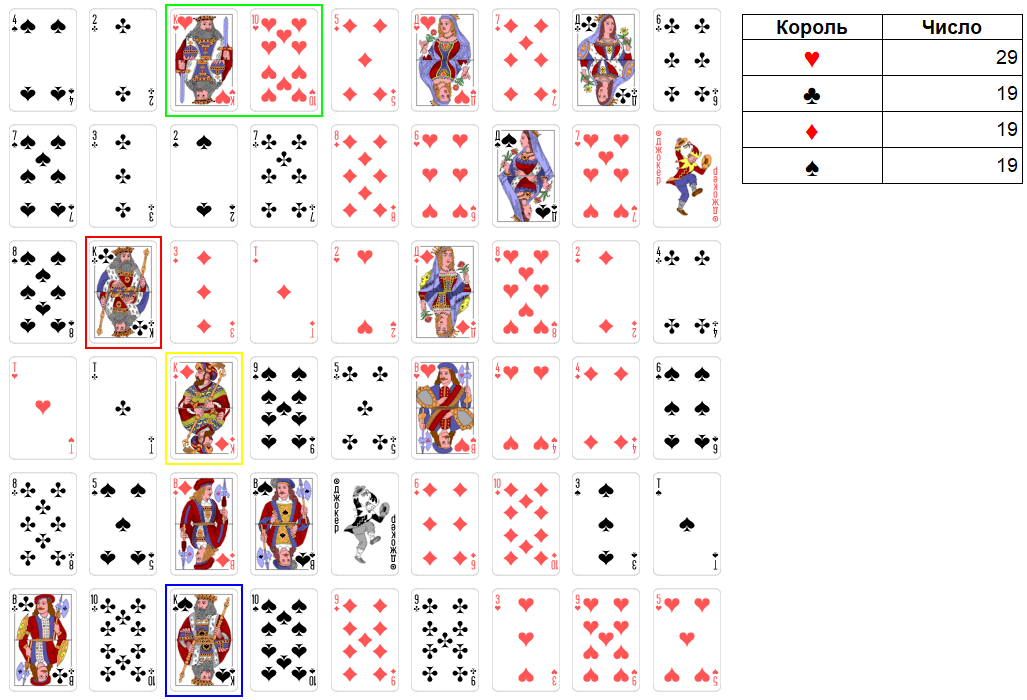
Рис. 4. Раунд 1. Ход короля червей.

 

Ход короля крестей. Максимально можно взять четыре карты достоинством: 3, 8, 3, 1. Итоговое число станет равно 34. Это слабое число. Поэтому имеет смысл не брать 3 крестей и 3 бубен. Итоговое число будет равно 28.

 

 

Рис. 5. Раунд 1. Ход короля крестей.

 

Ход короля бубен. Максимально можно взять четыре карты достоинством: 1, 3, 9, 11. Итоговое число станет равно 43. Это слабое число. Поэтому имеет смысл не брать туза крестей и 3 бубен. Итоговое число будет равно 39.

 

 

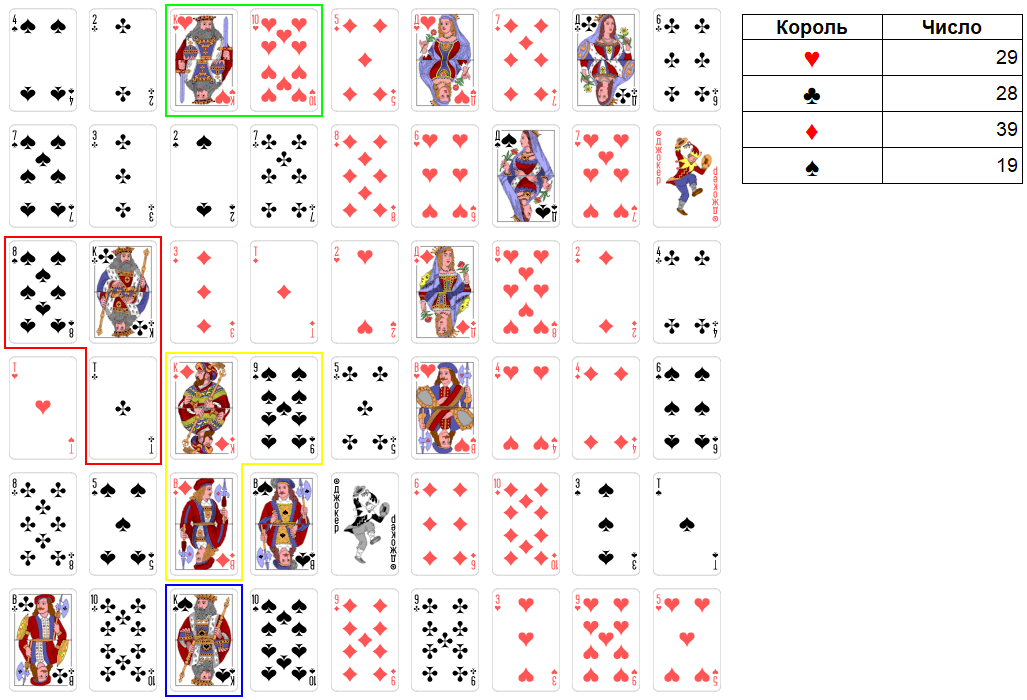
Рис. 6. Раунд 1. Ход короля бубен.

 

Ход короля виней. Максимально можно взять две карты достоинством: 10, 10. Итоговое число станет равно 39. Это сильное число. Отобрать вальта бубен у короля бубен король виней не может, так как первый король сильнее второго. Но, взяв 10 крестей и 10 виней, король виней догоняет короля бубен в силе.

 

 

Рис. 7. Раунд 1. Ход короля виней.

 

Раунд 2.

Ход короля червей. Максимально можно взять четыре карты достоинством: 2, 5, 2, 7. Итоговое число станет равно 45. Это не сильное число. Поэтому имеет смысл не брать 7 крестей. Итоговое число будет равно 38. 5 бубен имеет смысл взять, так как за ней идет дама червей, сразу 15 очков.

 

 

Рис. 8. Раунд 2. Ход короля червей.

 

Ход короля крестей. Максимально можно взять пять карт. Итоговое число станет равно 47. Это не слабое число. Но территория короля крестей примыкает к территории короля бубен, и будет примыкать к территории короля виней, а последние два короля имеют сильное число 39. Поэтому имеет смысл не брать 7 виней и туза червей. Итоговое число будет равно 39. Вместо 7 и туза можно также не брать 3 и 5. Но 7 и туз расположены с краю, а обе 3 и 5 ближе к центру. Поэтому попробуем не брать все-таки 7 и туза.

 

 

Рис. 9. Раунд 2. Ход короля крестей.

 

Ход короля бубен. Максимально можно взять три карты достоинством: 1, 5, 11. Итоговое число станет равно 56. Это не сильное число. Учитывая, что к территории короля бубен примыкают территории двух сильных королей. Король бубен может что-то не брать. Но при любом возможном расширении своей территории он неизбежно ослабнет. Можно конечно не брать ничего, но такая тактика отодвинет нападение на короля бубен лишь на один ход. Король бубен будет договариваться или с королем крестей, или с королем виней. Но король виней не будет договариваться ни о чем с королем бубен, так как на своем следующем ходе он возьмет вальта крестей и 9 бубен, усилив себя до итогового числа 59. А король крестей будет договариваться с королем бубен, так как король виней угрожает и ему. Оба короля, король крестей и король бубен, расположены в середине между королем червей и королем виней. Поэтому договоренность между ними необходима. Они договорятся так. Король бубен захватывает сейчас максимальное количество карт, тем самым, ослабляя себя и позволяя королю крестей брать его карты на следующем ходе, усиливая себя. Но выигрыш будет пополам между ними. В противном случае король бубен не станет себя ослаблять, и оба этих короля могут проиграть с высокой вероятностью.

 

 

Рис. 10. Раунд 2. Ход короля бубен.

 

Ход короля виней. Максимально можно взять четыре карты достоинством: 11, 11, 11, 9. Итоговое число станет равно 81. Это очень слабое число. Имеет смысл взять только одного вальта и 9. Итоговое число будет равно 59. Причем имеет смысл брать именно вальта бубен, так как в этом случае король виней максимально отрежет территорию для расширения королю крестей.

 

 

Рис. 11. Раунд 2. Ход короля виней.

 

Раунд 3.

Ход короля червей. Максимально можно взять четыре карты достоинством: 4, 15, 7, 8. Итоговое число станет равно 72. Это очень слабое число. Поэтому имеет смысл не брать даму червей и 8 бубен. Итоговое число будет равно 49.

 

 

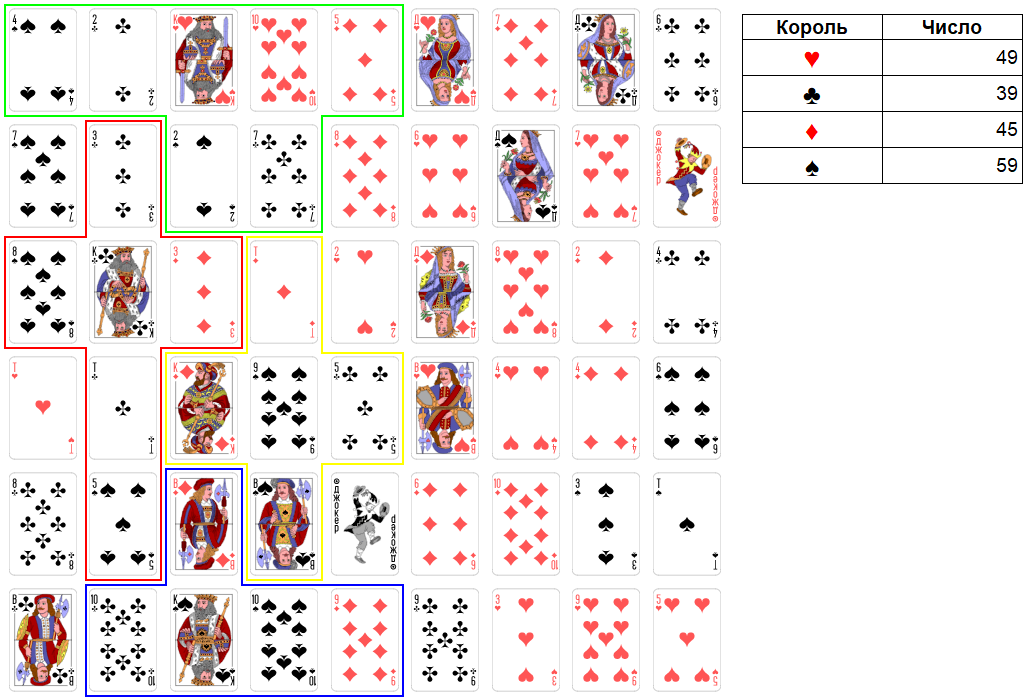
Рис. 12. Раунд 3. Ход короля червей.

 

Ход короля крестей. Максимально можно взять пять карт. Итоговое число станет равно 75. Это не сильное число. Поэтому имеет смысл брать только туза и короля. Итоговое число будет равно 59. Причем имеет смысл взять именно туза бубен, а не туза червей. Так как первый расположен в середине поля, а второй с краю. Король крестей догоняет в силе своего основного конкурента – короля виней. Поскольку король бубен захвачен, его территория управляется из 5 крестей. Но напомним, что короли крестей и бубен, по сути, объединились и делят победу на двоих.

 

 

Рис. 13. Раунд 3. Ход короля крестей.

 

Ход короля бубен. Максимально можно взять три карты достоинством: 2, 11, 0. Итоговое число станет равно 38. Это не слабое число. К тому же победа короля бубен зависит от победы короля крестей.

 

 

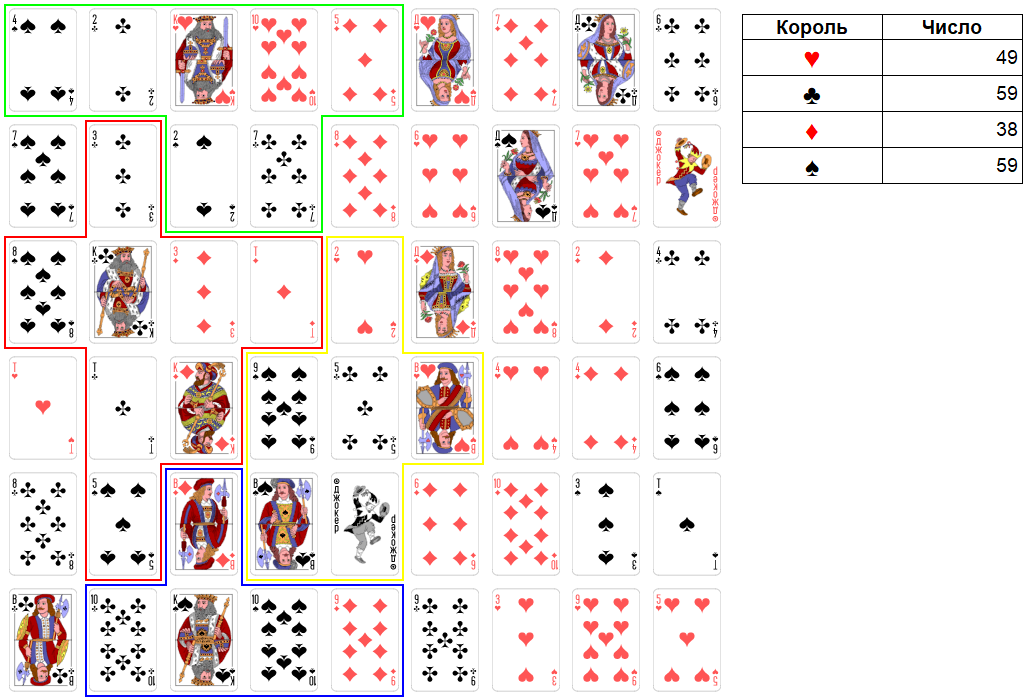
Рис. 14. Раунд 3. Ход короля бубен.

 

Ход короля виней. Максимально можно взять четыре карты достоинством: 11, 0, 11, 9. Итоговое число станет равно 90. Это очень слабое число. Имеет смысл не брать одного вальта. Итоговое число будет равно 79. Причем имеет смысл не брать именно вальта крестей, так как он находится в самом углу, а валет виней ближе к середине поля.

 

 

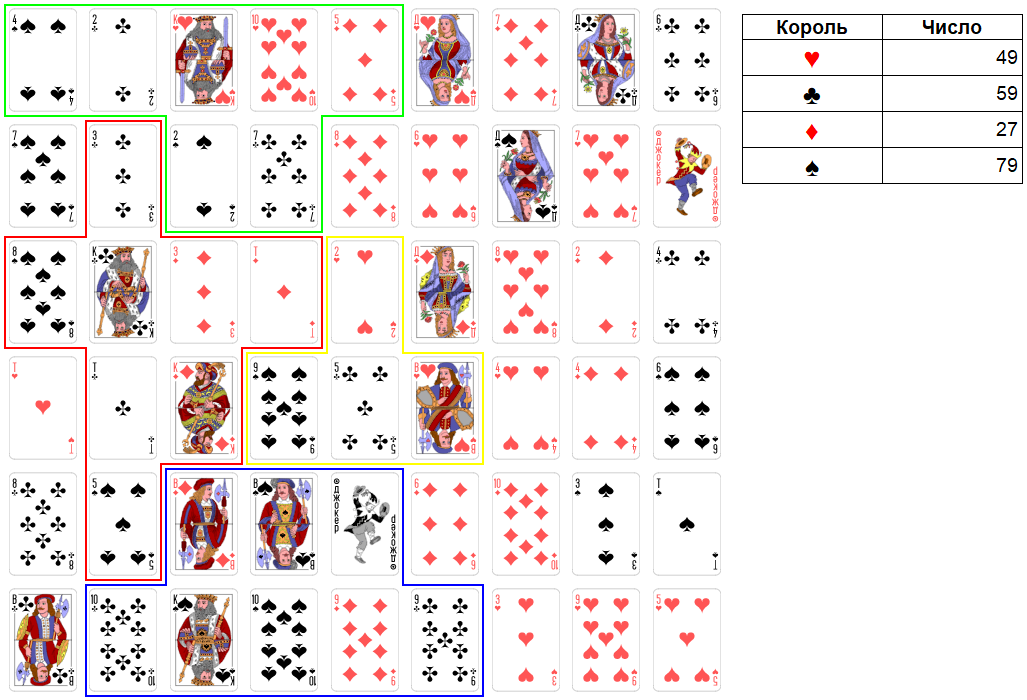
Рис. 15. Раунд 3. Ход короля виней.

 

Раунд 4.

Ход короля червей. Максимально можно взять три карты достоинством: 15, 7, 8. Итоговое число станет равно 79. Это сильное число. И граничащий к королю червей король крестей не сможет напасть на первого.

 

 

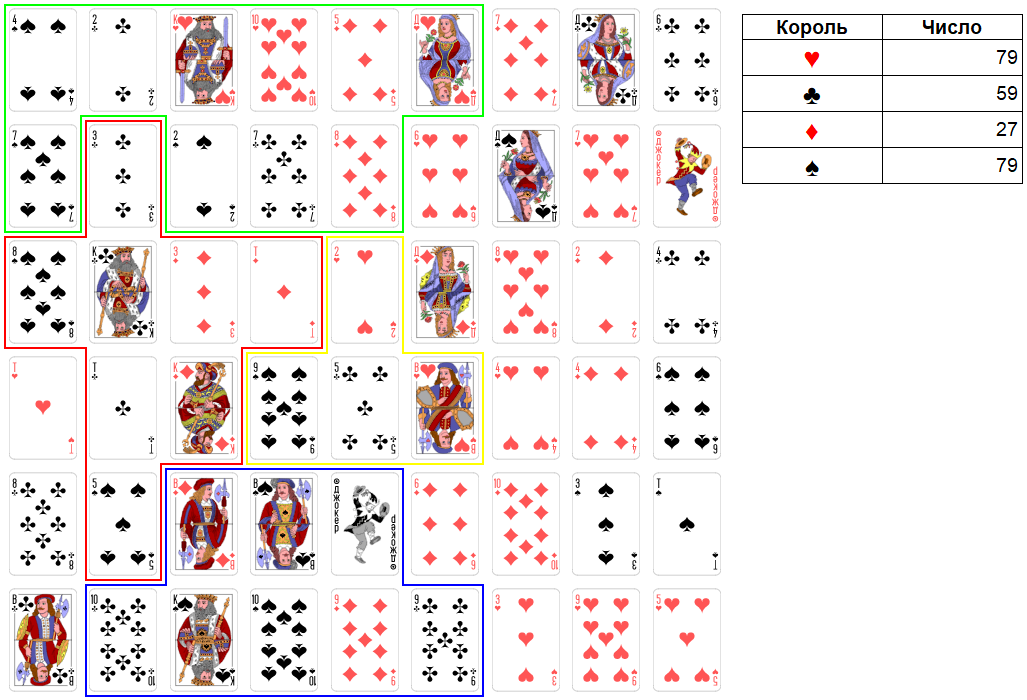
Рис. 16. Раунд 4. Ход короля червей.

 

Ход короля крестей. Максимально можно взять четыре карты достоинством: 1, 2, 9, 8. Итоговое число станет равно 79. Это сильное число. И у трех сильных королей итоговое число будет равно 79.

 

 

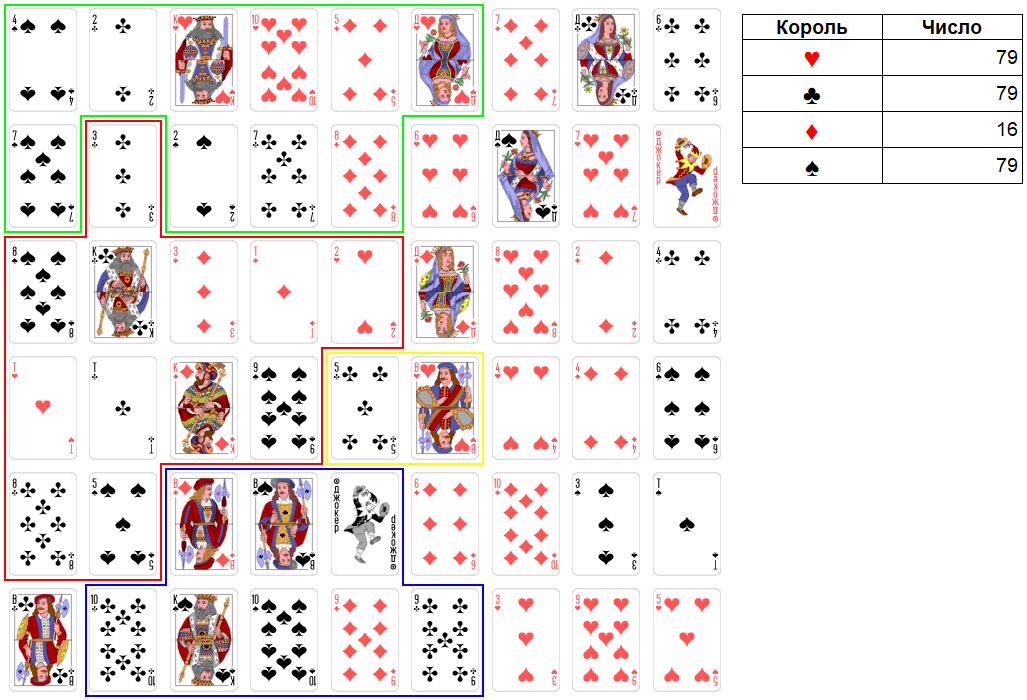
Рис. 17. Раунд 4. Ход короля крестей.

 

Ход короля бубен. Максимально можно взять три карты достоинством: 15, 4, 6. Итоговое число станет равно 41. Это очень слабое число. Но это не важно. У короля бубен договор с королем крестей.

 

 

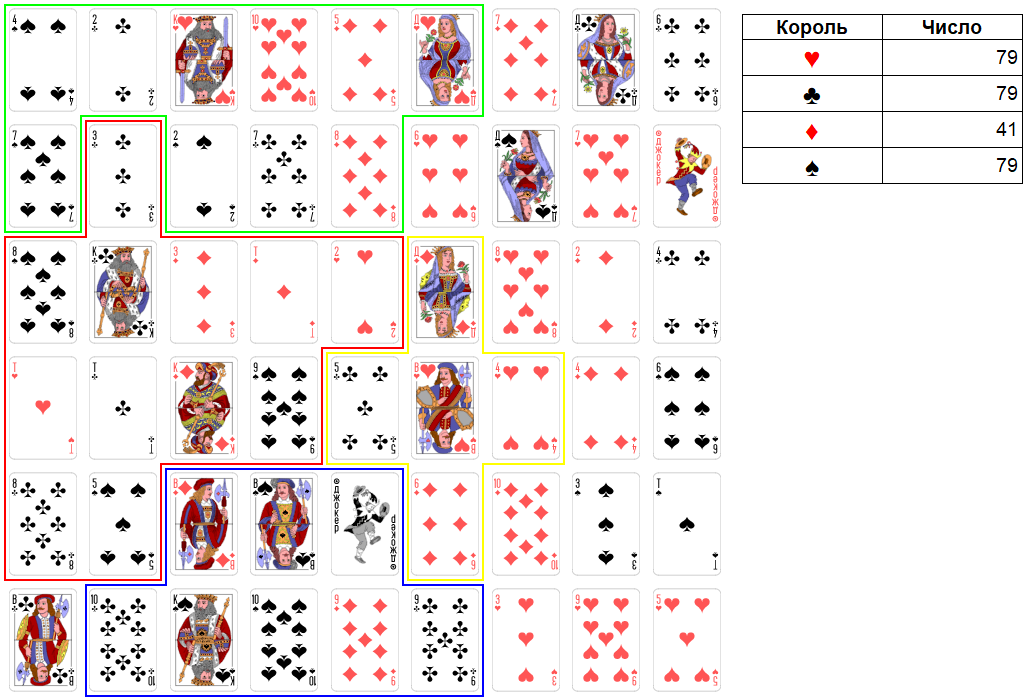
Рис. 18. Раунд 4. Ход короля бубен.

Ход короля виней. Максимально можно взять четыре карты достоинством: 5, 6, 11, 3. Итоговое число станет равно 104. Это слабое число. Имеет смысл не брать 5 крестей. Итоговое число будет равно 99. И король виней первым достигает этого очень сильного итогового числа.

 

 

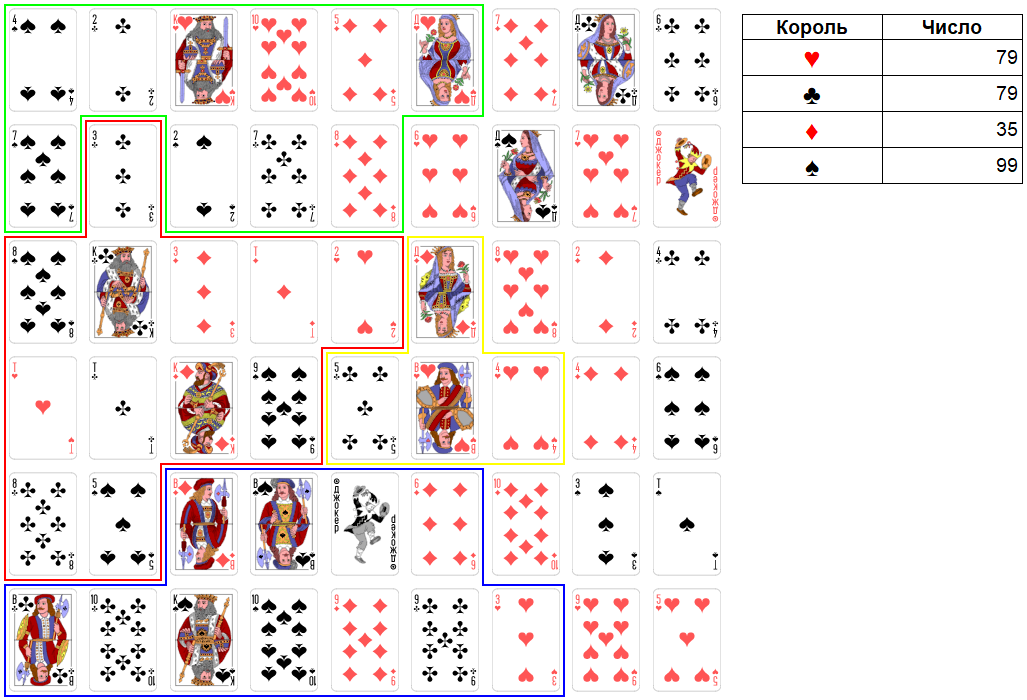
Рис. 19. Раунд 4. Ход короля виней.

 

Раунд 5.

Ход короля червей. Максимально можно взять две карты достоинством: 7, 6. Итоговое число станет равно 92. Это очень слабое число. Удача от короля червей отвернулась. В этой ситуации, возможно, ему имеет смысл не брать ничего. Но если посмотреть вперед, то можно увидеть, что его ближайший конкурент, король крестей, на своем следующем ходу возьмет даму бубен и 5 крестей, и будет иметь итоговое число, равное 99, так же, как и у короля виней. Поэтому ничего не брать это тоже не вариант. Король червей становится аутсайдером игры, и для него единственный вариант хоть что-то получить, это договариваться с другими королями. Поскольку ближайший сосед короля червей это король крестей (в союзе с королем бубен), то первому королю имеет смысл договориться со вторым. Договор будет таким. Король крестей набирает 99 очков и сдерживает дальнейшее расширение короля виней. А король червей тем самым расширяется под прикрытием короля крестей до итогового числа 199. После этого король червей и король крестей побеждают короля виней. Победу делят так. 1 / 4 победы (100 очков) достается королю червей, а 3 / 4 победы (300 очков) достается пополам королю крестей и королю бубен. Оба последних короля получат по 150 очков. После такого договора королю червей на текущем ходе имеет смысл взять только 7 бубен. Итоговое число станет равно 86.

 

 

Рис. 20. Раунд 5. Ход короля червей.

 

Ход короля крестей. Согласно договору с королем червей король крестей на этом ходе берет только даму бубен и 5 крестей, достигая итогового числа 99. Паритет с королем виней достигнут. Поскольку захвачена 5 крестей, территория короля бубен теперь будет управляться 4 червей.

 

 

Рис. 21. Раунд 5. Ход короля крестей.

 

Ход короля бубен. Максимально можно взять две карты достоинством: 4, 10. Итоговое число станет равно 29. Это сильное число. Но это не столь важно в рамках договоренности короля крестей и короля бубен, а также договоренности обоих этих королей с королем червей.

 

 

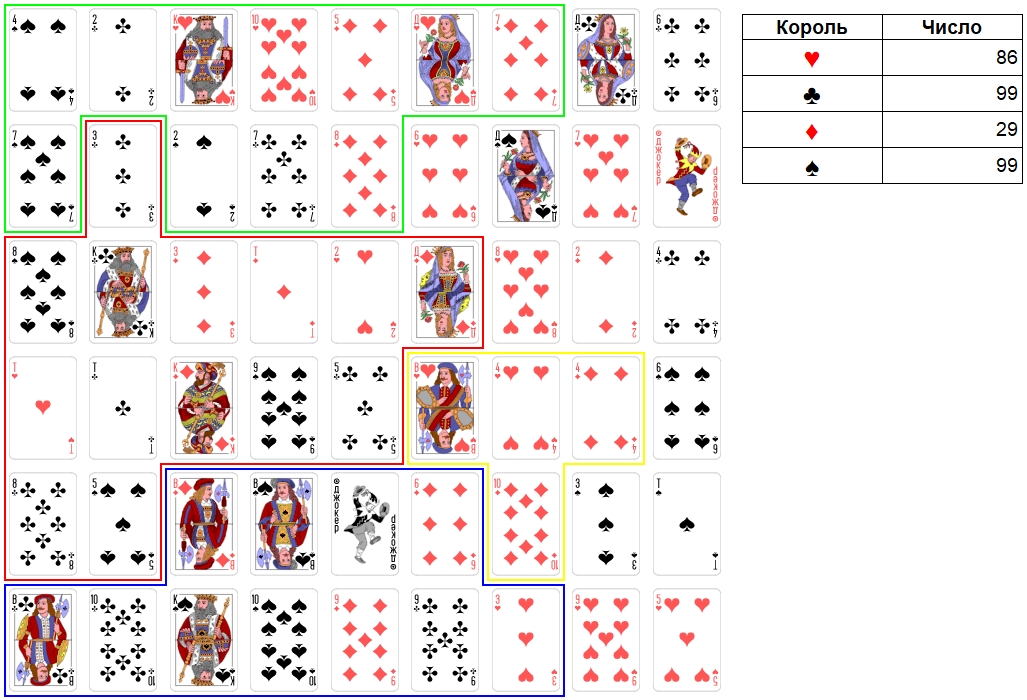
Рис. 22. Раунд 5. Ход короля бубен.

 

Ход короля виней. В силу выше написанной договоренности трех королей королю виней будет не сладко. Ему остается ждать. Возможно, план трех конкурентов короля виней не удастся. Во всяком случае, расширяться ему сейчас нельзя.

Раунд 6.

Ход короля червей. Король червей в рамках своей договоренности расширяется. Максимально можно взять три карты достоинством: 15, 6, 15. Итоговое число станет равно 122. Это очень слабое число. Имеет смысл не брать, например, даму крестей. В этом случае итоговое число будет равно 107.

 

 

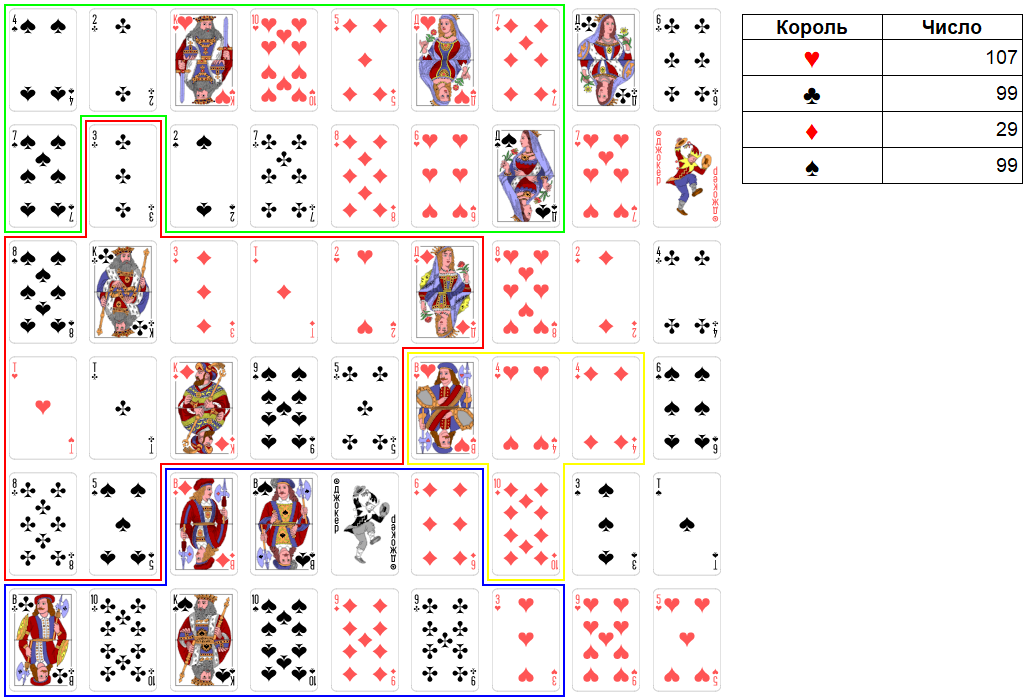
Рис. 23. Раунд 6. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход, сдерживая короля виней.

Ход короля бубен. Король бубен номинально расширяет свою территорию. Максимально можно взять четыре карты достоинством: 8, 2, 6, 3. Итоговое число станет равно 48. Это сильное число. Королю бубен главное не мешать расширяться королю червей. И он пока ему не мешает.

 

 

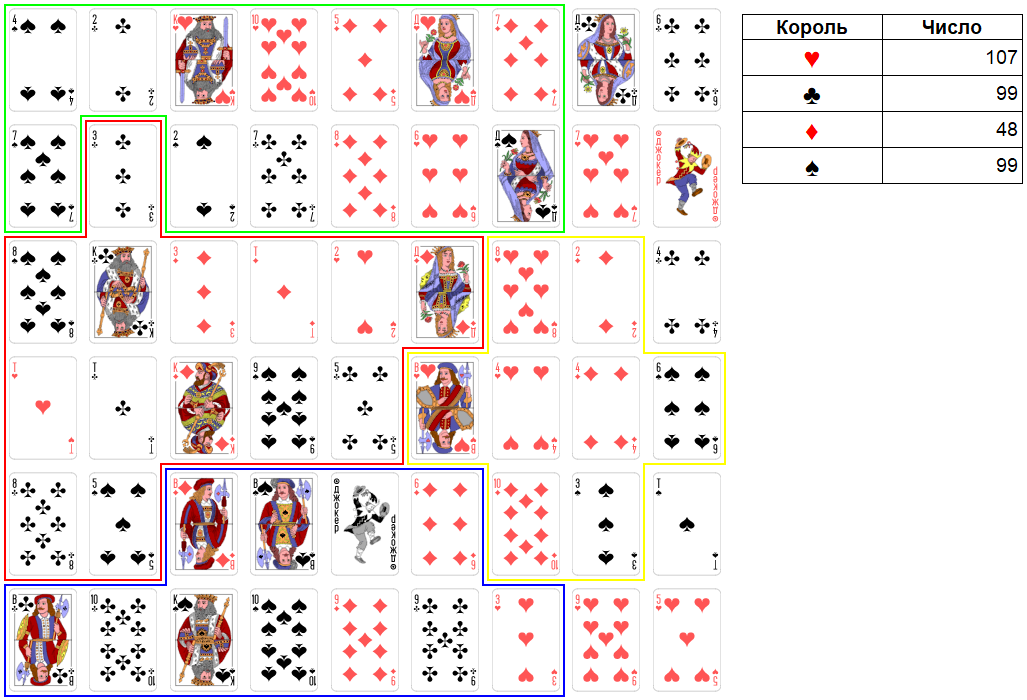
Рис. 24. Раунд 6. Ход короля бубен.

Ход короля виней. Король виней снова пропускает свой ход.

Раунд 7.

Ход короля червей. Максимально можно взять две карты достоинством: 15, 7. Итоговое число станет равно 129. Это сильное число.

 

 

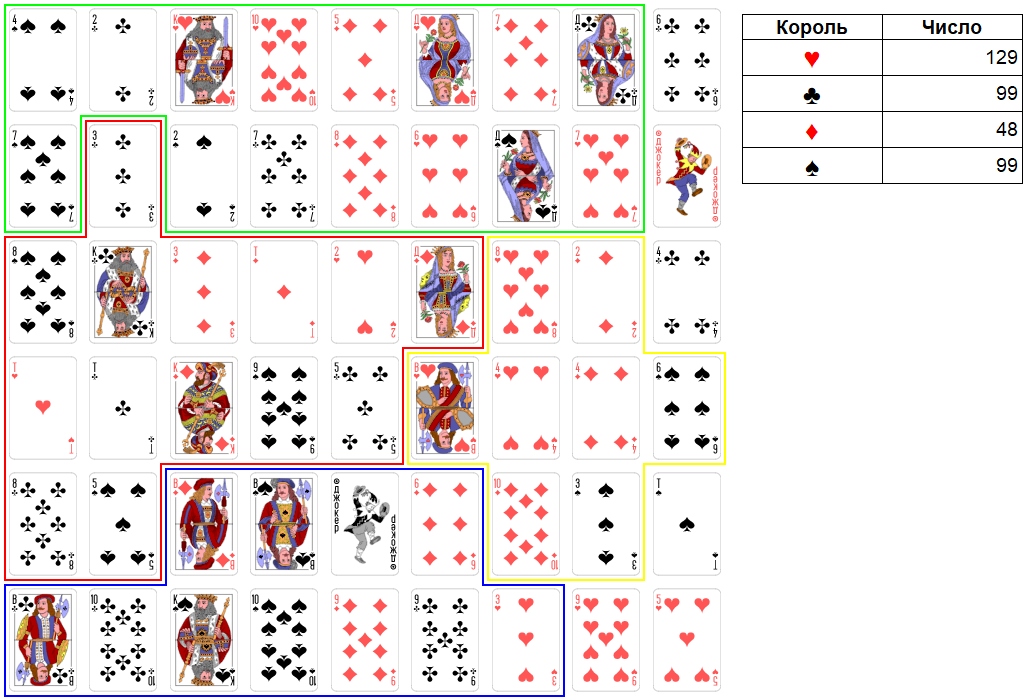
Рис. 25. Раунд 7. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Максимально можно взять две карты достоинством: 4, 1. Итоговое число станет равно 53. Это слабое число. В данном случае это хорошо, так как королю бубен сейчас нужно не мешать расширению короля червей, с которым у первого на двоих с королем крестей есть договоренность.

 

 

Рис. 26. Раунд 7. Ход короля бубен.

 

Ход короля виней. Король виней пропускает свой ход.

Раунд 8.

Ход короля червей. Максимально можно взять четыре карты достоинством: 6, 0, 8, 2. Итоговое число станет равно 145. Это не сильное число. Имеет смысл не торопиться и не брать пока 6 крестей. Итоговое число будет равно 139.

 

 

Рис. 27. Раунд 8. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Король бубен не может взять ничего и пропускает свой ход.

Ход короля виней. Король виней пропускает свой ход.

Раунд 9.

Ход короля червей. Максимально можно взять четыре карты достоинством: 6, 4, 4, 4. Итоговое число станет равно 157. Это сильное число. Но имеет смысл не торопиться и взять пока только 6 крестей и 4 бубен. Итоговое число будет равно 149.

 

 

Рис. 28. Раунд 9. Ход короля червей.

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Максимально можно взять две карты достоинством: 9, 5. Итоговое число станет равно 53. Это слабое число. Но это не важно.

 

 

Рис. 29. Раунд 9. Ход короля бубен.

 

Ход короля виней. Король виней пропускает свой ход.

Раунд 10.

Ход короля червей. Максимально можно взять четыре карты достоинством: 4, 4, 6, 3. Итоговое число станет равно 166. Это не сильное число. Имеет смысл не торопиться и взять пока только 4 червей и 6 виней. Итоговое число будет равно 159. Поскольку 4 червей захвачена, территория короля бубен будет управляться 3 виней.

 

 

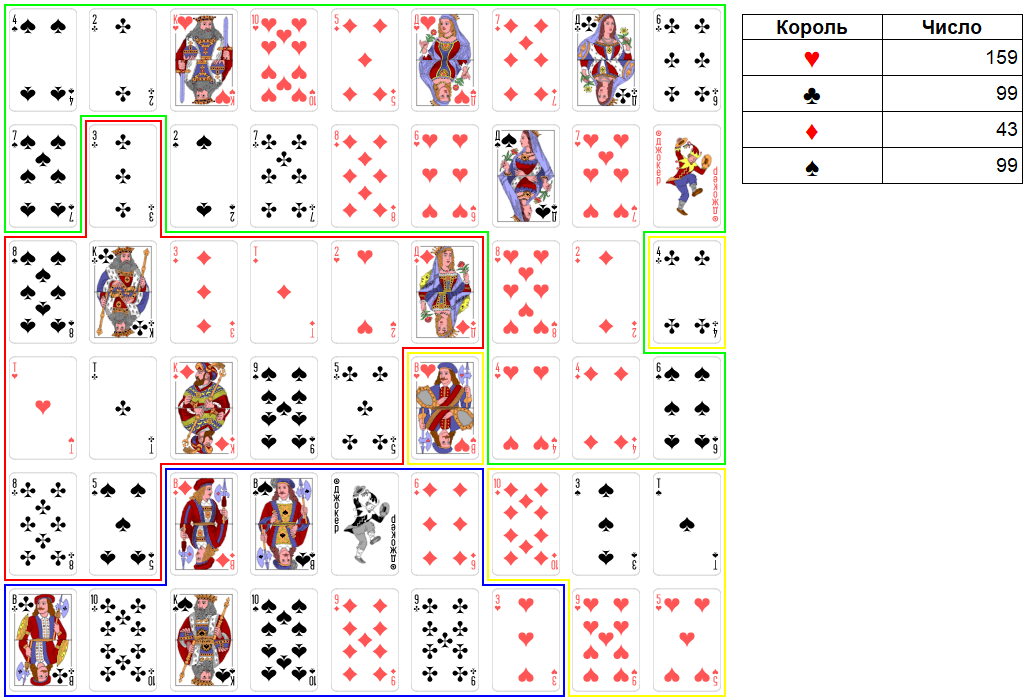
Рис. 30. Раунд 10. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Король бубен пропускает свой ход. Больше захватывать ему нечего.

Ход короля виней. Король виней пропускает свой ход.

Раунд 11.

Ход короля червей. Максимально можно взять пять карт. Итоговое число станет равно 188. Это сильное число. Но королю червей никак нельзя захватывать 3 виней. Ему нужно набрать 199 очков, для этого ему нужно захватить все карты у короля бубен кроме 3 виней. Расчет такой: 400 – 99 – 99 – 199 = 3. 3 очка нужно оставить. Поэтому на этом ходе он захватит только вальта червей, 10 бубен и туза виней. Итоговое число будет равно 181. Это очень слабое число. Но у короля бубен будет итоговое число еще слабее, равное 21. Поэтому дальнейшее расширение территории короля червей будет возможно. Территория короля червей теперь примыкает к территории короля виней.

 

 

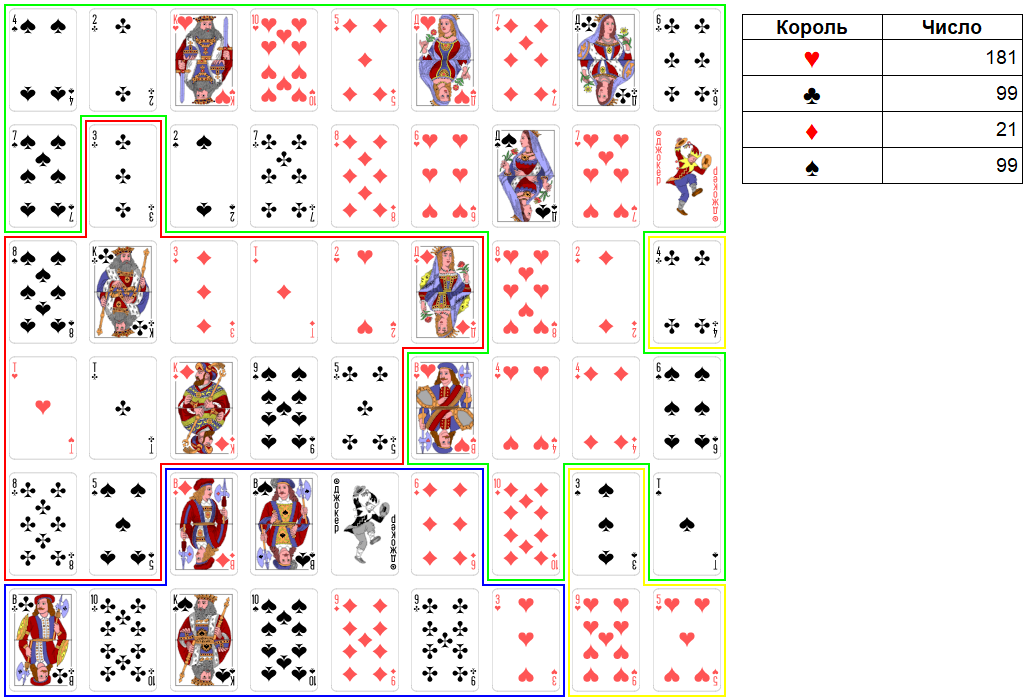
Рис. 31. Раунд 11. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Король бубен пропускает свой ход.

Ход короля виней. Король виней пропускает свой ход.

Раунд 12.

Ход короля червей. Максимально можно взять три карты достоинством: 4, 3, 5. Итоговое число станет равно 193. Это слабое число. Но, как было написано выше, королю червей никак нельзя захватывать 3 виней. На этом ходе он возьмет только 5 червей. Итоговое число будет равно 186.

 

 

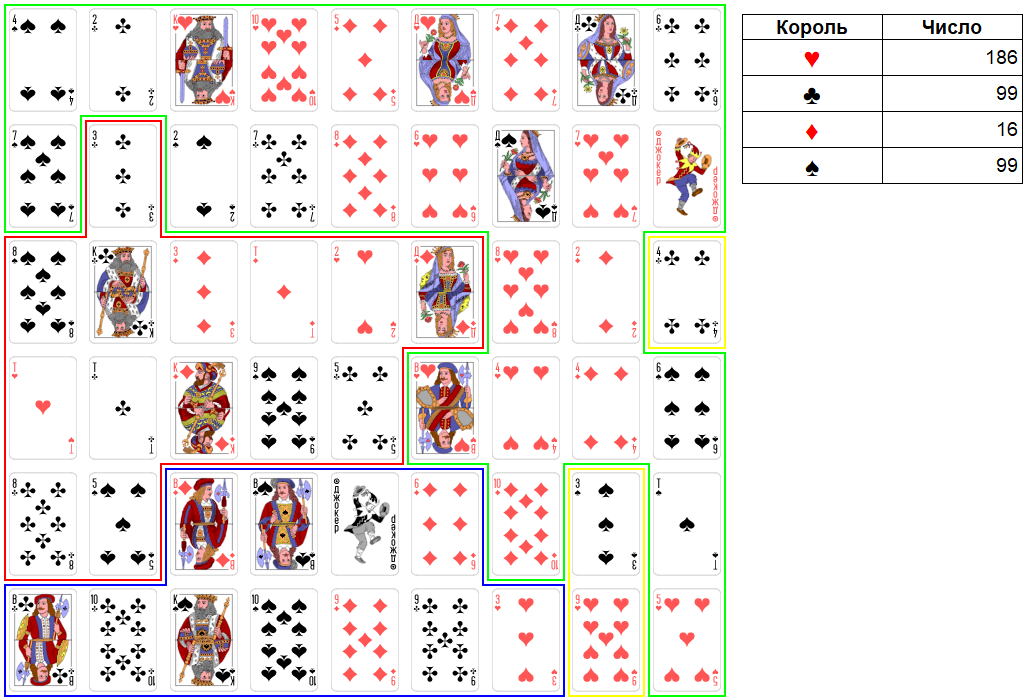
Рис. 32. Раунд 12. Ход короля червей.

 

Ход короля крестей. Король крестей пропускает свой ход.

Ход короля бубен. Король бубен пропускает свой ход.

Ход короля виней. Как видно, королю червей удается набрать 199 очков. На следующем ходе он возьмет 4 крестей и 9 червей и наберет нужное ему число. После этого нападение на короля виней будет возможно. Поэтому терять последнему нечего. Он начнет упреждающее наступление на короля червей. Максимально можно взять три карты достоинством: 11, 10, 9. Итоговое число станет равно 129. Это сильное число, хотя и много слабее, чем 99. Началась развязка.

 

 

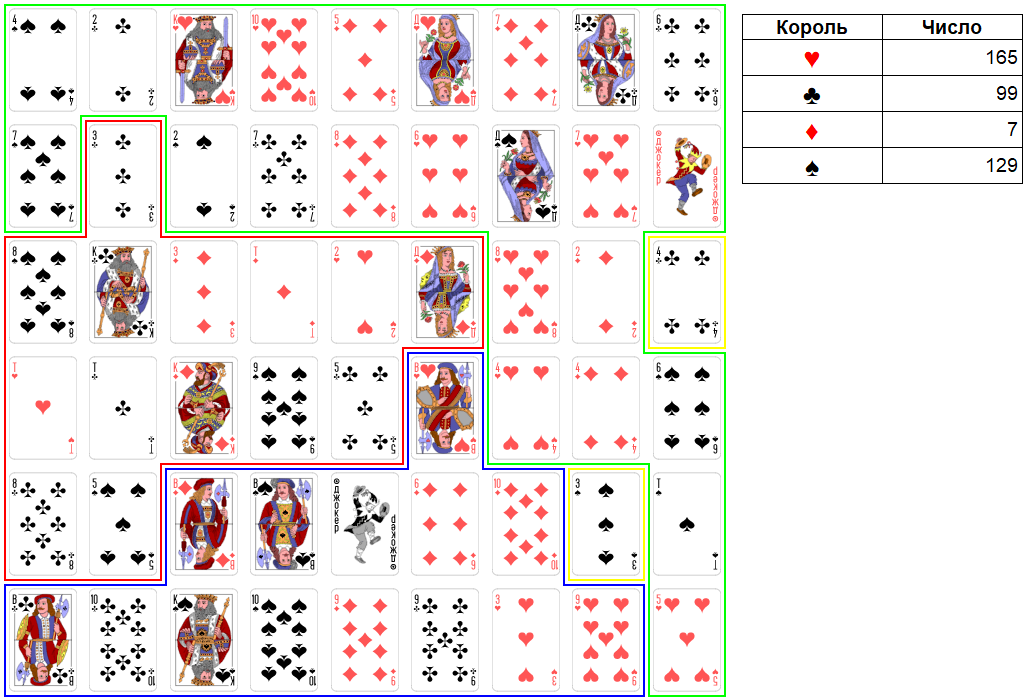
Рис. 33. Раунд 12. Ход короля виней.

 

Раунд 13.

Ход короля червей. Король червей ослабевает. Взять ему нечего. Он пропускает свой ход.

Ход короля крестей. Король крестей начинает массивное наступление на короля виней. Также он берет 6 червей у короля червей. Оба короля, король крестей и король червей, стали иметь сильное число 159.

 

 

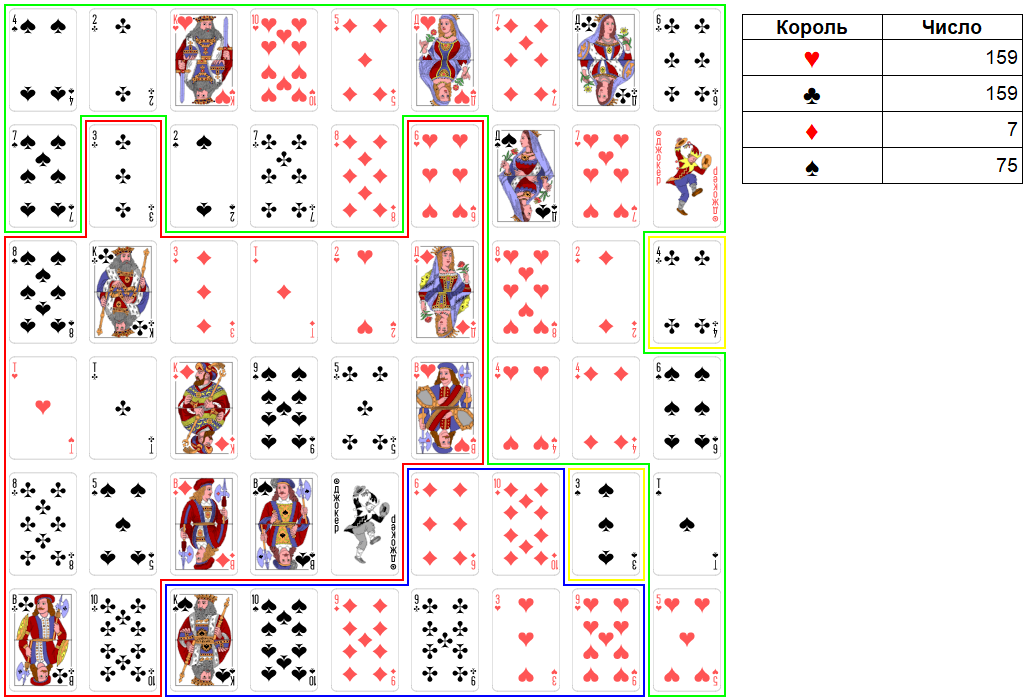
Рис. 34. Раунд 13. Ход короля крестей.

 

Ход короля бубен. Король бубен тоже начинает наступление на короля виней, захватывая у него 10 бубен.

 

 

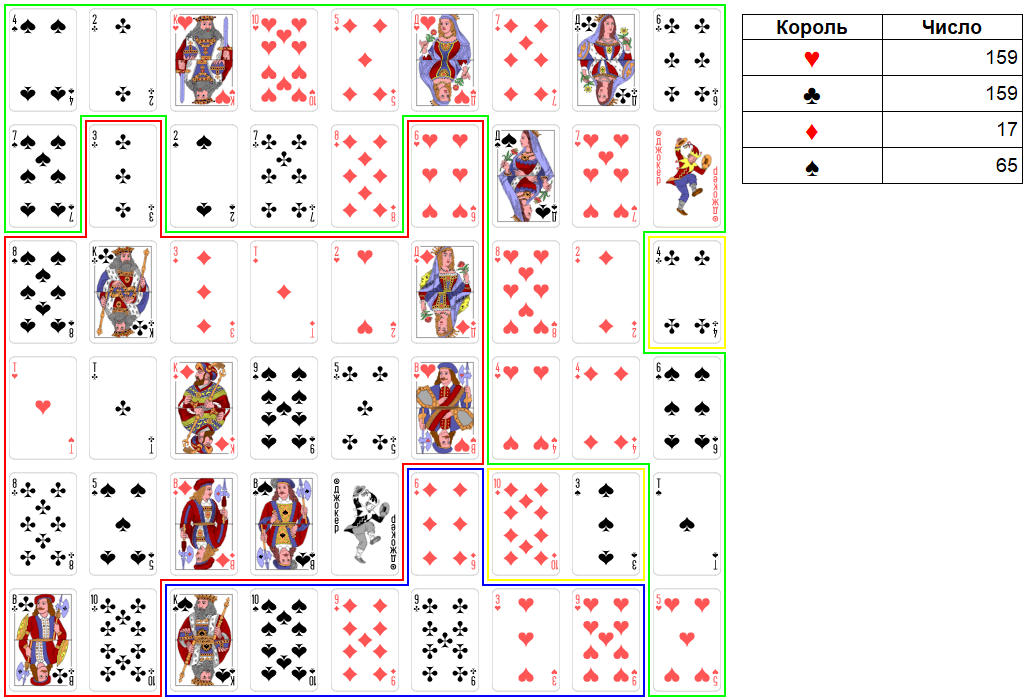
Рис. 35. Раунд 13. Ход короля бубен.

 

Ход короля виней. Король виней становится самым слабым из всех королей. Захватить ему нечего. Он пропускает ход.

Раунд 14.

Ход короля червей. Король червей пропускает свой ход, давая королю крестей и королю бубен захватывать территорию короля виней.

Ход короля крестей. Король крестей пока возьмет только 10 виней, набирая 169 очков.

 

 

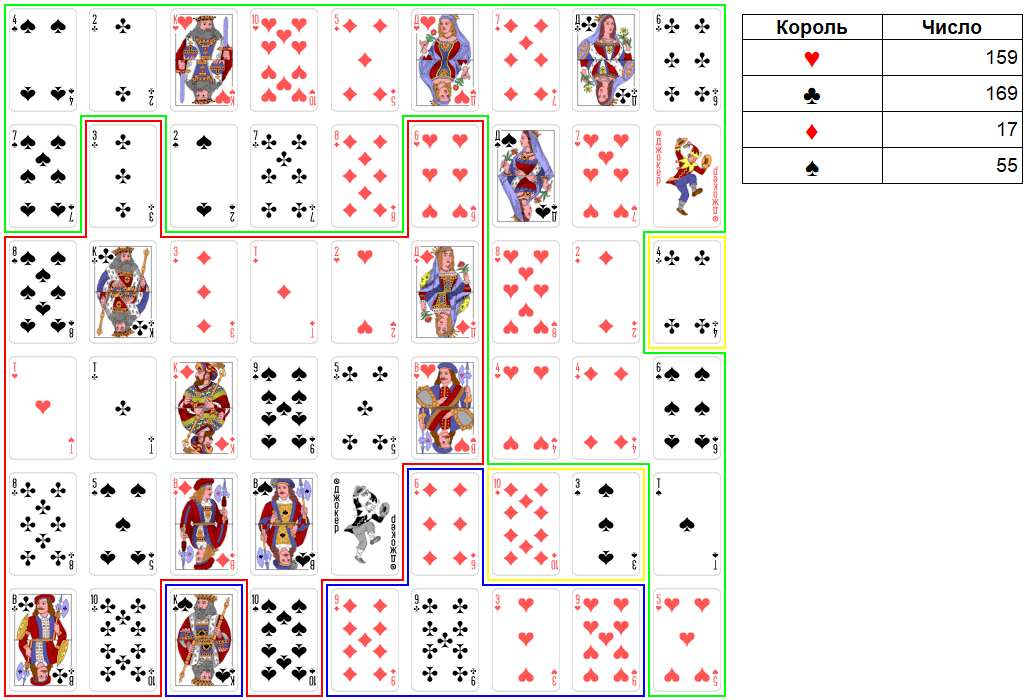
Рис. 36. Раунд 14. Ход короля крестей.

 

Ход короля бубен. Король бубен возьмет 3 червей и 9 червей, набирая 29 очков.

 

 

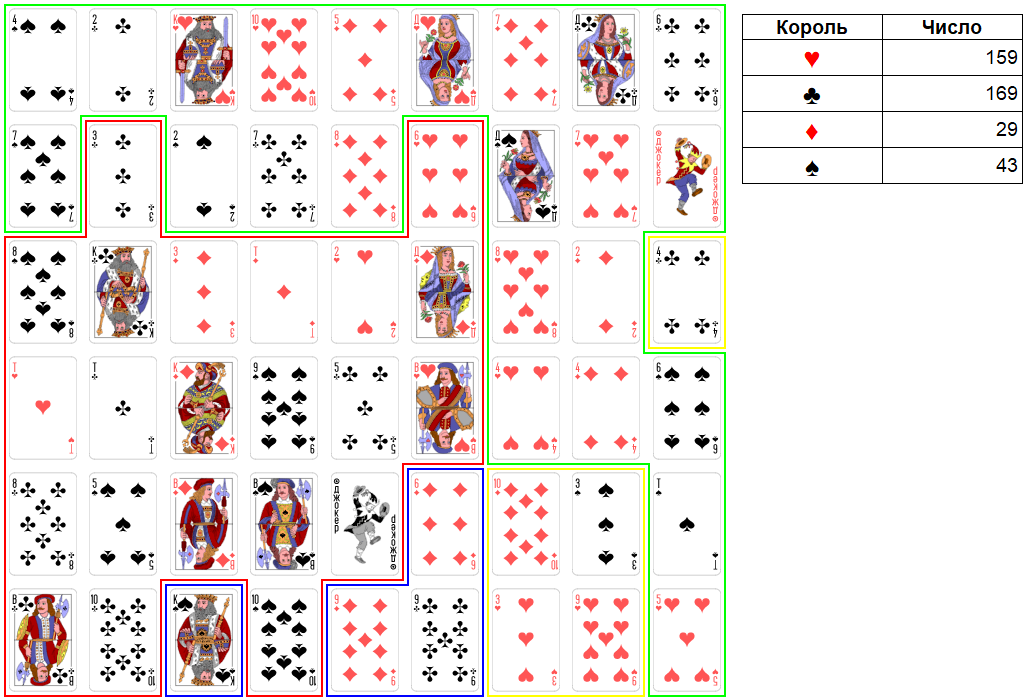
Рис. 37. Раунд 14. Ход короля бубен.

 

Ход короля виней. Король виней, очевидно, проигрывает эту игру.

После победы над королем виней остальные короли делят территорию согласно их договоренности: королю крестей и королю бубен по 150 очков, королю червей 100 очков.

 

 

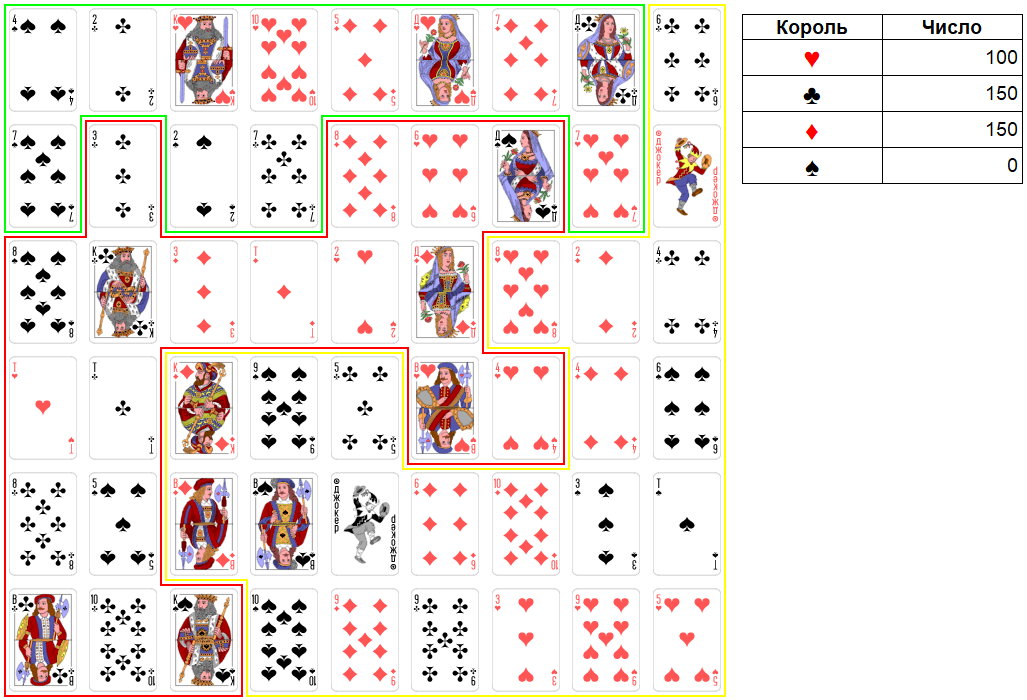
Рис. 38. Окончание игры.

 

Как уже понятно, игра «Короли» является одним из частных случаев игры «Империи», которую можно сделать для персонального компьютера, планшета или мобильного телефона. В общем случае размер игрового поля может быть произвольным. Например, приведем пример игры «Империи» с размером игрового поля 30х20:

 

 

Рис. 39. Территория империй на начало игры.

 

Количество клеток в данном примере игры будет соответственно равно 600. Правила, по которым при начале игры задаются числа для каждой клетки, могут быть разными. В нашем примере для каждой клетки число определялось случайным образом в интервале от 0 до 9 (только одноразрядные в десятичной системе числа).

Каждая из клеток может быть игроком, за которого играет человек или компьютер, т.е. быть империей, цель которой максимально расшириться. Естественно наибольший шанс на победу будет у тех игроков, клетка которых в начале игры имеет наиболее сильное число (в нашем примере это число 9).

В нашем примере за каждую из 600 клеток играет компьютер. Для расчета хода компьютера зашит определенный алгоритм. Каждая клетка-империя по очереди делает свой ход согласно данному алгоритму. Для демонстрации игры приведем территорию империй на начало 5 раунда:

 

 

Рис. 40. Территория империй на начало 5 раунда.

 

Как видно, из первоначальных 600 империй осталась на карте меньшая их часть, так как сильные империи при расширении захватывают слабые, включая их в свой состав.

Во всем остальном правила игры «Империи» аналогичны описанным выше правилам игры «Короли».

Выводы

1. Предложена игра «Империи», использующая математическое понятие фактическая заполненность разрядов чисел, в которую можно играть как с помощью игральных карт на столе, так и на персональном компьютере, планшете или мобильном телефоне.

2. Описана игра «Короли» для игральных карт, являющаяся частным случаем игры «Империи». Описаны возможные ее разновидности.

3. Приведен демонстративный пример партии в игру «Короли».

4. Предложен «женский» вариант игры «Короли» – игра «Дамы».

1. Харт А. Философское осмысление чисел в контексте их женственности и мужественности [Электронный ресурс] // Электронный периодический научный журнал «SCI-ARTICLE.RU». 2021. №10. С. 16-27. URL: https://sci-article.ru/number/10_2021.pdf (дата обращения: 17.03.2022).
2. Харт А. Абсолютная и фактическая заполненность разрядов чисел [Электронный ресурс] // Электронный периодический научный журнал «SCI-ARTICLE.RU». 2021. №11. С. 54-76. URL: https://sci-article.ru/number/11_2021.pdf (дата обращения: 17.03.2022).
3. Гик Е. Я. Занимательные математические игры. - 2-е изд., перераб. и доп. -М.: Знание, 1987. - 160 с.
4. Игры в карты. [Электронный ресурс] // URL: http://www.lightst.ru/card/games.htm (дата обращения: 17.03.2022).

Рецензии:

22.03.2022, 6:49 Мирмович Эдуард Григорьевич
Рецензия: Работа интересная, даже патентно значимая, предлагается в соответствующие её контенту разделы. Актуальность такого продукта может быть определена по количеству запросов на неё со стороны пользователей и потенциальных интересантов. Тонкая нить этой инструкции к игре связывает её с требованием научности. Однако где этот труд автора опубликовать в другом издании, предложить затруднительно. Рецензент, отмечая возможность публикации статьи, не может её рекомендовать, пока не будут усранены грамматические и синтаксические ошибки. Даже в аннтации автор не считается с правилами синтаксиса, не выделены причастные и другие обороты и пр. По самому описанию предлагаемой игры и нмного "притянутой за уши" теории чисел замечаний нет. После доработки в части устранения в тексте грамматических ошибок работа рекомендуется к печати в данном журнале.

23.03.2022, 15:25 Усов Геннадий Григорьевич
Рецензия: Настоящий журнал печатает статьи по НАУЧНЫМ направлениям. При этом необходимо в статьях указывать научную новизну работы. В этой статье научной новизны нет, поскольку об этом не сказал автор. В статье нет "математики", есть только отдельные числа и их сумма. Статья перегружена. Достаточно было указать в статье одну картинку - последнюю картинку, можно в небольшом размере, и данную игру, после ряда подсказок, каждый поймёт. Ведь покупая игру в "Детском мире", мы играем по инструкции к этой игре. А инструкция к игре должна быть на одну страницу! И незачем публиковать игральные карты, желая удивить читателей статьи. Можно было сказать о том, что если нет компьютера, то можно играть с помощью карт. Кстати, а почему только прямоугольник, а не произвольный "ступенчатый" плоский объект? И почему числа только до 10, а не до 35, 109, 287 и т.д.? Если в "Детском мире" покупается игра, то почему мы должны эту игру воспринимать как спорт? В силу вышесказанного данная статья не рекомендуется к печати в данном журнале.

2.06.2022, 10:11 Усов Геннадий Григорьевич
Рецензия: Автор статьи "долго, долго думал..." Он не ответил на мои конкретные вопросы, а попытался найти компромат в моих предыдущих статьях, причём в общем, не влезая в частности. По принципу: "сам дурак". Ещё один посетитель данного направления регулярно пользуется таким приёмом. И совсем непонятно, почему автор статьи не обратил внимание на 2 подсказки по приведению статьи в интересное сообщение. А то что автор статьи ссылается на предыдущего рецензента совсем плохо для этого АВТОРА: сталкивать двух реценцентов на "своём поле" - плохая идея.

15.08.2022, 10:18 Усов Геннадий Григорьевич
Рецензия: Мне совершенно не нравится эта статья. Автор показал, что с помощью данной игры три игрока, договариваясь, обыгрывают четвертого. При этом других вариантов быть не может. А эти три игрока как бы друг друга не знают. Это что-то напоминает ... Поэтому я против публикации такой статьи.



Комментарии пользователей:

6.07.2022, 0:45 Харт Алекс Отзыв: «Автор статьи "долго, долго думал..."» - И опять я долго, долго думал. Но не забыл. «Он не ответил на мои конкретные вопросы» - Надеюсь сейчас отвечу. «а попытался найти компромат в моих предыдущих статьях, причём в общем, не влезая в частности. По принципу: "сам дурак".» - Я лишь хотел показать, что Вас часто куда-то уносит не туда. Во время вашей рецензии возможно Вас тоже унесло куда-то не туда. Я до сих пор помню ваш ответ в одной из моих предыдущих статей. Вы написали 16.09.2021, 9:14: «(11) Как не понятно? Если есть новые символы в математике, то должны быть операции с этими символами: сложение, вычитание, умножение, деление, комплексные, действительные, и т.д. и т.п. Что будет, если разделить женственность на мужественность? Или взять мужественный корень из женственности? Да и что там мелочиться, осталось совсем немного: переписать всю наука "математика" на новый лад. А также смежные науки, где есть завязки с математикой.». «осталось совсем немного: переписать всю наука "математика" на новый лад.» - Что это было? Этот Ваш отзыв показал, что Вы совершенно не поняли смысла новых понятий, смысла статьи и Вас куда-то унесло не туда. Но не будем вспоминать прошлое. «Ещё один посетитель данного направления регулярно пользуется таким приёмом.» - Это не был прием. И я уж точно ни за кем не повторял. «И совсем непонятно, почему автор статьи не обратил внимание на 2 подсказки по приведению статьи в интересное сообщение.» - Это шутка такая? Или я должен был как-то прочитать Ваши мысли, чтобы понять Ваши подсказки? Или поиграть в угадайку? «А то что автор статьи ссылается на предыдущего рецензента совсем плохо для этого АВТОРА: сталкивать двух реценцентов на "своём поле" - плохая идея.» - Сталкивать цели не было. А вот показать в очередной раз, что Вы как всегда не в тренде, и что Вас куда-то унесло – это да. Ну давайте пройдемся по Вашим замечаниям. «Статья перегружена. Достаточно было указать в статье одну картинку - последнюю картинку, можно в небольшом размере, и данную игру, после ряда подсказок, каждый поймёт. Ведь покупая игру в "Детском мире", мы играем по инструкции к этой игре. А инструкция к игре должна быть на одну страницу!» - Блестяще. А сколько книг написано про шахматы? Не статей, а книг. Зачем? Достаточно в Википедии написать правила игры и все. Такая Ваша логика? А как показать красоту и захват игры? Только если действительно привести пример конкретной партии в эту игру с полным описанием интересных моментов в игре. «после ряда подсказок, каждый поймёт.» - Вы не уверен, что поймете. «И незачем публиковать игральные карты, желая удивить читателей статьи. Можно было сказать о том, что если нет компьютера, то можно играть с помощью карт.» - А что для компьютера уже вышла эта игра? Кроме того, предлагаемая игра «Империи» имеет разновидности. Для карт она своя. Частым случаем игры «Империи» является описываемая в статье игра «Короли» для карт. Почему нет? Боюсь, что сейчас Вы только с помощью карт и сможете поиграть в данную игру. «Кстати, а почему только прямоугольник, а не произвольный "ступенчатый" плоский объект? И почему числа только до 10, а не до 35, 109, 287 и т.д.?» - Блестяще. Это куда Вас опять понесло? Ваши вопросы можно адресовать и к игре в шахматы. А почему там именно 8 на 8, а не 9 на 9, 12 на 15, 17 на 104? А почему там квадратная доска, а не круглая, ступенчатая? А почему там есть король, а нет царя, императора, папы римского, маркизов, виконтов? Вы даете. Для игры «Короли», где 54 карты, оптимально делать поле 9*6. В целом не запрещено делать и другие поля. В статье же четко указано: «Как уже понятно, игра «Короли» является одним из частных случаев игры «Империи», которую можно сделать для персонального компьютера, планшета или мобильного телефона. В общем случае размер игрового поля может быть произвольным. Например, приведем пример игры «Империи» с размером игрового поля 30х20.». Написано же «размер игрового поля может быть произвольным». Именно для игры в «Короли» с помощью карт как оптимальный рекомендован именно вариант 9*6 как наиболее близкий к квадрату. Ничего удивительного в этом нет. «Если в "Детском мире" покупается игра, то почему мы должны эту игру воспринимать как спорт?» - Мы и шахматы можем купить в детском мире. Почему шахматы относят к спорту? И к Вашему удивлению есть даже спортивный покер. Представляете? Покупаете колоду карт, и уже занимаетесь спортом, играя в покер. Почему по такой же логике игра «Империи» не может быть отнесена к спорту? «В статье нет "математики", есть только отдельные числа и их сумма.» - А числа и сумма это не математика? Кроме того, не просто сумма, а применение нового математического понятия заполненность разрядов чисел. «Настоящий журнал печатает статьи по НАУЧНЫМ направлениям.» - Это единственный Ваш козырь. Слабенький козырь. Так, шестерка козырная. За неимением других аргументов Вы можете всегда использовать этот Ваш козырь, что в статье описана игра, а причем тут наука? «При этом необходимо в статьях указывать научную новизну работы. В этой статье научной новизны нет, поскольку об этом не сказал автор.» - Раздел «Научная новизна» в статье есть: «С появлением вычислительной техники появилось множество логических игр, основанных на числах. Игры же, основанной на таких свойствах чисел, как сила или слабость, которые описываются математическим понятием заполненность разрядов чисел, еще предложено не было.». В предыдущих статьях было дано математическое понятие «заполненность разрядов чисел». Но о конкретном его применении сказано мало. Поэтому, извините, показать применение этого понятия где-то актуально. Например, в предложенной математической игре. Поиграйте сами в эту игру с помощью игральных карт и поймете, что игра интересная. Вам понравится.

6.07.2022, 20:52 Усов Геннадий Григорьевич Отзыв: Автор статьи в половине комментария говорит не о статье, а о своём, личном. При этом оправдывается. Теперь о статье. «Для игры «Короли», где 54 карты, оптимально делать поле 9*6». А почему оптимально? Далее, говорится о большем количестве колод. А там какие поля? Вы принимаете то, что 49 сильнее, чем 129. Это противоречит законам математики. Вы продолжаете верить в сильные и слабые числа по своим правилам. Но это Вам флаг в руки. Тогда не говорите про математику. «…еще предложено не было.».Знаете, ещё много чего не было предложено. А нужно это предлагать? Для чего? В шахматах есть правила игры, а есть учебники по игре. Ваша статья о чём? То же самое и про покер. В учебнике по шахматам рассматриваются отдельные ходы, но нет полного рассмотрения партии, кроме очень интересных (чемпионат мира). У Вас рассматривается партия. Зачем? Можно остановиться на отдельных моментах. Ведь многие ходы из партии повторяются. Кстати, часто король пропускает ход. А почему, не сказано. «А что для компьютера уже вышла эта игра?» Так Вы сами сказали, что можно играть на компьютере. «Поиграйте сами в эту игру». Уже ясно, что в данном раскладе победит определённый король. В чём тогда соревнование???? В шахматах и в покере условия для игроков в начале игры одинаковые. У Вас условия уже разные из-за расклада.

6.07.2022, 20:55 Усов Геннадий Григорьевич Отзыв: Может быть Ваша игра создана только для того, чтобы оправдать Ваши новые "веяния" о силе определённых чисел?

7.07.2022, 14:58 Харт Алекс Отзыв: «Автор статьи в половине комментария говорит не о статье, а о своём, личном.» - Что конкретно там относится к «своему и личному»? «При этом оправдывается.» - Да нет. Просто показываю читателям, что Вы любите не разобравшись в материале куда-то уноситься. ««Для игры «Короли», где 54 карты, оптимально делать поле 9*6». А почему оптимально?» - Потому что поле наиболее близко к квадрату. Вы сейчас спросите, почему квадрат оптимален? Да? Вы прежде чем задавать вопросы сначала сами примените Ваши же вопросы на игре в шахматы. Почему там именно квадратное поле? Или давайте по-другому. Какой вариант поля как оптимальный предложили бы Вы при игре с 54 картами? «Далее, говорится о большем количестве колод. А там какие поля?» - В статье написано «если используется две колоды карт, то 12х9». Вы хотите, чтобы я расписал все оптимальные поля для игр с 3, 4, 5, 6 и т.д. колодами? Игра с 2 колодами уже будет достаточно долгой. И в ней могут принимать участие максимум 8 человек. Куда уж больше? Правило остается такое же. Желательно чтобы поле было максимально близко к квадрату. «Вы принимаете то, что 49 сильнее, чем 129. Это противоречит законам математики.» - Естественно противоречит. Вы же ранее писали, что надо для этого придумать другую математику. А если серьезно, то конечно же Вы до сих пор не разобрались в понятии заполненность разрядов, которое дано в предыдущих статьях. Никакого противоречия тут нет. В применении к игре «Короли». Территория каждого короля описывается числом. Чем больше число, тем больше масштаб империи короля. А сила империи определяется исходя из заполненности разрядов этого числа. Если сравнивать 49 и 129, то масштаб империи больше у второго числа. А сила больше у первого. Пример из жизни. В 19 веке Индия была в составе Великобритании. Но сравните население Индии и население Великобритании. Масштаб государства безусловно больше у Индии. А вот сила у Великобритании. (По реалиям 19 века.) Вот Вам и наглядный пример. Если описывать эти два государства одним числом, то 129 это Индия, а 49 – Великобритания. Самое интересно, что все это я уже объяснял Вам не раз в предыдущей статье. Пора бы уже приходить к пониманию. «Вы продолжаете верить в сильные и слабые числа по своим правилам. Но это Вам флаг в руки.» - Да это и не вера. Пифагорейцы тоже считали все нечетные числа мужскими, а четные – женскими. Понятие заполненность разрядов только подтверждает это для двоичной системы, о чем я писал Вам в предыдущей статье. Для Вас почему-то это слишком сложно понять. Хотя что там сложного? «Тогда не говорите про математику.» - Именно про математику и буду говорить, когда буду вспоминать понятие заполненность разрядов чисел. Я Вам даже как-то писал, что это некоторое расширение понятия остатка от деления. «Знаете, ещё много чего не было предложено. А нужно это предлагать? Для чего?» - Правильно. Для чего обезьяне превращаться в человека? Бананы сами растут. Ничего делать не надо. Лазай по деревьям, наслаждайся жизнью. Вот и все. Зачем что-либо предлагать? «В шахматах есть правила игры, а есть учебники по игре.» - В новой игре тоже есть правила. Только Вы у шахмат не спрашиваете, почему там правила именно такие, а у новой игры спрашиваете. Если новая игра будет в будущем популярна, то и по ней могут быть учебники. «Ваша статья о чём?» - Предложить математическую игру, в которой применяется понятие заполненность разрядов. Показать интерес, красоту и захват этой игры. «В учебнике по шахматам рассматриваются отдельные ходы, но нет полного рассмотрения партии, кроме очень интересных (чемпионат мира). У Вас рассматривается партия. Зачем? Можно остановиться на отдельных моментах. Ведь многие ходы из партии повторяются.» - Вы ознакомились с полной игрой. И мало что поняли. А что Вы поймете, если я остановлюсь только на отдельных моментах? Шахматы уже старая игра. Там нет смысла подробно рассматривать целиком партии. И то в некоторых случаях это рассматривается. Для новой же игры это более чем актуально. Как по-другому я должен показать весь интерес этой игры? Подскажите. «Кстати, часто король пропускает ход. А почему, не сказано.» - Сказано. Не внимательно читали. Какой конкретно пропуск хода Вам не понятен? «Так Вы сами сказали, что можно играть на компьютере.» - Да можно, если иметь соответствующую реализацию этой игры для компьютера. Пока что эта реализация есть только у меня. Вы путаете значения слова «можно». «Можно» в плане в принципе возможно, и «можно» в плане есть такая возможность уже сейчас. Уже сейчас такой возможности нет для большинства людей, но в принципе это возможно. Приходится Вам все разжевывать. «Уже ясно, что в данном раскладе победит определённый король. В чём тогда соревнование????» - Вы даете. В шахматах тоже понятно, что победит один из игроков или будет ничья. А заранее Вы можете сказать кто победит? Кто победит в игре изображенной на рис. 1? «В шахматах и в покере условия для игроков в начале игры одинаковые. У Вас условия уже разные из-за расклада.» - А в покере расклада нет? Там от случайности ничего не зависит, да? В шахматах кстати тоже условия не равны, потому что одни ходят первыми, другие вторыми. Так что абсолютной одинаковости условий нет ни в одной из перечисленных игр. «Может быть Ваша игра создана только для того, чтобы оправдать Ваши новые "веяния" о силе определённых чисел?» - А почему определенных чисел? Или Вы опять что-то не догоняете, что-то не поняли? Напомню, еще пифагорейцы делили числа на мужские и женские. Так что Вы не думайте, что я единственный кто говорит о силе и слабости чисел. Это уже объективная реальность. Для Вас это только до сих пор не понятно. Вы сперва поиграйте в игру «Короли», поймите весь ее интерес, а потом говорите. Во всяком случае думаю, что она поинтереснее покера. А то что она подтверждает актуальность использования понятия заполненность разрядов, это еще один плюс этой игры. Я играл в эту игру не раз, тестируя ее. И могу сказать, что она поинтереснее, чем игра в дурака, или в покер. Так что Геннадий Григорьевич, Вы не правы.

7.07.2022, 17:32 Усов Геннадий Григорьевич Отзыв: При раскладе, описанном в статье, король виней может победить? И что за такая договорённость о "разделе его имущества"?

7.07.2022, 23:51 Харт Алекс Отзыв: «При раскладе, описанном в статье, король виней может победить?» - Может. В точно таком же раскладе игроки могли сыграть и по-другому. И договоренности могли бы быть другими. Например, договор мог быть между королем виней и королем червей. «И что за такая договорённость о "разделе его имущества"?» - Примерно как раздел Речи Посполитой между Пруссией, Австрийской империей и Российской империей. В любой игре каждый игрок хочет победить и набрать наибольшее количество очков. В игре «Короли» победить в одиночку далеко не всегда возможно. Часто приходится договариваться двум королям о разделе территории других королей. В реальной жизни собственно также. Захватить весь мир не имея ни одного союзника это из области фантастики. А вот поделить мир между тройкой сильнейших держав уже более реальная задача.

8.07.2022, 7:24 Усов Геннадий Григорьевич Отзыв: "Может. В точно таком же раскладе игроки могли сыграть и по-другому." - А как по другому? Ведь Вы указали для каждого игрока оптимальное решение. Получается, что кто-то будет действовать не оптимально, то есть он не знает правила.

8.07.2022, 7:27 Усов Геннадий Григорьевич Отзыв: На мой взгляд, эта игра напоминает игру "Монополия", только на картах. Но там игроки не знают следующую фишку (карточка). Есть варианты. А здесь все фишки (карты) известны - получен расклад. Вариант здесь получается только один при оптимальных ходах.

8.07.2022, 7:28 Усов Геннадий Григорьевич Отзыв: "А вот поделить мир между тройкой сильнейших держав уже более реальная задача." - Это Ваше предложение на сегодня?

8.07.2022, 7:33 Усов Геннадий Григорьевич Отзыв: "В игре «Короли» победить в одиночку далеко не всегда возможно. Часто приходится договариваться двум королям о разделе территории других королей. " - А если не договорятся? На кулачки? А здесь какие правила? Об этом ни слова.

8.07.2022, 7:37 Усов Геннадий Григорьевич Отзыв: Странно. У короля виней не осталось карт, и его "державу" разбирают. При этом другие державы получают какие-то очки. Так откуда у короля виней много очков? Забирая карты, держава богатеет. А если у неё забирают карты, то держава должна беднеть.

9.07.2022, 0:41 Харт Алекс Отзыв: «На мой взгляд, эта игра напоминает игру "Монополия", только на картах. Но там игроки не знают следующую фишку (карточка). Есть варианты. А здесь все фишки (карты) известны - получен расклад. Вариант здесь получается только один при оптимальных ходах.» - См. выше. Оптимальных ходов может быть несколько. Особенно когда приходится с кем-то договариваться чтобы дальше расширять свою территорию, то обычно бывает как минимум два варианта с кем договариваться. А договор даже с одним королем можно заключить на разных условиях. Например, раздел 50 на 50, раздел 75 на 25, и т.д. Надо еще суметь договориться на больший для себя процент. Еще раз. Тезис, что после расклада все предопределено, не верен. Еще более он неверен при игре в закрытую, когда все карты сразу не видно (как на рис. 1). Они открываются только по мере расширения территории королей.

9.07.2022, 0:41 Харт Алекс Отзыв: «А как по другому? Ведь Вы указали для каждого игрока оптимальное решение. Получается, что кто-то будет действовать не оптимально, то есть он не знает правила.» - Я указал одно из оптимальных решений. При игре в шахматы если в начале игры сходить e2-e4, то это не будет самым оптимальным решением. Ход d2-d4 не менее хороший. В каких-то ситуациях как в игре «Короли» так и в игре «Шахматы» безусловно имеются единственные оптимальные ходы, но не во всех ситуациях так. Т.е. тезис, что после расклада карт уже все предопределено неверен. Кстати вернемся к шахматам. Вы же сами написали, что в шахматах имеется первоначальное равенство белых и черных. Белые ходят первыми. Но предположим, что это несущественное преимущество белых. Тогда, поскольку имеется первоначальное равенство, то отсюда вытекает, что если все будут ходить по Вашему оптимально, то по любому будет ничья. Только если кто-то не знает правил (как выразились Вы) и сделает неоптимальный ход, то будет не ничья, так?

9.07.2022, 0:41 Харт Алекс Отзыв: «"А вот поделить мир между тройкой сильнейших держав уже более реальная задача." - Это Ваше предложение на сегодня» - Конечно нет.

9.07.2022, 0:42 Харт Алекс Отзыв: «А если не договорятся? На кулачки? А здесь какие правила? Об этом ни слова.» - Ну почему сразу на кулачки. В статье написано: «Игра заканчивается, когда расширение империй королей больше не происходит.». Предположим никто ни с кем не стал договариваться. Т.е. каждый за себя. При этом есть варианты. Кто-то может рискнуть завоевать других королей в одиночку. Но это действительно риск. А если никто не стал рисковать. Каждый остался при своей территории. То расширения территорий больше не происходит, и игра окончена. При этом каждый получит очки как написано в статье: «Каждый игрок получает в конце игры количество очков, равное итоговому числу его империи.».

9.07.2022, 0:42 Харт Алекс Отзыв: «Странно. У короля виней не осталось карт, и его "державу" разбирают. При этом другие державы получают какие-то очки. Так откуда у короля виней много очков? Забирая карты, держава богатеет. А если у неё забирают карты, то держава должна беднеть.» - Подождите. Это где так, что у короля виней много очков? Рис. 35 – у короля виней 65 очков. Рис. 36 – 55, Рис. 37 – 43. Рис. 38 – 0. Где у короля виней много очков?

11.07.2022, 7:44 Усов Геннадий Григорьевич Отзыв: "После победы над королем виней остальные короли делят территорию согласно их договоренности: королю крестей и королю бубен по 150 очков, королю червей 100 очков." - Тогда откуда появились эти очки, если у короля виней 0 очков?

11.07.2022, 7:49 Усов Геннадий Григорьевич Отзыв: "После победы над королем виней остальные короли делят территорию согласно их договоренности: королю крестей и королю бубен по 150 очков, королю червей 100 очков." - Приведите пртокол договоренности. На каком шаге договоренности оги достигли согласие?

11.07.2022, 7:55 Усов Геннадий Григорьевич Отзыв: "Поскольку король бубен захвачен, его территория управляется из 5 крестей. Но напомним, что короли крестей и бубен, по сути, объединились и делят победу на двоих." - Захвачен или объединились? Если захвачен, то у короля бубей 0 очков.

11.07.2022, 7:57 Усов Геннадий Григорьевич Отзыв: "Рис. 38 – 0. Где у короля виней много очков?" - "После победы над королем виней остальные короли делят территорию согласно их договоренности: королю крестей и королю бубен по 150 очков, королю червей 100 очков." Какую территорию делят и по каким правилам? Откуда очки?

11.07.2022, 16:00 Усов Геннадий Григорьевич Отзыв: Самое главное: у тех участников, которые стартуют позднее (это "подтвердили" король бубей и король виней) мало шансов на выигрыш, так как предыдущие игроки уже получили дополнительные очки, а последующие игроки таких очков ещё не получили (ещё не было хода). И последующим игрокам сложно отбирать территории у предыдущих игроков.

12.07.2022, 1:28 Харт Алекс Отзыв: «На каком шаге договоренности оги достигли согласие?» - Раунд 2. Ход короля бубен. Договор между королем бубен и королем крестей делить выигрыш пополам. Раунд 5. Ход короля червей. Договор между королем червей и королями бубен и крестей. В статье написано: «Победу делят так. 1 / 4 победы (100 очков) достается королю червей, а 3 / 4 победы (300 очков) достается пополам королю крестей и королю бубен. Оба последних короля получат по 150 очков.». Небольшое пояснение. Если захватить все карты, то итоговое число, являющееся суммой всех карт, будет равно 400. В правилах игры об этом написано. Полная победа, это захват 400 очков. Поэтому при дележе 1 / 4 победы это 100 очков, 3 / 4 победы это 300 очков. Король бубен и король крестей договорились поделить победу пополам, т.е. из положенных им 300 очков каждый из них получит по 150 очков, о чем в статье и написано. Т.е. итого выигрыш делится так: король червей – 100, король бубен – 150, король крестей – 150. Итого 400 очков. «Приведите пртокол договоренности.» - Именно протокола нет, но в указанных выше раундах и ходах подробно описано, почему договорились, как договорились.

12.07.2022, 1:29 Харт Алекс Отзыв: «Тогда откуда появились эти очки, если у короля виней 0 очков?» - Договорившиеся короли делят не только территорию короля виней, но и незанятую никем территорию. По сути они делят всю карту между собой, все 400 очков. Когда у короля виней стало 0 очков, три короля в совокупности стали иметь 400 очков, но их надо поделить согласно договоренности: король червей – 100, король бубен – 150, король крестей – 150. Это и есть делёж победы между участниками договора.

12.07.2022, 1:31 Харт Алекс Отзыв: «Захвачен или объединились? Если захвачен, то у короля бубей 0 очков.» - Из рис. 13 видно, что король бубен вошёл в империю короля крестей. Не вся его территория, а только сама карта – король бубен. В этом смысле тут написано «захвачен». Этот «захват» произошел по согласию исходя из их договора. В рамках этого договора они объединились. 0 очков у него быть не может, потому что у него не вся территория захвачена. Из рис. 13 видно, что у него еще есть территория. Если угодно, захвачена его столица (по согласию конечно), но у него есть и еще территория. У него не 0 очков.

12.07.2022, 1:32 Харт Алекс Отзыв: «"После победы над королем виней остальные короли делят территорию согласно их договоренности: королю крестей и королю бубен по 150 очков, королю червей 100 очков." Какую территорию делят и по каким правилам? Откуда очки?» - В предыдущих ответах надеюсь я дал ответ на этот вопрос. Территория здесь – это всё поле, все 54 карты, общей суммой в 400 очков. Это и есть очки, которые делят. По правилам исходя из их договоренности: 100 + 150 + 150 = 400.

12.07.2022, 1:35 Харт Алекс Отзыв: «Самое главное: у тех участников, которые стартуют позднее (это "подтвердили" король бубей и король виней) мало шансов на выигрыш, так как предыдущие игроки уже получили дополнительные очки, а последующие игроки таких очков ещё не получили (ещё не было хода). И последующим игрокам сложно отбирать территории у предыдущих игроков.» - Вот это уже хорошее наблюдение. Если более точно, то можно выделить два фактора влияющие на вероятность победы. 1) Очередность хода, 2) Расположение короля. Кто ходит 1-ым у того преимущество. И кто ближе к центру поля у того преимущество. Поэтому справедливо определить ходы так, чем ближе король к краю (точнее к углу), тем очередность его хода должна быть раньше. Но это по желанию. Это не обязательное правило. В статье написано, что порядок ходов в целом может быть любым: «4. Определяется порядок ходов королей. Он может быть произвольным. Например, порядок может определяться исходя из расположения королей, слева направо и сверху вниз (как чтение текста).». Но из вышесказанного не следует, что король, находящийся у края и ходящий последним, обязательно проиграет. Вы пишете «это "подтвердили" король бубей и король виней». Как раз по этой игре это не подтверждено. Во всяком случае на примере короля виней, который находится с краю и ходит последним. Из рис. 19 видно, что король виней первым достигает сильного числа 99. Проиграл он лишь из-за договоренности остальных королей против него. Могла быть и другая договоренность. Договоренность могла быть трех королей против короля червей. Хотя в целом Вы правы. Ходить первым лучше, чем последним. Есть еще один фактор – расположение поблизости других королей. Если два короля слишком близко друг к другу, то высока вероятность, что один из них захватит другого вначале игры. Факторов много. Это и есть игра. Например, если играть в дурака, то после раздачи карт можно сразу оценить вероятность победы. Если у Вас на руках в начале игры будут козырные туз, король, дама, валет, то на Вашем лице можно будет увидеть излучение радости. А если у Вас на руках не будет ни одного козыря, будут только лишь одни слабые карты, то едва ли можно будет увидеть радость на Вашем лице. Возвращаясь к теме очередности хода. Чтобы как-то нивелировать этот фактор можно определять очередность хода исходя из расположения королей, как я написал выше.

12.07.2022, 8:53 Усов Геннадий Григорьевич Отзыв: Если что-то не так в Вашей игре, то у Вас появляется фраза -"Могла быть и другая договоренность." Найдите мне игры, где в процессе игры появляются новые договорённости между игроками, которые меняют соотношение очков, вистов, голов и ещё чего-нибудь. А на кону победа, успех, иногда - деньги. У Вас слишком много договорённостей. И последняя договорённость в конце игры: стороны набрали очки, а затем они решили ????, что кто-то может получить меньше, а кто-то получить больше.

12.07.2022, 8:57 Усов Геннадий Григорьевич Отзыв: Скажите: а чем хуже король виней по сравнению с королем бубей? Первый ничего не получил, а второй - хотя всё потерял (то ли захватили, то ли объединили), тем не менее даже получил очень много очков (и снова - по непонятной договорённости).

12.07.2022, 9:57 Усов Геннадий Григорьевич Отзыв: Что-то у Вас всё тянет на мужское-женское: Дамы и Короли. А почему не может быть юношеский вариант: Валет?

13.07.2022, 1:02 Харт Алекс Отзыв: «Если что-то не так в Вашей игре, то у Вас появляется фраза -"Могла быть и другая договоренность."» - Вы пока так и не показали, что не так в предлагаемой игре. Я много раз сам играл в эту игру тестируя ее. И скажу, что здесь одна партия интереснее другой. А Вы говорите, что что-то не так. «Найдите мне игры, где в процессе игры появляются новые договорённости между игроками, которые меняют соотношение очков, вистов, голов и ещё чего-нибудь. А на кону победа, успех, иногда - деньги.» - Конечно не так много вообще есть игр, где вообще есть договоренности между игроками. Обычно каждый за себя. Но вот пример. Игра «Конкурент». Это некий аналог игр «Менеджер», «Монополия». Там есть правило: «Обмен карточками Отросли предприятий ведется на договорных условиях между игроками.». Т.е. игроки могут договориться как угодно. А на кону победа, успех, иногда – деньги, как Вы выражаетесь. В игре «Короли» тоже есть договоренности между королями. В реальной жизни есть союзы, двусторонние договоры между государствами. То же самое и в игре «Короли». Эта игра – некоторая модель расширения королевств, превращения их в империи. От феодальной раздробленности, когда практически нет государства и до образования огромной империи. Договоренности между разными государствами были всегда. А на кону территория государства, богатство нации, а иногда и существование государства. «У Вас слишком много договорённостей.» - В этой описываемой в статье партии только две договоренности. Это много? В других партиях может быть одна договоренность, или ни одной. Сколько будет договоренностей, зависит от самих участников. Я уже писал, что в идеале каждый король хочет завоевать победу в одиночку, и тогда не нужны никакие договоры, и не надо ни с кем делиться очками. Беда в том, что в одиночку очень сложно победить других игроков, стать единственным победителем в игре и получить 400 очков. «И последняя договорённость в конце игры: стороны набрали очки, а затем они решили ????, что кто-то может получить меньше, а кто-то получить больше.» - Эта договоренность о том кто сколько получит была не в конце игры. Короли бубей и крестей договорились, что получат поровну, почти вначале игры. Потом к ним присоединился и король червей. Исходя из их договоренности они и получили свои очки в конце игры. В чем здесь проблема? Всё честно.

13.07.2022, 1:06 Харт Алекс Отзыв: «Скажите: а чем хуже король виней по сравнению с королем бубей? Первый ничего не получил, а второй - хотя всё потерял (то ли захватили, то ли объединили), тем не менее даже получил очень много очков (и снова - по непонятной договорённости).» - Почему договоренность непонятная? Написал Вам на каком ходе договорились, почему договорились. Вопрос "чем король виней хуже» не корректен. Представьте, Вы играете в дурака и проигрываете. И спрашиваете: «Чем я хуже?» Ну наверное или совершили ошибку в игре, или всю игру шли плохие карты, мало козырей. Есть объективные причины проигрыша. Они есть также и у проигрыша короля виней. Могла игра идти по-другому? Да могла. Также как и Вы в упомянутой гипотетической игре в дурака, если бы играли немного по-другому, то могли и выиграть. Я например могу написать одну из оплошностей короля виней приведшей к проигрышу. Как только короли крестей и бубей договорились, надо было сразу постараться договориться с королем червей. И было бы двое на двое. А король виней такого союза не предложил. Он был самым сильным и думал, что в одиночку сможет победить всех. Это оказалось ошибкой. Вот Вам одна из причин проигрыша короля виней. Я уже писал, что данный расклад, который описан в игре, имеет множество вариантов того, как будет развиваться игра. Описан лишь один из них, более менее вероятный.

13.07.2022, 1:09 Харт Алекс Отзыв: «Что-то у Вас всё тянет на мужское-женское: Дамы и Короли. А почему не может быть юношеский вариант: Валет?» - Игра «Короли» или «Дамы» как Вы понимаете, это частный случай игры «Империи». Вариаций игры может быть бесконечно много. Вы также можете спросить, а почему в игре «Короли» валет 11 очков, дама 15, а король 19? Конечно можно этим картам приписать любые очки. Я подгонял значения карт так, чтобы сумма итого по масти была равна 100 очкам. Но такие вопросы из разряда, почему правила игры именно такие. А почему в шахматах конь стоит ближе к углу, чем слон? Вы спрашиваете «А почему не может быть юношеский вариант: Валет?». Может. Всё может. Но по смыслу игры – расширение территории государств – во главе государства конечно король. (Надеюсь не спросите, а почему не президент?) Поэтому и игра «Короли». Как женский вариант предложен вариант «Дамы». На этом остановился. Даже вариация игры «Дамы» возможно излишняя. Достаточно игры «Короли». Вариация игры «Вальты» на мой взгляд тем более излишняя. Хотя возможна.

17.07.2022, 10:52 Усов Геннадий Григорьевич Отзыв: "Поэтому имеет смысл брать только туза и короля. ... Король крестей догоняет в силе своего основного конкурента – короля виней. Поскольку король бубен захвачен, его территория управляется из 5 крестей. Но напомним, что короли крестей и бубен, по сути, объединились и делят победу на двоих." Вы себе противоречите: Вы можете спокойно забрать короля бубей и ещё что-нибудь, что Вы делаете. А далее Вы почему-то соглашаетесь объединиться с королём бубей и поделить получаемые очки.

17.07.2022, 10:56 Усов Геннадий Григорьевич Отзыв: "Ход короля виней. В силу выше написанной договоренности трех королей королю виней будет не сладко. Ему остается ждать. Возможно, план трех конкурентов короля виней не удастся. Во всяком случае, расширяться ему сейчас нельзя." - Вы не объяснили: почему нельзя королю виней расширяться.

18.07.2022, 0:29 Харт Алекс Отзыв: «Вы себе противоречите: Вы можете спокойно забрать короля бубей и ещё что-нибудь, что Вы делаете. А далее Вы почему-то соглашаетесь объединиться с королём бубей и поделить получаемые очки.» - А Вы логическую нить не потеряли? Почитайте крайне внимательно «Раунд 2. Ход короля бубен.». Там четко написано о договоренности короля крестей и короля бубей. Если я потом пишу, что король бубей захвачен, то как Вы думаете, что это значит в контексте вышеприведенной договоренности? Итак. Короли бубей и крестей объединились. Договорились делить победу пополам еще на 2-ром раунде игры. И в конце игры это и случилось. Если есть потом слова «король бубей захвачен» это просто как констатация факта, что его столицы нет, и нужно выбрать другую для управления его территорией. Сам же захват произошел по согласию с королем крестей. Кто захватил? Король крестей. И уже после их договоренности. Там же написано четко: «Король бубен захватывает сейчас максимальное количество карт, тем самым, ослабляя себя и позволяя королю крестей брать его карты на следующем ходе, усиливая себя.». Видите? «позволяя королю крестей брать его карты». Вот он и взял его столицу. По договоренности. Победа пополам уже обеспечена королю бубей. Если конечно они оба победят. В чем противоречие?

18.07.2022, 0:30 Харт Алекс Отзыв: «Вы не объяснили: почему нельзя королю виней расширяться.» - Возможно Вам не понятно, потому что Вы так и не поняли как определяется сила того или иного короля. Из рис. 22 видно, что у короля виней и короля крестей у обоих по 99 очков. Это очень сильное число: две девятки в конце. Число более сильное чем 99 ближайшее это 199. Т.е. через 100 очков. Сразу 100 очков набрать за один ход нереально. Это собственно и видно из рис. 22. Король виней максимум может взять за ход 30 очков: вальта червей, 10 бубей, 9 червей. Т.е. при любом взятии комбинации из этих 3-х карт он неизбежно ослабевает. И король крестей совершенно спокойно на следующем ходе может на него напасть. А если ничего не брать, то король виней остается при сильном числе 99. В «Раунде 5. Ход короля червей.» написано некоторое пояснение этому: «Договор будет таким. Король крестей набирает 99 очков и сдерживает дальнейшее расширение короля виней. А король червей тем самым расширяется под прикрытием короля крестей до итогового числа 199.» Боюсь это Вам тоже не понятно. «сдерживает дальнейшее расширение» - у обоих королей по 99 очков – очень сильное число. Оба расширяться не могут, так как ослабнут. И у них паритет. Это и есть «сдерживает расширение короля виней». Ему расширяться нельзя, потому что он неизбежно ослабевает и его захватывают. Так то конечно он расширяться может, но это будет глупым ходом.

18.07.2022, 16:39 Усов Геннадий Григорьевич Отзыв: Я не поддерживаю игры, где 3 участника объединяются против одного участника. Согласно правилам игры после договорённостей в 5 раунде можно останавливать игру. Так как один из 3-х участников всегда наберет 199 очков, то есть вооружается, пока остальные сдерживают 4-го участникаю Об этом надо было сказать.

18.07.2022, 16:45 Усов Геннадий Григорьевич Отзыв: Вы вводите понятие сильного числа по своим правилам. Найдите мне закон по математике такой, чтобы выполнялось это условие силы. Раз не найдёте, значит, эти сильные числа не относятся к математике, значит, статью нельзя публиковать под разделом "Математика".

18.07.2022, 18:09 Усов Геннадий Григорьевич Отзыв: Чтобы были равные условия у участников, необходимо их королей развести, например, по углам, или по сторонам. А далее поля заполняются с помощью сдачи.

19.07.2022, 0:14 Харт Алекс Отзыв: «Вы вводите понятие сильного числа по своим правилам. Найдите мне закон по математике такой, чтобы выполнялось это условие силы. Раз не найдёте, значит, эти сильные числа не относятся к математике, значит, статью нельзя публиковать под разделом "Математика".» - В статье написано «В данной игре используется математическое понятие фактическая заполненность разрядов чисел, которое определено в работах [1] и [2].». В этих работах введено понятие фактическая заполненность разрядов. Очевидно, это относится к разделу «Математика». Что здесь не так? В игре каждая империя описывается определенным числом. Величина этого числа определяет масштаб империи. А фактическая заполненность этого числа определяет силу империи. Что здесь не так? Какой конкретно закон в математике Вы хотите увидеть? Я не могу дать новое определение чего-то в математике? Не могу использовать это понятие для описания чего-то? Напомню, что заполненность разрядов чисел в двоичной системе может быть использовано для описания мужественности и женственности. Если мужественность и женственность рассматривать исключительно в контексте силы, то мужественное это сильное, а женственное – слабое. Что здесь не так?

19.07.2022, 0:14 Харт Алекс Отзыв: «Чтобы были равные условия у участников, необходимо их королей развести, например, по углам, или по сторонам.» - Да, это возможно. Абсолютно равными условия не станут, так как все равно кто-то ходит первым, кто-то вторым и т.д. Но тем не менее. «А далее поля заполняются с помощью сдачи.» - Такой вариант эквивалентен игре «в закрытую» (как на рис. 1). (Вообще основным вариантом игры «Короли» является вариант именно «в закрытую», когда не видно, какие карты где лежат. Они открываются только по мере их захвата королями.) Если я правильно понял Ваше «с помощью сдачи».

19.07.2022, 0:19 Харт Алекс Отзыв: «Я не поддерживаю игры, где 3 участника объединяются против одного участника.» - Я уже писал, что в идеале каждый хочет победить в одиночку и получить все 400 очков, а не часть из них. Беда в том, что далеко не всегда это возможно. И всегда есть риск, что не получится. По Вашему три короля объединились против четвертого от нечего делать? Они ведь в итоге получили каждый 150, 150 и 100 очков. 400 никто не получил. Они объединились, потому что в одиночку победить не могут. (Напомню, что договоренности могли быть и другие.) Представьте, что играет 1000 человек в игру «Короли». Максимально можно набрать 100000 очков. И вот 999 королей объединились против одного. Естественно они его легко выиграют. Но каждый получит по 100000 / 999 очков, что примерно равно 100. Т.е. да, круто, они победили, но им мало дадут очков. А представьте, что победил один король без договоренностей. То он получит все 100000 очков. Договоренности делаются не от нечего делать против кого-то одного, а из необходимости. По другому выиграть не получается. Помню в детстве играли в игру по-моему в «Лапту» (может и по другому называется эта игра). И там вроде бы кидают палку. И бывает, что кого-то одного замаят. И Вы скажете: «я не поддерживаю игры, где вот так маят одного игрока». Это игра. Бывает. Кроме того, я писал Вам, что король виней совершил ошибку, что сам заблаговременно не договорился с королем червей. Бывает. Совершил ошибку. Проиграл. По одной партии судить не стоит. В других партиях уже может быть так, что нет вообще ни с кем договоренностей, или договоренность двое на двое. Всякое может быть. Это лишь один из примеров игры в «Короли». «Согласно правилам игры после договорённостей в 5 раунде можно останавливать игру. Так как один из 3-х участников всегда наберет 199 очков, то есть вооружается, пока остальные сдерживают 4-го участникаю» - Это не совсем так. У короля виней 99 очков. Его сдерживает король крестей – у него тоже 99 очков. Из 400 остается 400 – 99 – 99 = 202. Надо набрать 199. Т.е. надо не брать 3 очка. А что если все 3-ки уже взяли (королем крестей или виней). Кроме того, взяли все тузы (1 очко). Получается никак нельзя набрать 199 очков при таком раскладе. Даже если и «игру можно останавливать», в чем здесь проблема? Например, игра в шахматы. Один зевнул ладью. Вы скажете, что игру можно останавливать. Ну может и так. Игрок зевнувший может даже сам сдаться в такой ситуации.

19.07.2022, 13:17 Усов Геннадий Григорьевич Отзыв: " Очевидно, это относится к разделу «Математика». Что здесь не так?" - Далеко не очевидно. Вы вводите в обращение другую математику - "Математику мужественности и женственности". Вот под этой математикой и оформляйте свою статью. "Если мужественность и женственность рассматривать исключительно в контексте силы, то мужественное это сильное, а женственное – слабое." - А это у Вас будут "математические операции".

19.07.2022, 13:20 Усов Геннадий Григорьевич Отзыв: Вы не рассматриваете важный элемент игры. (1) и (2) имеют по 99 очков. (1) берет ещё очки и становится слабым. (2) берет у него очки и становится слабым. А если он взял при том много очков, то (1) может стать сильным.

19.07.2022, 13:22 Усов Геннадий Григорьевич Отзыв: А про 999 совсем отдельная песня. Как добраться до 999, когда тебя все бьют, поскольку у них по 99.

19.07.2022, 13:25 Усов Геннадий Григорьевич Отзыв: Теперь по сокращению статьи. достаточно указать основные моменты, которые обсуждались в отзывах: 9 - 99 - 999, объдинение, 99 - 129 - 102 и т.д. А игроки об остальном сами дойдут. И достаточно 1 - 2 картинок.

19.07.2022, 15:51 Усов Геннадий Григорьевич Отзыв: " Напомню, что заполненность разрядов чисел в двоичной системе может быть использовано для описания мужественности и женственности. Если мужественность и женственность рассматривать исключительно в контексте силы, то мужественное это сильное, а женственное – слабое. Что здесь не так?" - По-моему, Вы начали путаться в определениях. Мужественность и женственность у Вас в двоичной системе. А в статье у Вас десятичная система. Где у Вас мужественность и женственность в десятичной системе ?

20.07.2022, 0:50 Харт Алекс Отзыв: «Вы не рассматриваете важный элемент игры. (1) и (2) имеют по 99 очков. (1) берет ещё очки и становится слабым. (2) берет у него очки и становится слабым. А если он взял при том много очков, то (1) может стать сильным.» - Вы сейчас пишете до конца не продумав. Представьте два короля (1) и (2) находятся рядом и имеют 99 очков. Вы пишете, что (1) берет очки и становится слабым. Здесь надо пояснение, потому что здесь много вариантов. Если (1) просто берет очки без какой-либо договоренности с кем-либо из королей, то это глупый ход, или во всяком случае рискованный. Конечно надо смотреть по ситуации, возможно где-то такой ход будет оправдан. Но в большинстве случаев этот ход будет глупым. Представьте (1) ослаб получив число 139. Это не такое слабое число, но по сравнению с 99 это слабо. Потом (2) совершенно спокойно может напасть на (1) и получить скажем те же 139 очков, но при этом король (2) может сделать так, чтобы у (1) при этом было очень слабое число, например 110, или 90. Т.е. после этого (1) не может стать очень сильным, как пишете Вы. В этом и есть грамотность хода, как и в шахматах, есть глупые ходы, есть умные. Когда король ходит, он должен смотреть не только на то, какое число получит он сам, но и какие числа станут у других королей. В Вашем примере королю (2) не стоит брать карты у (1) так, чтобы (1) стал снова сильным королем. Напротив, в этой ситуации (2) может ослабить (1) окончательно. Поэтому я и пишу, что ход (1) был глупым или рискованным. Учитывайте еще, что слабость слабости рознь. 139 не такое слабое число, а 90 очень слабое. Теперь другой вариант. Король (1) взял карты и ослаб, имея какую-то договоренность с другим королем о поддержке. Вот здесь уже этот ход может быть вполне нормальным. Так как союзный договор с другим королем это важный фактор.

20.07.2022, 0:50 Харт Алекс Отзыв: «Далеко не очевидно. Вы вводите в обращение другую математику - "Математику мужественности и женственности". Вот под этой математикой и оформляйте свою статью.» - Геннадий Григорьевич, кажется Вы опять начинаете чего-то не догонять. Введено математическое понятие не женственность и мужественность, а заполненность разрядов чисел. Написано про то, что это некоторое расширение понятия остатка от деления. Ну вот представьте, когда-то ввели понятие остатка от деления. И Вы скажете: «Вы вводите в обращение другую математику. Математику остатков от деления.». Для фактической заполненности есть определение, формула как она вычисляется. Посмотрите статью «Абсолютная и фактическая заполненность разрядов чисел», формулы (6) и (9). Это не математические формулы? Не математические величины? О какой другой математике Вы говорите? Или по Вашему любое новое понятие в математике это сразу другая математика? Поясните свой тезис. Что за другая математика. Почему это не новое понятие в текущей математике? «…то мужественное это сильное, а женственное – слабое." - А это у Вас будут "математические операции"» - Опять не догоняете. Мужественность и женственность это применение математического понятия заполненность разрядов чисел в двоичной системе счисления в философском осмыслении двойственности этого мира.

20.07.2022, 0:51 Харт Алекс Отзыв: «А про 999 совсем отдельная песня. Как добраться до 999, когда тебя все бьют, поскольку у них по 99.» - А как Вы хотели? Раз, раз и всех побелил? Пришел, увидел, победил? Если играет много королей, то понятно, что не все достигнут 99 очков. Многие проиграют в начале. Кто-то будет с кем-то договариваться. При союзе королей вполне реально достигать сильных чисел 199, 299, 399 и т.д. Кроме того будут и короли среди большого их количества, которые в одиночку достигли чисел 199, 299, 399 и т.д. Вам кажется это невозможным? Еще учтите, если король достиг числа 199 или 299, то он может в некоторых своих ходах сразу набирать 100 очков за ход (т.е. например с 299 на 399), так как его масштаб большой, много соседних карт, которые он потенциально может присоединить к своей территории. В начале игры, когда король совсем один он может присоединить максимум 4 карты. А когда империя короля велика, то он может присоединять уже много карт за один ход. Все зависит от масштаба империи короля.

20.07.2022, 0:52 Харт Алекс Отзыв: «Теперь по сокращению статьи. достаточно указать основные моменты, которые обсуждались в отзывах: 9 - 99 - 999, объдинение, 99 - 129 - 102 и т.д. А игроки об остальном сами дойдут. И достаточно 1 - 2 картинок.» - Ну вот согласитесь, на Вашем примере я понял, что возможно статью надо не сократить, а напротив увеличить, добавив еще один пример игры. На этот раз «в закрытую». Потому что при полном описании игры выяснилось, что Вы очень много не поняли. Как остальные читатели что-то поймут, если будет 1-2 картинки? Формально статья не нарушает правил. Количество знаков меньше 30000. Приводится для читателей пример партии в предлагаемую игру с полным описанием возможного сценария ее развития. Для понимания читателей это не плохо. Почему бы и не привести в таком случае такое полное описание игры. Кому от этого плохо? Если кому-то все понятно сразу. Ну хорошо. Он может и не читать полное описание. Но не всем все сразу понятно.

20.07.2022, 0:53 Харт Алекс Отзыв: «По-моему, Вы начали путаться в определениях. Мужественность и женственность у Вас в двоичной системе. А в статье у Вас десятичная система. Где у Вас мужественность и женственность в десятичной системе ?» - А я и пишу «Напомню, что заполненность разрядов чисел в двоичной системе может…». Я нигде не писал про мужественность и женственность в десятичной системе. В десятичной системе предлагается определять силу империи королей.

20.07.2022, 12:08 Усов Геннадий Григорьевич Отзыв: «…я понял, что возможно статью надо не сократить, а напротив увеличить,» - Дарю Вам идею как сократить статью. Примерная схема: Главное в начале игры: последняя цифра должна быть 9. И прибавлять надо числа, кратные 10. Если нет рядом другой «империи», то можно выстроить последовательность приобретений за несколько ходов (видя поле) таким образом, чтобы к моменту контакта с другой «империей» у Вас будет на конце цифра 9. При этом надо стараться увеличивать по сравнению с другой империей вторую цифру. Сложнее тем «империям», которые «стартуют» позже: как правило, у них всегда будет число менее сильное. Поэтому у тех, кто стартует раньше, есть возможность забрать что-то у тех, кто стартует позже и не набрал хорошую вторую цифру. …. И так далее. После этих слов (или похожих по смыслу с развитием темы) можно убрать из статьи половину картинок. С Дамами и Вальтами сложнее: там нужно сразу переходить на конечную цифру 9.

20.07.2022, 12:18 Усов Геннадий Григорьевич Отзыв: Из-за неверной оценки поля (в предыдущем отзыве) у короля червей первый ход ошибочный: сначала надо было брать всё, получалось 33, а затем взять 4,5,7 и получится 49 вместо Ваших 39.

20.07.2022, 12:21 Усов Геннадий Григорьевич Отзыв: Далее с ходу можно "бить" сначала короля крестей, а затем, пока не успел сформироваться король бубей, "бить" его. Защищайтесь. Вот что значит иметь ПЕРВЫЙ ход!

20.07.2022, 12:24 Усов Геннадий Григорьевич Отзыв: Вместо картинок, если хотите отследить путь, можно создать "строку империи": Кк, 7к, Тб, и т.д. Пр этом иметь только начальную картинку.

21.07.2022, 17:44 Харт Алекс Отзыв: «Дарю Вам идею как сократить статью. Примерная схема:» - Данная схема несколько неточная. Довольно грубое приближение. «Главное в начале игры: последняя цифра должна быть 9.» - Не всегда это возможно, тогда 8, если не 8, то 7. Должен быть баланс, что-то среднее между максимальным расширением, но ослаблением и небольшим расширением, но с сохранением сильного числа. Например будет вариант расширения с 19, до 29 или 48. Конечно надо смотреть по конкретным обстоятельствам, но вариант расширения до 48 возможно будет более правильным. «И прибавлять надо числа, кратные 10.» - Если у Вас в конце 9 и есть возможность значительного расширения с сохранением в конце 9, то да. Сумма присоединенных чисел будет кратна 10. Но исходя из вышесказанного, не всегда у Вас будет 9. Если у Вас 8, то желательно будет присоединить число, которое делится на 10 с остатком 1. «Если нет рядом другой «империи», то можно выстроить последовательность приобретений за несколько ходов (видя поле) таким образом, чтобы к моменту контакта с другой «империей» у Вас будет на конце цифра 9.» - Условие иметь цифру 9 на момент контакта с другой империей не является ни необходимым, ни достаточным. Если у другой империи, с которой будет контакт, цифра 8, то и Вам достаточно иметь не ниже 8 в конце. С другой стороны, если у соседней империи число 79, а Вы будете рядом с ней имея число 59. То число 9 в конце Вам не поможет. Правило скорее такое: нужно на момент контакта с другой империей иметь число более сильное, чем у нее. Это общее правило. В разных ситуациях все по-разному. «При этом надо стараться увеличивать по сравнению с другой империей вторую цифру.» - В целом Ваше число должно быть сильнее, чем у соседней империи. Верно, что сперва влияет 1-я цифра, затем 2-я и т.д. Если же достигнуто число 99, то дальнейшее расширение приведет к неизбежному ослаблению (пока не достигнуто более сильное число 199). Здесь уже дилемма. С одной стороны надо расширяться, а с другой надо не ослабляться. На этом этапе многое будет определяться договорами с другими королями. «Сложнее тем «империям», которые «стартуют» позже: как правило, у них всегда будет число менее сильное. Поэтому у тех, кто стартует раньше, есть возможность забрать что-то у тех, кто стартует позже и не набрал хорошую вторую цифру. ….» - Я уже писал про то, что очередность хода это не единственный фактор влияющий на победу. «И так далее. После этих слов (или похожих по смыслу с развитием темы) можно убрать из статьи половину картинок.» - Пока не уверен в этом. Вообще вопрос сокращения статьи это последний вопрос. Сейчас у Вас понимания стало несколько больше, чем ранее. Но всё же к вопросу сокращения статьи нужно возвращаться, когда у Вас будет полное понимание игры. Когда всё понятно, и правила, и описываемая партия, почему тот или иной король пошел именно так, что это вполне логично, вот тогда можно поговорить о сокращении статьи. «С Дамами и Вальтами сложнее: там нужно сразу переходить на конечную цифру 9.» - А в чем тут сложнее? Игра «Дамы» по-сути идентична игре «Короли». Только в первой дама – 19, а король – 15. Т.е. дама и король меняются местами. Почему так? Если этого не сделать, т.е. дама это 15 очков, то на первом ходе она не сможет взять такие карты как 6, 7, 8, 9, 19. Может оказаться так, что она совсем ничего взять не сможет. Число 19 не случайно приписано королю в игре «Короли» и даме в игре «Дамы». Чтобы соответственно и король и дама по силе были самыми сильными картами в игре. В предлагаемой вами вариации «Вальты» полагаю, что валет будет 19 очков. Иначе если ему оставить 11 очков он сможет взять только туза (1 очко), 10 и джокера (0 или 50 очков).

21.07.2022, 17:44 Харт Алекс Отзыв: «Вместо картинок, если хотите отследить путь, можно создать "строку империи": Кк, 7к, Тб, и т.д. Пр этом иметь только начальную картинку.» - Думаете это будет наглядно? Например, в шахматах имеется начальное расположение фигур, а оно всегда одинаковое, и далее строка кто куда пошел. И думай, гадай как же расположены фигуры на текущий момент. Вычисляй это в голове исходя из строки ходов. В общем не очень понял Ваше предложение.

21.07.2022, 17:45 Харт Алекс Отзыв: «Из-за неверной оценки поля (в предыдущем отзыве) у короля червей первый ход ошибочный: сначала надо было брать всё, получалось 33, а затем взять 4,5,7 и получится 49 вместо Ваших 39.» - Геннадий Григорьевич, торопитесь. Если у короля червей будет число 33, то он не сможет потом присоединить 4, 5 и 7, так как эти независимые государства сильнее, чем он. По-моему в статье явно не написано (лень сейчас искать), но есть такой текст в правилах: «Напасть может только более сильный король на более слабого.». Тут речь про королей. Но короли это те государства, за которых играют игроки, и то не всегда. Могут играть 3 игрока в игру, и тогда четвертый король будет просто как карта, за которую никто не играет. Но эта карта остается государством (город-государство), просто его никто не развивает. Т.е. смысл в том, любая карта на столе, которую не присоединили к другой империи, это независимое государство. Неважно играет за нее кто-то или нет. Это государство. И напасть можно только на более слабое государство. Государство с числом 33 не может напасть на государства с числами 4, 5 и 7. «Далее с ходу можно "бить" сначала короля крестей, а затем, пока не успел сформироваться король бубей, "бить" его. Защищайтесь.» - Как Вы уже поняли, не получится так бить других королей. «Вот что значит иметь ПЕРВЫЙ ход!» - Вы несколько преувеличиваете первый ход. И преуменьшаете фактор расположения короля. Король червей находится с краю.

22.07.2022, 7:25 Усов Геннадий Григорьевич Отзыв: "Если у короля червей будет число 33, то он не сможет потом присоединить 4, 5 и 7, так как эти независимые государства сильнее, чем он. " - Вы нигде не говорите, что любая карта - это как минимум княжество, и которое надо присоединять по правилам сильного.

22.07.2022, 11:21 Усов Геннадий Григорьевич Отзыв: После обсуждения настоящей статьи в отзывах я ещё больше склоняюсь к тем замечаниям, которые мной были высказаны в рецензии: 1. Статья перегружена, её нужно и можно значительно сократить. 2. Из статьи нужно убрать раздел "математика", поскольку в этой статье имеет место специальная система подсчёта очков. Если в статье появляются числа, то это не означает, что эту статью нужно рассматривать в разделе "математика".

22.07.2022, 23:35 Харт Алекс Отзыв: «Вы нигде не говорите, что любая карта - это как минимум княжество, и которое надо присоединять по правилам сильного.» - То, что княжество, говорю в правиле 8: «Т.е. однозначные числа – это княжество, двузначные – королевство, трехзначные – империя.». Думал, что правило сильного очевидно распространяется на любое государство, не важно играет за него кто-то или это отдельная карта. Для большей ясности в правиле 7 дал дополнительное пояснение: «Данное правило распространяется и на присоединение к империи короля отдельных карт (не включенных ни в какую империю). Например, империя короля с итоговым числом 33 не может присоединить к себе такие отдельные карты: 4, 5, 6, 7, 8, 9, дама (15), король (19).»

22.07.2022, 23:36 Харт Алекс Отзыв: «После обсуждения настоящей статьи в отзывах я ещё больше склоняюсь к тем замечаниям, которые мной были высказаны в рецензии: 1. Статья перегружена, её нужно и можно значительно сократить.» - Во-первых, Вы не поверите, статья уже сокращена. В первоначальной версии статьи было приведено два примера игры с их полным описанием. Беда в том, что размер статьи превысил допустимый лимит. Пришлось оставить описание только одной партии игры. Если была бы статья с описанием двух примеров, то думаю и у Вас, и у других читателей понимание правил игры могло бы прийти проще. Во-вторых. Больше это не меньше. Кто понимает всё сразу, может не читать то, что для него очевидно. Но не все такие умные. Им действительно нужен текст с полным описанием примера сыгранной партии. В-третьих. Вы ратуете за сокращение статьи. Какую цель Вы преследуете? Вам не хочется утруждать излишним чтением тех, кто будет ее смотреть? Какие здесь проблемы? Например, мне надо посмотреть что-то в Википедии. Например, прочитать про население в городе Краснодар. Я открываю статью. Но в ней про всё. И про климат, и про историю города. Что мешает мне пропустить неинтересный мне текст и читать только то, что мне нужно? Еще раз. Больше это не меньше. В-четвертых. Лимит статьи не превышен. Не вижу совсем никаких проблем с «перегрузкой». Наоборот, считаю, что подробное описание полезно. Даже необходимо. «2. Из статьи нужно убрать раздел "математика", поскольку в этой статье имеет место специальная система подсчёта очков.» - Специальная это какая? И какие еще бывают? Приведите примеры. «Если в статье появляются числа, то это не означает, что эту статью нужно рассматривать в разделе "математика".» - Если просто числа, то не нужно. Согласен. А если впервые. Подчеркиваю впервые. Предлагается игра, в которой используется новое. Подчеркиваю новое. Математическое понятие заполненности разрядов, то эту игру просто обязательно нужно добавить в раздел «Математика». Статья, в которой вводится это понятие, опубликована в разделе «Математика». А вот о применении этого понятия статей нет. Это и есть статья о применении данного математического понятия в игре. Поэтому статью «Математическая игра «Империи»» грех не публиковать в разделе «Математика». Как иначе? Кстати соответствующий УДК указан.

25.07.2022, 14:28 Усов Геннадий Григорьевич Отзыв: Автор статьи и рецензент остаются при своём мнении. Поэтому продолжение дискуссии вида "белое - чёрное" при настоящем виде статьи не представляется возможным.

27.07.2022, 11:14 Харт Алекс Отзыв: Автор статьи показал рецензенту всё его недопонимание. При этом рецензент остался при своем мнении. "Кстати, а почему только прямоугольник, а не произвольный "ступенчатый" плоский объект? И почему числа только до 10, а не до 35, 109, 287 и т.д.?" - Что это было? Рецензент не убрал из рецензии даже это замечание, говорящее о его тотальном недопонимании. Автор же статьи одну правку в статье сделал, согласившись, что без нее одно из правил игры может быть не понятно читателям. Но автор статьи не видит обновленной рецензии, которая по мнению автора должна последовать после раскрытия тотального недопонимания у рецензента. Парадокс в том, что рецензент настаивает на тотальном сокращении статьи, тогда как именно он и не понял игру при полном ее описании. Сокращение статьи не может являться главным замечанием. Что же является главным замечанием рецензент не уточняет. Он раскритиковал игру не поняв её. Но даже когда ему всё объяснили не видно рецензии, в которой написано, что к самой игре, к ее правилам, вопросов нет.

27.07.2022, 12:17 Усов Геннадий Григорьевич Отзыв: Автор статьи остановился только на одном серьёзном замечании: сокращение статьи. Но есть ещё серьёзное замечание: в статье нет МАТЕМАТИКИ, а есть механизм определения очков: большее число признаётся меньшим по некоторому определению.

27.07.2022, 13:02 Усов Геннадий Григорьевич Отзыв: Кстати, есть в настоящем журнале раздел "Физика". В статьях данного раздела очень много своих, физических формул, где есть степени, синусы, корни и т. д. Но в этих статьях нет дополнительного раздела "Математика". Каждому своё.

29.07.2022, 1:38 Харт Алекс Отзыв: «Кстати, есть в настоящем журнале раздел "Физика". В статьях данного раздела очень много своих, физических формул, где есть степени, синусы, корни и т. д. Но в этих статьях нет дополнительного раздела "Математика". Каждому своё.» - Если в физике применяются уже известные математические формулы, операции и т.д., тогда статья к математике не имеет отношения. Если же впервые показывается применение (и цель статьи именно показать это применение) какого-то нового математического понятия, то статья может быть отнесена к математике. Рецензенту нужно не искать какие-то зацепки, чтобы оправдать свою первоначальную рецензию, с которой он явно перестарался, а напротив искать малейшие зацепки, чтобы дать другую рецензию, для того чтобы способствовать продвижению этой очень интересной математической игры. В игре «Короли» одна партия интереснее другой, а рецензент ее «динамит». Где логика?

29.07.2022, 1:38 Харт Алекс Отзыв: «Автор статьи остановился только на одном серьёзном замечании: сокращение статьи.» - Это не должно быть серьезным замечанием. Рецензент не ответил зачем ему нужно сокращение статьи. Он не хочет утруждать излишним чтением людей? Он бережет бумагу в том случае если кто-то захочет распечатать данную статью на принтере? Или он не хочет утруждать специалиста, который будет приводить внешний вид статьи к нужному в том случае если статью опубликуют в данном журнале? «Но есть ещё серьёзное замечание: в статье нет МАТЕМАТИКИ» - Есть применение нового математического понятия. Показать это применение более чем актуально. УДК 51-8, Математические игры и развлечения. «а есть механизм определения очков: большее число признаётся меньшим по некоторому определению.» - Хороший пример, ясно показывающий, что рецензент снова «не догоняет». Много раз уже повторял, что заполненость разрядов это некоторое расширение понятия остатка от деления. Возьмем два числа: 111 и 17. Первое больше второго. Но остаток от деления на 10 больше у второго числа. И рецензент делает вывод: «большее число признаётся меньшим». С чего бы? Рецензент путает само число, его величину, и значение какого-то его свойства. А виноват конечно автор.

30.07.2022, 8:54 Усов Геннадий Григорьевич Отзыв: "Рецензенту нужно не искать какие-то зацепки, чтобы оправдать свою первоначальную рецензию, с которой он явно перестарался, а напротив искать малейшие зацепки, чтобы дать другую рецензию, для того чтобы способствовать продвижению этой очень интересной математической игры." - Рецензент не мешает продвижению игры. И это было показано как в отзывах, так и в рецезии. Были даны рекомендации. Переводите игру в раздел "Спорт", и пусть рецензенты по спорту решают судьбу Вашей игры. А поскольку статья пока находится в разделе "Математика", то моё мнение: её надо сократить.

30.07.2022, 9:07 Усов Геннадий Григорьевич Отзыв: "Есть применение нового математического понятия." Вот и объясните это НОВОЕ понятие. Лучше в отдельной статье, так как это уже фундаментальный труд. При этом сошлётесь на статью по спорту. А одной фразы - "Возьмем два числа: 111 и 17. Первое больше второго. Но остаток от деления на 10 больше у второго числа. " - явно недостаточно для фундаментального труда.

1.08.2022, 0:07 Харт Алекс Отзыв: "Вот и объясните это НОВОЕ понятие. Лучше в отдельной статье, так как это уже фундаментальный труд." - Я же уже Вам писал про эту отдельную статью: https://sci-article.ru/stat.php?i=1635199247. На неё есть ссылка в текущей статье. "А одной фразы - "Возьмем два числа: 111 и 17. Первое больше второго. Но остаток от деления на 10 больше у второго числа. " - явно недостаточно для фундаментального труда." - Естественно. Поэтому и была написана приведённая выше фундаментальная статья. А эта статья о применении нового математического понятия в игре.

1.08.2022, 0:11 Харт Алекс Отзыв: "Рецензент не мешает продвижению игры. И это было показано как в отзывах, так и в рецезии." - Да, по рецензии это очень чётко видно. "А поскольку статья пока находится в разделе "Математика", то моё мнение: её надо сократить." - Это Ваше главное замечание на текущий момент?

1.08.2022, 9:48 Усов Геннадий Григорьевич Отзыв: "Поэтому и была написана приведённая выше фундаментальная статья. А эта статья о применении нового математического понятия в игре." - Вы называете статью [2] фундаментальным трудом??? Я полностью согласен с первым отзывом по статье [2]! А по поводу фундаментальности... Определение преимущества числа А над числом В по их mod 10, mod 100, mod 1000, и т.д. Это Вы считаете фундаментальностью? Не смешите меня.

1.08.2022, 9:52 Усов Геннадий Григорьевич Отзыв: "Это Ваше главное замечание на текущий момент?" - Главное замечание - в статье нет такой математики, с помощью которой статья может претендовать на включение в раздел МАТЕМАТИКА!

2.08.2022, 0:31 Харт Алекс Отзыв: «Главное замечание - в статье нет такой математики, с помощью которой статья может претендовать на включение в раздел МАТЕМАТИКА» - Статья о применении нового математического понятия заполненности разрядов, которое дано в статье [2]. Данная статья не фундаментальна (фундаментальна статья [2]). С этим никто не спорит. Но все-таки статья о применении нового математического понятия. Это математика.

2.08.2022, 0:31 Харт Алекс Отзыв: «Вы называете статью [2] фундаментальным трудом???» - Естественно считаю. «Я полностью согласен с первым отзывом по статье [2]!» - А я согласен со вторым отзывом. «А по поводу фундаментальности... Определение преимущества числа А над числом В по их mod 10, mod 100, mod 1000, и т.д. Это Вы считаете фундаментальностью?» - Вы сами понимаете, что Вы в очередной раз не догоняете? Практически в каждом Вашем ответе есть что-то, что говорит о том, что Вы не догоняете. Ужас. Во-первых, мы говорили о фундаментальности статьи [2]. Где в ней написано про определение преимущества одного числа перед другим? Во-вторых, Вы так и не догнали определение заполненности разрядов. В данной статье есть фраза «Как показано в работе [2], фактическая заполненность разрядов представляет собой перевернутую запись числа в соответствующей системе счисления.». Подчеркиваю: «перевернутую запись числа». Т.е. наибольшим приоритетом будет обладать последняя цифра числа (разряд единиц), затем предпоследняя и т.д. Пример, два числа 1279 и 1674. Возьмем mod 1000, как Вы пишете. Получим 279 и 674. У второго числа больше. По Вашей логике это число должно быть сильнее. Тогда как если взять перевернутые записи, то мы получим 9721 и 4761. У первого больше. Т.е. первое число должно быть сильнее. Вы не догоняете, что в Ваших mod приоритет порядков остается такой же, как в самом первоначальном числе, только оно несколько обрезано. А нужен обратный порядок. В-третьих, а что если по условиям игры будет не просто определяться какое число сильнее, а чуть сложнее. Например, напасть одна империя на другую может только в том случае, если процент заполненности разрядов у первой империи больше чем у второй империи как минимум на 5%. Как Вы будете через mod это записывать? В-четвертых. Определение заполненности разрядов дано в фундаментальном труде [2]. Оно может казаться Вам бессмысленным, но это определение и точка. Точно так же есть понятие совершенных чисел. Я тоже могу написать, что оно бессмысленно. Берут сумму делителей. И если сумма всех делителей в 2 раза больше самого числа, то число валяется совершенным. А если в три раза, то нет. В четыре – нет. Только в 2 раза. Бред. С чего данное число является вдруг совершенным? И самое главное, где это можно реально применить? В физике? В химии? В астрономии? Где? Нигде. А понятие дружественных чисел не бессмысленно? Вы не догоняете. Это определение и точка. А смысл можно видеть в нем, можно не видеть. Это другой вопрос. Точно также и определение заполненности разрядов. Это определение и точка. И в фундаментальном труде [2] оно даётся. С чего вдруг статья [2] дающая новые определения не является фундаментальным трудом? Потому что Вы не увидели смысла в новых понятиях? Понятия, тем не менее, даны. А эта статья о применении нового понятия в игре. «Не смешите меня.» - По уровню того, сколько Вы не догоняете, Вам, по всей видимости, должно быть не до смеха.

2.08.2022, 14:40 Усов Геннадий Григорьевич Отзыв: Вы хотите меня переубедить количеством слов? Информации в ответе хватает на изложение её в нужном виде на 4-5 строчках. - " Пример, два числа 1279 и 1674. Возьмем mod 1000, как Вы пишете. Получим 279 и 674. У второго числа больше. По Вашей логике это число должно быть сильнее. Тогда как если взять перевернутые записи, то мы получим 9721 и 4761." - Заметили, что я перечислял mod? Так сначала сравнение по mod 10, потом по mod 100, потом по mod 1000, и т.д. По mod 10 число 1279 сильнее, чем число 1674. А если числа одинаковы по mod 10, смотрим по mod 100. И т.д.

3.08.2022, 0:22 Харт Алекс Отзыв: «Информации в ответе хватает на изложение её в нужном виде на 4-5 строчках.» - Для Вас не хватит. Чтобы Вы поняли нужно расписать всё очень и очень подробно. Да Вы и ответили из всех моих аргументов только на один. «Заметили, что я перечислял mod? Так сначала сравнение по mod 10, потом по mod 100, потом по mod 1000, и т.д. По mod 10 число 1279 сильнее, чем число 1674. А если числа одинаковы по mod 10, смотрим по mod 100. И т.д.» - Да. Я это заметил. Т.е. если Вы были бы программистом, и у Вас была бы задача реализовать эту игру на компьютере, то Вы именно так бы проверяли какая империя сильнее? В цикле прогоняли бы остатки от деления начиная с 10 и далее? А потом руководство сказало бы Вам, что нужно немного изменить правила игры согласно моему «в-третьих» из предыдущего отзыва, то как бы Вы стали переделывать свой алгоритм? Не проще было бы изначально ориентироваться именно на заполненность разрядов, обратную запись числа, раз в статье четко сказано, что сила империи это заполненность разрядов?

3.08.2022, 7:54 Усов Геннадий Григорьевич Отзыв: "Не проще было бы изначально ориентироваться именно на заполненность разрядов, обратную запись числа, раз в статье четко сказано, что сила империи это заполненность разрядов?" А чем это отличается от прибавления к числу другого числа, когда эти разряды у первого числа заполняются?

3.08.2022, 10:43 Харт Алекс Отзыв: "А чем это отличается от прибавления к числу другого числа, когда эти разряды у первого числа заполняются?" - Не понял вопроса. Можете пояснить на конкретном примере?

3.08.2022, 14:28 Усов Геннадий Григорьевич Отзыв: Зачем говорить о заполнении разрядов, когда можно сказать проще - идёт сложение чисел.

3.08.2022, 15:11 Харт Алекс Отзыв: А если идет умножение чисел, то как правильно говорить о заполненности разрядов?

3.08.2022, 15:42 Усов Геннадий Григорьевич Отзыв: А у Вас в статье только сложение. Поэтому можете спокойно упростить статью, говоря о mod.

3.08.2022, 16:38 Харт Алекс Отзыв: Т.е. я в статье должен написать: "Какая империя сильнее определяется в цикле. Сначала mod 10, mod 100 и т.д."? И Вы полагаете, что какой-то смысл есть в Ваших mod в цикле? По mod в цикле Вы можете определить какая империя сильнее. (Смысла в этом нет, но определить можно.) Ну а чему равна сила империи? Кроме того моё "в-третьих" Вы игнорируете? Вы принципиально хотите игнорировать понятие заполненности разрядов пытаясь заменить его на mod? Для двузначного числа Вы так можете записать фактическую заполненность через mod: "Фактическая заполненность двузначного числа A = 10 * mod 10 (A) + (mod 100 (A) – mod 10 (A)) / 10". Я правильно Вас понял, Вы считаете, что раз фактическую заполненность можно вычислить через несколько mod отсюда вытекает что понятие, заполненность разрядов не нужно?

3.08.2022, 17:53 Усов Геннадий Григорьевич Отзыв: "Я правильно Вас понял, Вы считаете, что раз фактическую заполненность можно вычислить через несколько mod отсюда вытекает что понятие, заполненность разрядов не нужно?" - Вы правильно меня поняли. Вы придумали игру. Это интересная игра. Есть способ определения очков. Оригинальный, не спорю. Что-то в этом есть. Хотя при игре на большее количестве карт после 100 может быть бесконечный случай. Так мне кажется. Но зачем в эту игру ещё "тянуть" какую-то теорию по разрядности? Что-бы на основании игры что-то кому-то доказать?

3.08.2022, 23:10 Харт Алекс Отзыв: «Вы правильно меня поняли.» - Я правильно Вас понимаю, что вводить понятия синуса и косинуса не нужно, поскольку они выражаются через экспоненту по формулам Эйлера? «Что-то в этом есть.» - Именно этими же словами – «Что-то в этом есть» - об этой игре говорили не только Вы. «Хотя при игре на большее количестве карт после 100 может быть бесконечный случай. Так мне кажется.» - Опишите его пожалуйста. «Но зачем в эту игру ещё "тянуть" какую-то теорию по разрядности?» - Потому что без этой теории не понятен смысл обратной записи числа. Почему вдруг силу империи можно сопоставить с обратным значением числа. А данная теория это объясняет, так же как она объясняет и применение заполненности разрядов для описания мужественности / женственности. «Что-бы на основании игры что-то кому-то доказать?» - Игра показывает применение понятия заполненности разрядов. Какие-то объекты сопоставляются с числами (в игре это империи, или территории королей). Свойства этих объектов это системы счисления (в игре рассматривается только одно свойство, это сила – 10-ная система счисления). А значение заполненности разрядов в этой системе счисления определяет значение этого свойства у конкретного объекта. То же самое было с мужественностью / женственностью. Только там свойство было «мужественность / женственность» - 2-ная система счисления.

4.08.2022, 7:52 Усов Геннадий Григорьевич Отзыв: (1)Приехали! - "Игра показывает применение понятия заполненности разрядов." - Так что главное в статье: игра или разряды? (2) "Потому что без этой теории (разрядности) не понятен смысл обратной записи числа." - Очень даже понятен смысл обратной записи числа. Вам нужна обратная запись для того, чтобы сравнивать младшие разряды. А для этого очень удобен mod - математическая операция. Вы же ратуете за математику!

4.08.2022, 11:31 Харт Алекс Отзыв: «Так что главное в статье: игра или разряды?» - Мне одинаково важно: дать саму игру, и показать применение в ней заполненности разрядов. Это важный момент, который Вы хотите убрать: что сила империи может быть сопоставлена с заполненностью разрядов. «Очень даже понятен смысл обратной записи числа. Вам нужна обратная запись для того, чтобы сравнивать младшие разряды.» - Нужно теоретическое обоснование этого: почему младшие разряды вдруг стали иметь больший вес, чем старшие разряды. «А для этого очень удобен mod - математическая операция.» - Вы упускаете из виду главное. Для сравнения (причем не только больше/меньше, но и на сколько больше/меньше) нужна величина заполненности разрядов. Именно ее мы сравниваем. Данная величина имеет отношение к конкретной системе счисления, на сколько заполнены разряды числа в той или иной системе счисления. Величину каждого разряда с помощью mod (или комбинации из нескольких mod) вычислить можно, да и сам перевод числа в другую систему счисления можно выполнить с помощью mod. Т.е. mod это просто инструмент, а весь смысл именно в понятии заполненности разрядов. Представьте, что Вы с помощью молотка можете сделать себе стол. А я Вас спрошу: зачем Вам стол, когда у Вас есть молоток?

4.08.2022, 17:08 Усов Геннадий Григорьевич Отзыв: Рассмотрим Ваш пример (из статьи) - "Ход короля бубен. Максимально можно взять четыре карты достоинством: 1, 3, 9, 11. Итоговое число станет равно 43. Это слабое число. Поэтому имеет смысл не брать туза крестей и 3 бубен. Итоговое число будет равно 39." - 43 слабое по сравнению с 39, потому что 3 меньше 9. То есть, здесь "сработал" mod 10. На основании его число 43 признаётся слабым. И этого достаточно.

4.08.2022, 17:50 Харт Алекс Отзыв: А если сравнивать 49 и 39? Уже одним mod не обойтись. Нужен Ваш цикл. Кроме того, нужно пояснение. Что мы делаем. А мы делаем опять же сравнение обратных записей. А если сравнивать 9 и 7? Даже mod не нужен. Достаточно сравнить саму величину чисел. Это всё частные случаи. А общий случай, это обратная запись числа.

4.08.2022, 19:01 Усов Геннадий Григорьевич Отзыв: Великолепно! Вы сами сейчас нашли более лучшее определение операций в игре: "А мы делаем опять же сравнение обратных записей. .... А общий случай, это обратная запись числа." - Пишите в статье - обратная запись и убирайте всю Вашу теорию про разряды.

5.08.2022, 0:41 Харт Алекс Отзыв: «Пишите в статье - обратная запись и убирайте всю Вашу теорию про разряды.» - Простите, а если бы в игре использовалось понятие не фактическая (формула (6) статьи [2]), а абсолютная (формула (11) статьи [2]) заполненость, то как правильно я должен был написать в данной статье?

5.08.2022, 8:56 Усов Геннадий Григорьевич Отзыв: Если бы да кабы ... Если в статье будет другое условие, то будем рассматривать новое условие.

5.08.2022, 12:35 Харт Алекс Отзыв: Вам не кажется, что нужно называть вещи своими именами? Если написать в статье "сравнение обратных записей", то собственно на ход самой игры это не повлияет. (Так же как не повлияет на расчет длины окружности, если Вы будете вычислять ее по формуле: Длина = 6.28 * r, нигде не упоминая число пи.) Но такой подход во-первых лишит теоретического обоснования почему мы можем силу империи рассчитывать именно так, во-вторых лишит статью одной из целей: как раз и показать применение нового математического понятия в игре.

5.08.2022, 13:35 Усов Геннадий Григорьевич Отзыв: В нашей дискуссии пошли повторения. Повторяю: в настоящей статье нет нового математического понятия, а есть способ определения: какое число больше (по Вашему - сильнее(?)). Как мы выяснили по предыдущим отзывам, этот способ похож на два других способа: по последовательному mod и по перевороту чисел (с добавлением нулей, если длина чисел разная). Поэтому повторно вести дискуссию и повторять предыдущие отзывы не хочется. Свою резензию на статью не меняю.

5.08.2022, 16:00 Харт Алекс Отзыв: "в настоящей статье нет нового математического понятия" - А где я говорил, что оно есть в настоящей статье? Оно есть в статье [2]. Почитайте раздел "Актуальность". "а есть способ определения: какое число больше" - Давайте ещё не будем вводить понятие "масса", а будем лишь говорить о способе узнать кто тяжелее. "этот способ похож на два других способа" - Способов рассчитать какую либо величину может быть много. И заполненность разрядов можно посчитать разными способами, и массу измерить можно разными способами. Но это не умаляет ни понятие заполненности разрядов, ни массу.

5.08.2022, 16:47 Усов Геннадий Григорьевич Отзыв: ""в настоящей статье нет нового математического понятия" - А где я говорил, что оно есть в настоящей статье? Оно есть в статье [2]. " - Тем более, если в статье нет ничего нового по математике, зачем эту статью включать в раздел МАТЕМАТИКА?

5.08.2022, 17:58 Харт Алекс Отзыв: Эта статья о применении нового математического понятия. И применение не где-то, а в математической игре - УДК 51-8 - это математика.

5.08.2022, 19:02 Усов Геннадий Григорьевич Отзыв: Применили - хорошо. Вот физики применяют формулы, а при этом не пишут, что статьи относятся к математике. Повторяю: в статье, которая относится к разделу "математика", должна быть новизна по математике, а она у Вас в статье [2]. В настоящей статье, как Вы сказали, есть только применение, что расходится с Вашим утверждением о математической новизне в разделе статьи "Научная новизна". А то, что Вы написали УДК 51-8 ещё не значит, что статья относится к этому разделу: написать можно любые разделы...

6.08.2022, 0:50 Харт Алекс Отзыв: "Применили - хорошо. Вот физики применяют формулы, а при этом не пишут, что статьи относятся к математике." - Если физики применили формулу, то они не пишут, что статьи относятся к математике. Верно. Но если математики нашли применение своей НОВОЙ формулы в физике, то вполне могут отнести статью к математике. Особенно если им важно показать применение своей новой формулы. "Повторяю: в статье, которая относится к разделу "математика", должна быть новизна по математике, а она у Вас в статье [2]." - Применение нового математического понятия - относится к математике. Применение в новой математической игре - относится к математике. Применение нового математического понятия - имеет математическую новизну. Применение в новой математической игре - имеет математическую новизну. "В настоящей статье, как Вы сказали, есть только применение, что расходится с Вашим утверждением о математической новизне в разделе статьи "Научная новизна"." - Есть применение НОВОГО понятия. И предложена НОВАЯ МАТЕМАТИЧЕСКАЯ игра. В чем расхождение? "А то, что Вы написали УДК 51-8 ещё не значит, что статья относится к этому разделу: написать можно любые разделы..." - И почему не относится? А теперь главное. Я в самом начале в первом отзыве написал, что у Вас есть один единственный слабый козырь, и Вы сейчас начинаете им пользоваться, за неимением других аргументов. Вам следует самому подтвердить и оправдать отнесение этой статьи к математике вместо того, чтобы показывать свой слабый козырь и спрашивать «а где математическая новизна», «а где научная новизна». Всё это при желании найти можно. А при нежелании конечно можно упереться и утверждать, что всего этого нет.

6.08.2022, 0:58 Харт Алекс Отзыв: "Создание интерактивной математической игры в среде Scratch для начальной школы" - Эту статью не подскажете почему опубликовали в разделе "Математика"? Что там нового сделано именно по математике исходя из Вашей логики?

6.08.2022, 7:52 Усов Геннадий Григорьевич Отзыв: "Создание интерактивной математической игры в среде Scratch для начальной школы" - Эту статью не подскажете почему опубликовали в разделе "Математика"? Что там нового сделано именно по математике исходя из Вашей логики?" - Чувствуется обида: этим можно, а мне нельзя. Отвечаю на вопрос: не знаю. Упомянутая статья должна быть по разделам педагогики и информационных технологий. И так иногда бывает.

6.08.2022, 8:28 Усов Геннадий Григорьевич Отзыв: "Применение нового математического понятия" - Я Вам в 3-ий раз говорю, что нет в статье нового математического понятия. Просто существующие способы по mod были "переназваны" в виде "некой силы" - сильное число. И дальше появилась некая теория на несколько страниц в обоснование этой СИЛЫ. Когда можно спокойно сказать: число больше по mod (...). И нет здесь ничего нового по МАТЕМАТИКЕ.

10.08.2022, 8:59 Усов Геннадий Григорьевич Отзыв: Вы не пояснили одну ситуацию. Если карты - княжества, то королевства берут эти княжества по "силе". Но не может королевство брать все княжества одновременно: так устроено королевство. Нельзя воевать на несколько фронтов. Поэтому княжества берутся друг за другом. И тогда перед оформлением очередного княжества "сила" королевства меняется. И тогда ...

13.08.2022, 22:48 Усов Геннадий Григорьевич Отзыв: Мне уже не нравится эта игра! Получается, что не обязательно в середине игры объединяться. Можно объединится трем игрокам в начале игры и "раздеть" четвертого игрока. При данной схеме подсчёта очков у четвертого игрока нет шансов на выигрыш при таком объединении! Кажется, что где-то Вы писали, что данная игра похожа на игру "Монополия". Совсем не похожа! В "Монополии", как мне помнится, остаются, как правило, два игрока, которые между собой соревнуются. И там честная игра друг против друга, а не игра одного против трех.

13.08.2022, 22:51 Усов Геннадий Григорьевич Отзыв: Допустим, на 52 картах идёт "игра" (если это называется игрой) одного против трех. А скольким игрокам надо объединиться, чтобы выиграть на 104 картах, на 108 картах, и т. д.? Сказали А, говорите Б.

16.08.2022, 1:28 Харт Алекс Отзыв: Вы кажется не ответили: "А то, что Вы написали УДК 51-8 ещё не значит, что статья относится к этому разделу: написать можно любые разделы..." - И почему не относится?

16.08.2022, 1:31 Харт Алекс Отзыв: «Чувствуется обида: этим можно, а мне нельзя.» - Ну что Вы. Какая обида. Просто не понятно где были Вы. Где Ваша рецензия на эту статью? «Отвечаю на вопрос: не знаю. Упомянутая статья должна быть по разделам педагогики и информационных технологий. И так иногда бывает.» - Да, только ни один из трех рецензентов такого замечания не сделал. В моей статье первый уважаемый рецензент такого замечания не сделал. Может быть четыре рецензента правы, а Вы нет? Впрочем, чего это я. Вы не можете быть не правы. Вы же доказали бинарную проблему Гольдбаха, и еще так, мимоходом, в своей последней статье доказали еще одну простую для Вас теорему по имени Ферма.

16.08.2022, 1:34 Харт Алекс Отзыв: «Я Вам в 3-ий раз говорю, что нет в статье нового математического понятия. Просто существующие способы по mod были "переназваны" в виде "некой силы" - сильное число. И дальше появилась некая теория на несколько страниц в обоснование этой СИЛЫ. Когда можно спокойно сказать: число больше по mod (...). И нет здесь ничего нового по МАТЕМАТИКЕ.» - У Вас в голове все окончательно спуталось. У Вас яйцо откладывает курицу, и из курицы вылупляется яйцо. «И дальше появилась некая теория на несколько страниц в обоснование этой СИЛЫ.» - Где на несколько страниц появляется эта теория? Фундаментальная статья написана раньше, чем эта статья. А у Вас «И дальше появилась…». «Когда можно спокойно сказать: число больше по mod (...).» - Я кажется Вам уже отвечал на этот бред. Ваши mod не имеют никакого смысла. Как способ проверки какая империя сильнее он может сойти. Как не оптимальный способ. Представьте, есть задача выяснить кто тяжелее. И я Вам напишу такой способ: Подходите к зеркалу. Причесываетесь. Говорите «Я ль на свете всех милее, всех румяней и белее?» Потом берете в руки гирю 16 кг. Потом встаете на весы вместе с гирей. Допустим Ваш реальный вес 70 кг. Весы покажут 86. Потом взвешиваюсь я. Делаю тоже самое. Мой вес допустим 65 кг. Весы покажут 81. У кого больше тот и тяжелее. При этом килограммы упоминаться не будут. Просто какое-то число на весах и все. Вот Вам действующий способ проверки кто из нас тяжелее. Точно такой же способ и Ваши mod. «И нет здесь ничего нового по МАТЕМАТИКЕ» - В моем способе определения кто тяжелее нет ничего нового по физике, а при способе определения кто тяжелее с вводом понятия «масса» есть новое по физике. Да и сама новая математическая игра это новое по математике.

16.08.2022, 1:36 Харт Алекс Отзыв: «Вы не пояснили одну ситуацию. Если карты - княжества, то королевства берут эти княжества по "силе". Но не может королевство брать все княжества одновременно: так устроено королевство. Нельзя воевать на несколько фронтов. Поэтому княжества берутся друг за другом. И тогда перед оформлением очередного княжества "сила" королевства меняется. И тогда ...» - Вы упускаете из виду сразу много моментов. Во-первых, это модель развития королевств, от раздробленности и до империй. Подчеркиваю – модель. Также как и игра в шахматы это модель сражения между двумя королями. Давайте с Вами попридираемся к игре в шахматы. 1) Ладья, символизирует крепость. Как так эта крепость умеет двигаться? 2) Рокировка короля символизирует собой бегство короля с поля боя в крепость. Король становится спрятанным за крепостными стенами. В реальности это бегство занимает длительное время. Как так получается, что за один ход можно сдвинуть одну пешку – пехотинца, или можно спрятать короля в крепости? В реальности эти события занимают очень разные промежутки времени. Возникает вопрос: один ход в шахматах это сколько времени если переводить в реальные события? 3) Конь – недальнобойная фигура. Слон, или офицер – дальнобойная. Что слон, что офицер разве в реальности не медленнее передвигаются, чем конь? В те времена передвижение на коне было самым быстрым видом транспорта. А в шахматах получается, что слон, или офицер двигаются намного быстрее. Как так? 4) За один ход тот или иной игрок может сдвинуть только одну фигуру (ну за исключением рокировки). А в реальности в бою могут происходить одновременно сразу много событий. Как так? Это было во-первых. Во-вторых. «И тогда перед оформлением очередного княжества "сила" королевства меняется. И тогда ...». В реальности процесс присоединения новых земель к государству может быть поэтапным. Сначала та или иная земля может зависеть от государства. И только потом она может быть включена в состав государства окончательно. Примеров тому в истории много. В данной игре, являющейся упрощенной моделью данного процесса, присоединение происходит сразу. В-третьих. «Нельзя воевать на несколько фронтов.». Возникает вопрос, сколько по времени эквивалентен один ход короля в данной игре. Хотя бы приблизительно. За три хода в данной игре король может иметь число 99. Это наибольшая мощь королевства. Дальше идет уже империя. За сколько в истории можно так развить королевство? Сложно ответить. Допустим за 150 лет. Тогда один ход в данной игре это 50 лет в реальности. За 50 лет можно присоединить несколько княжеств или вести несколько войн? С учетом сказанного в «во-вторых», за 50 лет государство может по очереди сделать зависимыми несколько княжеств (число при этом не меняется), а затем их всех сразу окончательно присоединить к своей территории (число сразу изменится с учетом присоединения сразу всех нужных карт). А поскольку в данной игре все промежуточные этапы (несколько войн по очереди в рамках 50 лет, процесс интеграции территории в государство) идут кратко в рамках одного хода короля, то и получается, что за один ход король может присоединить сразу несколько княжеств. Никаких проблем здесь нет. Возвращаюсь к «во-первых». Еще раз пишу – это модель. Приведите мне пример хотя бы одной игры, описывающей тот или иной процесс реальной жизни, в которой абсолютно все моменты игры соответствуют реальности. Хотя бы одну игру приведите.

16.08.2022, 1:40 Харт Алекс Отзыв: «Мне уже не нравится эта игра! Получается, что не обязательно в середине игры объединяться. Можно объединится трем игрокам в начале игры и "раздеть" четвертого игрока. При данной схеме подсчёта очков у четвертого игрока нет шансов на выигрыш при таком объединении!» - Раздеть четвертого игрока? Геннадий Григорьевич, я в статье раздел «Эротика» не указывал. Ближе к сути. Вы опять не догоняете несколько моментов. Когда уже придете к пониманию? Во-первых. На каком основании в начале игры трое будут объединяться против четвертого? Он им просто не нравится? Если причина такая, то этот четвертый больше не будет играть с этими договорившимися тремя. Представьте, что Дартаньян и три мушкетера играют в эту игру. И вот в начале игры три мушкетера объединятся сразу против Дартаньяна. Без всякой на то причины вытекающей из игры. Так не долго и до дуэли. Во-вторых. В правилах игры написано: «В игре могут заключаться выгодные договоренности между разными участниками. Эти договоренности могут быть самые разные. Единственное условие таких договоренностей это максимальная выгода всех их участников.». В чем выгода в самом начале игры заключить союз трем королям против четвертого? Каждый получит по 133 очка. Это много? В-третьих. Как только три короля будут обсуждать такой договор, четвертый король, поняв, что в случае заключения такого договора у него нет шансов, сразу может предложить такой договор одному из королей: тебе 75% (300 очков), а мне 25% (100 очков). Этот договор на много выгоднее чем договор трех королей. И королю кому предложат 300 очков выгоднее заключить такой договор, чем договор трех королей. В-четвертых. Полагаю, что в любой игре, где играют много игроков, возможна такая договоренность: «все против одного». Любую компьютерную игру стратегию берите. Все налетят на одного. У этого одного не будет шансов. Есть например игра в шахматы вчетвером на специальной доске. Думаю, если три игрока договорятся против четвертого, то у четвертого просто не будет шансов. Три ферзя против одного, 6 ладей против 2, и т.д. В игры «Конкурент», «Монополия» если все договорятся против одного, то у него также не будет шансов. Возвращаюсь к «во-первых». Договор королей без явной на то причины это нарушение правил игры. И если был бы турнир или чемпионат по этой игре, то таких трех договорившихся игроков судья бы наказал. «Кажется, что где-то Вы писали, что данная игра похожа на игру "Монополия". Совсем не похожа! В "Монополии", как мне помнится, остаются, как правило, два игрока, которые между собой соревнуются. И там честная игра друг против друга, а не игра одного против трех.» - Ошибаетесь. Представьте, что в монополию играют четыре игрока. И трое договариваются против четвертого. У четвертого будет шанс на победу? Просто никто в начале игры так не договаривается. И в игру «Короли» так никто договариваться не будет.

16.08.2022, 1:43 Харт Алекс Отзыв: «Допустим, на 52 картах идёт "игра" (если это называется игрой) одного против трех.» - Когда Вы последний раз держали колоду карт в руках? В стандартной колоде 54 карты. «если это называется игрой» - Для обычных людей это называется игрой, а для людей легко доказавших бинарную проблему Гольдбаха, да еще и Великую теорему Ферма, видимо нет. «одного против трех» - Почему одного против трех? Вы видели только один пример игры. Один. На основании этого судите? Вы хотели еще и этот один пример сократить. Понимаете сами всю степень своего «недогона»? Как раз очень редко игра идет с договоренностью трех королей. Бывает выигрывает один король в одиночку. И бывает выигрывают два договорившихся короля. Три договорившихся короля - это очень редкий случай. Для Вас надо не сокращать статью, а привести еще десяток примеров игры, чтобы Вы наконец это поняли. Я Вам уже писал: поиграйте сами в эту игру несколько раз. Тогда понимание к Вам придет скорее. Пока что у Вас его нет. «А скольким игрокам надо объединиться, чтобы выиграть на 104 картах, на 108 картах, и т. д.? Сказали А, говорите Б.» - Вы даже на одной колоде не поняли ничего. А уже пишите про две колоды… На двух колодах предположу, что самым частым сценарием будет победа трех-четырех так или иначе договорившихся королей. Но подчеркну. Для Вас надо обязательно все подчеркивать. Вы же не поймете с первого раза. Эта договоренность трех-четырех королей будет не случайной и не в начале игры. А действительно взаимно выгодной и максимально выгодной. Не все короли по этой договоренности могут получить одинаково. И скорее всего будет сначала союз двух королей. Потом два короля объединятся еще с одним или двумя. Для такого объединения будут объективные причины. Что и требуют правила игры.

16.08.2022, 1:46 Харт Алекс Отзыв: «Мне совершенно не нравится эта статья. Автор показал, что с помощью данной игры три игрока, договариваясь, обыгрывают четвертого. При этом других вариантов быть не может. А эти три игрока как бы друг друга не знают. Это что-то напоминает ... Поэтому я против публикации такой статьи.» - Своей новой рецензией человек, «доказавший» бинарную проблему Гольбаха и Великую теорему Ферма, в очередной раз показал насколько он далек от понимания. Просто нет слов. Где я писал «При этом других вариантов быть не может.» ? Откуда это следует? В предыдущих ответах я ответил уже на этот бред. Повторяться не хочется. Удивляет одно. И этот человек пишет о сокращении статьи? Чтобы он понял игру, ему нужна дюжина подробнейшим образом описанных партий в эту игру. Тогда он наконец поймет, что договоренность трех королей это большая редкость. Кроме того, он поймет, что любая договоренность королей чем-то обусловлена. Игрой. А не кто-то кому-то не нравится. Ему надо купить в магазине колоду карт и играть, играть, играть, играть, играть, играть, играть, играть, играть, играть в игру «Короли». Тогда есть надежда, что понимание к нему придет. Пока оно у него на ничтожном уровне. Печально.

16.08.2022, 7:47 Усов Геннадий Григорьевич Отзыв: Автор много говорит о чём угодно, только не о задаче. У Вас всего 400 очков. Чтобы победить того, у кого 99 очков, необходимо набрать 199. А чтобы набору таких очков никто не мешал, необходимо, чтобы другие два игрока имели по 99 очков и "сторожили" четвертого. То есть, 3 игрока "в теме".

16.08.2022, 8:16 Усов Геннадий Григорьевич Отзыв: Уточню про "сдерживание". Есть 3 игрока, которые договорились. 1-й остановился на 99 очках. 2-й игрок "сливает" свои очки в пользу 3-го игрока, при этом у 2-го игрока количество очков стремится к 0, а у 3-го игрока количество очков стремится к 199. Если у 3-го игрока будет 199 очков, то этот игрок будет отбирать очки у 4-го гроки. И одновременно 1-й игрок отбирает очки у 4-го игрока. Вот Вам схема работа "на троих".

16.08.2022, 10:50 Харт Алекс Отзыв: Я позже отвечу Вам, а Вы пока постарайтесь ответить на все вопросы к Вам.

16.08.2022, 12:14 Усов Геннадий Григорьевич Отзыв: При этом, "шакалы", которые 1-й и 3-й игроки, будут рвать империю 4-го игрока таким образом, чтобы последнеё цифрой у 4-го игрока было число, меньшее их последних цифр. При этом, они по договоренности, "создадут" ХОРОШЕЕ последнюю цифру у 2-го игрока, чтобы ещё сильнее "рвать" 4-го игрока. А 4-й игрок будет просто смотреть, потому что он не может ходить, так как у него ОЧЕНЬ МАЛЕНЬКАЯ последняя цифра. (У Вас нет правила обязательного хода!) И это Вы называете математической ИНТЕЛЛЕКТУАЛЬНОЙ игрой?

16.08.2022, 15:10 Усов Геннадий Григорьевич Отзыв: "Я позже отвечу Вам, а Вы пока постарайтесь ответить на все вопросы к Вам." - Обычно, рецензент или оппонет задают вопросы по статье, на которые необходимо отвечать автору статьи. В ваших последних ответах много воды, но нет конкретного короткого ответа на поставленные вопросы в виде одного - двух предложений.

16.08.2022, 15:13 Усов Геннадий Григорьевич Отзыв: "Эта договоренность трех-четырех королей будет не случайной и не в начале игры. А действительно взаимно выгодной и максимально выгодной. Не все короли по этой договоренности могут получить одинаково. И скорее всего будет сначала союз двух королей. Потом два короля объединятся еще с одним или двумя. Для такого объединения будут объективные причины. Что и требуют правила игры." А кто Вам сказал, что они заранее не договорились. Уже в процессе игры они (трое) решают: кто будет по 99, кто малым - подъигрывать, а кто стремится к 199.

17.08.2022, 0:40 Харт Алекс Отзыв: «Автор много говорит о чём угодно, только не о задаче.» - Ничего себе «о чём угодно, только не о задаче». На какие вопросы я Вам не ответил? «о чём угодно, только не о задаче». - Приведите конкретные примеры. «У Вас всего 400 очков. Чтобы победить того, у кого 99 очков, необходимо набрать 199. А чтобы набору таких очков никто не мешал, необходимо, чтобы другие два игрока имели по 99 очков и "сторожили" четвертого. То есть, 3 игрока "в теме".» - Опять не догоняете. Чтобы победить того у кого 99 в большинстве случаев достаточно договоренности двух королей. Кроме того, того у кого 99 может победить и один король, но этот путь рисковый. Подробнее напишу только про двух королей. Допустим надо победить короля №1. У него 99. Победить его хочет король №2. У него тоже 99. Он и сдерживает короля №1. Королю №2 остается только договориться с одним из королей, желательно с тем, кто посильнее, чтобы тот расширялся до числа 199.

17.08.2022, 0:42 Харт Алекс Отзыв: «Уточню про "сдерживание". Есть 3 игрока, которые договорились. 1-й остановился на 99 очках. 2-й игрок "сливает" свои очки в пользу 3-го игрока, при этом у 2-го игрока количество очков стремится к 0, а у 3-го игрока количество очков стремится к 199.» - А зачем договариваться с игроком 2 чтобы тот сливал очки? Если 2-й игрок слабее 3-его, то он вынужден будет сливать очки. Его никто не спросит. Зачем его брать в долю, чтобы потом делиться с ним победой? «Если у 3-го игрока будет 199 очков, то этот игрок будет отбирать очки у 4-го гроки. И одновременно 1-й игрок отбирает очки у 4-го игрока. Вот Вам схема работа "на троих".» - Это схема работы «на двоих».

17.08.2022, 0:44 Харт Алекс Отзыв: «При этом, "шакалы", которые 1-й и 3-й игроки, будут рвать империю 4-го игрока таким образом, чтобы последнеё цифрой у 4-го игрока было число, меньшее их последних цифр. При этом, они по договоренности, "создадут" ХОРОШЕЕ последнюю цифру у 2-го игрока, чтобы ещё сильнее "рвать" 4-го игрока. А 4-й игрок будет просто смотреть, потому что он не может ходить, так как у него ОЧЕНЬ МАЛЕНЬКАЯ последняя цифра.» - Надеюсь Вы уже поняли, что Ваш сценарий маловероятен. Вероятен сценарий договоренности двух игроков. Вам следует понять, что Ваш сценарий существует только в теории. Вы не играли в эту игру. У Вас только теоретические рассуждения. Абсолютно не верные. А я имею практический опыт в игре. У меня есть и теоретические рассуждения, и практический опыт. «У Вас нет правила обязательного хода!» - А зачем восклицательный знак? Объясните, зачем нужно правило обязательного хода? Что оно дает? В конце концов, право короля расширяться или нет остается его правом. «И это Вы называете математической ИНТЕЛЛЕКТУАЛЬНОЙ игрой?» - Вы же поняли, что Вы снова не догнали с договоренностью трех королей? Да, я это называю математической ИНТЕЛЛЕКТУАЛЬНОЙ игрой. Повторяю. У Вас в голове существуют только неверные теоретические рассуждения, ничем не подтвержденные. А мой практический опыт говорит о том, что думать в этой игре нужно ой-ой-ой.

17.08.2022, 0:46 Харт Алекс Отзыв: «Обычно, рецензент или оппонет задают вопросы по статье, на которые необходимо отвечать автору статьи.» - Я отвечаю на все Ваши вопросы. Вы же большую часть моих вопросов динамите. Видно вопросы слишком неудобные для Вас. «В ваших последних ответах много воды, но нет конкретного короткого ответа на поставленные вопросы в виде одного - двух предложений.» - Ничего себе «воды». Если стенке говорить все что угодно, самую умную фразу, то для нее конечно это все остается водой. Я Вам пишу подробно, с примерами из жизни, все для Вас, только чтобы Вы поняли.

17.08.2022, 0:48 Харт Алекс Отзыв: «А кто Вам сказал, что они заранее не договорились.» - Ну знаете ли. Так тогда в любой игре, где играют 3 и более игрока кто-то еще до начала игры может договариваться. «Уже в процессе игры они (трое) решают: кто будет по 99, кто малым - подъигрывать, а кто стремится к 199.» - Нужны еще пояснения, что Ваш сценарий абсурден? Кроме того, Вы в очередной раз продинамили, а я писал в предыдущих ответах следующее. Что цель не просто выиграть, а выиграть, набрав максимальное количество очков. Если договорились три короля, то они получат по 133 очка. А надо понимать, что изначально по идее на каждого короля выделяется 100 очков. Одна масть – сумма карт одной масти – 100 очков. 4 короля. Итого 400 очков. Т.е. по справедливости если каждому поровну, то это по 100 очков. А здесь они получат по 133. Накрутка 33 очка всего. А если король выигрывает в одиночку, то он берет 400 очков, т.е. накрутка 300 очков. Есть разница? Нет никакого смысла делиться очками с королями без на то необходимости. И я уже писал, что как только будет озвучиваться договоренность трех королей, то 4-ый сразу может предложить одному из них договор 75% на 25%, являющийся более выгодным для короля кому предлагается 75%. Ваша фраза «А кто Вам сказал, что они заранее не договорились.» это из области фантастики. И много Вы играли в игры с большим количеством участников, где вот так договаривались: «Давай все договоримся и оставим Ваньку»?

17.08.2022, 8:06 Усов Геннадий Григорьевич Отзыв: "Допустим надо победить короля №1. У него 99. Победить его хочет король №2. У него тоже 99. Он и сдерживает короля №1. Королю №2 остается только договориться с одним из королей, желательно с тем, кто посильнее, чтобы тот расширялся до числа 199." - Ошибаетесь! Король №2 должен договориться с королем №4, чтобы он был "ванькой". Король №3 будет брать очки у "ваньки", чтобы достичь значения 199.

17.08.2022, 8:09 Усов Геннадий Григорьевич Отзыв: "Надеюсь Вы уже поняли, что Ваш сценарий маловероятен." - Так Вы этот сценарий описали в статье! Правда, при этом Вы говорите о высоком, о некоторых договорённостях.

17.08.2022, 8:18 Усов Геннадий Григорьевич Отзыв: "Вероятен сценарий договоренности двух игроков." - У Вас в статье "Король бубен будет договариваться или с королем крестей, или с королем виней. " и "Король червей становится аутсайдером игры, и для него единственный вариант хоть что-то получить, это договариваться с другими королями. " Здесь Вы грамотно пишите: есть варианты. То есть, Вы приглашаете 4-го к уже имеющимся 3-м игрокам и говорите ему: ЕСТЬ ВАРИАНТЫ. То есть, Вы подготовили игру, правила в которой позволяют "обобрать" этого 4-го игрока.

17.08.2022, 8:21 Усов Геннадий Григорьевич Отзыв: "Я Вам пишу подробно, с примерами из жизни, все для Вас, только чтобы Вы поняли." - А зачем Вы пишите из жизни, тем более из моей жизни? Вы должны отвечать только по статье, не нужны примеры из других источников.

17.08.2022, 8:25 Усов Геннадий Григорьевич Отзыв: "И много Вы играли в игры с большим количеством участников, где вот так договаривались: «Давай все договоримся и оставим Ваньку»?" - А разве бывают серьезные игры в карты, где нет договорённости между игрками. Только в тех играх как бы нельзя офицально договариваться. А в Вашей игре Вы провозглашаете открыто: договаривайтесь против 4-го (Ваньки).

17.08.2022, 11:20 Харт Алекс Отзыв: «Ошибаетесь! Король №2 должен договориться с королем №4, чтобы он был "ванькой". Король №3 будет брать очки у "ваньки", чтобы достичь значения 199.» - Зачем договариваться с королем №4, чтобы он был «Ванькой»? Если он слабый, то он уже «Ванька». Король №3 спокойно будет расширяться до 199, отбирая у него территорию.

17.08.2022, 11:22 Харт Алекс Отзыв: «Так Вы этот сценарий описали в статье! Правда, при этом Вы говорите о высоком, о некоторых договорённостях.» - Во-первых, я описал не этот сценарий. Вы уже забыли, что король крестей и король бубей договорились делить пополам победу задолго до того, как один из них набрал 99 очков? Во-вторых, я потому и описал этот пример в статье, потому что он редкий, не стандартный, когда почти в начале игры есть договоренность между королями. Это может быть только если два короля находятся рядом. Как раз описываемый в статье случай. Поэтому это совсем другой сценарий.

17.08.2022, 11:23 Харт Алекс Отзыв: «Здесь Вы грамотно пишите: есть варианты. То есть, Вы приглашаете 4-го к уже имеющимся 3-м игрокам и говорите ему: ЕСТЬ ВАРИАНТЫ.» - Не понял о чем Вы. «То есть, Вы подготовили игру, правила в которой позволяют "обобрать" этого 4-го игрока.» - Я хочу напомнить, что этот 4-й игрок в приводимой в статье партии первым достиг числа 99. Т.е. он был самым сильным королем. И для него были варианты. Он мог не заключать договоров, т.е. понадеяться на свою силу, что удастся победить остальных королей в одиночку. Или же заключить договор хотя бы с тем же королем червей. В статье описан первый вариант. А их по игре всегда много. Если я играл бы в расклад из статьи еще раз, то скорее всего я играл бы по-другому и итог игры был бы совсем иной. По идее, как только король крестей и король бубей заключили договор, двум другим королям также следовало бы заключить договор. Это ошибка короля виней, что этот договор не был заключен. И такое может быть. «То есть, Вы подготовили игру, правила в которой позволяют "обобрать" этого 4-го игрока.» - Если этот 4-ый игрок понадеется на свою силу, будет считать что в одиночку всех захватит, то да, он может за это поплатиться.

17.08.2022, 11:23 Харт Алекс Отзыв: «А зачем Вы пишите из жизни, тем более из моей жизни? Вы должны отвечать только по статье, не нужны примеры из других источников.» - Что делать, если Вы не всегда понимаете.

17.08.2022, 11:25 Харт Алекс Отзыв: «А разве бывают серьезные игры в карты, где нет договорённости между игрками. Только в тех играх как бы нельзя офицально договариваться.» - Причем тут игры в карты? Я пишу про любые игры с большим количеством игроков. В моей игре тоже нельзя договариваться как Вы изначально писали. Еще до игры троим договориться против четвертого. Так нельзя. В процессе игры взаимовыгодные договоренности могут быть. При этом правило остается, что каждый стремится не просто выиграть, а максимально расширить свою территорию. Договор трех королей дает мало добавки к территории. Этому договору можно противопоставить более выгодные договора. «А в Вашей игре Вы провозглашаете открыто: договаривайтесь против 4-го (Ваньки).» - Приехали. Я из кожи вон лезу, доказывая Вам, что договор трех королей не эффективен. Только в очень редких случаях он возможен. Например, как в описываемой в статье партии, когда два короля находятся рядом и в самом начале игры вынуждены договариваться. А я оказывается открыто провозглашаю: «Давайте все против Ваньки». Нет, нет и нет. Я так не провозглашаю. Вы чего.

17.08.2022, 13:16 Усов Геннадий Григорьевич Отзыв: "Зачем договариваться с королем №4, чтобы он был «Ванькой»? Если он слабый, то он уже «Ванька». " - Так ваши уже решили заранее, что он будет "ванькой" (тот, кто окажется слабым).

17.08.2022, 13:19 Усов Геннадий Григорьевич Отзыв: " «Здесь Вы грамотно пишите: есть варианты. То есть, Вы приглашаете 4-го к уже имеющимся 3-м игрокам и говорите ему: ЕСТЬ ВАРИАНТЫ.» - Не понял о чем Вы. " - Это о том, что приглашается 4-й, которого хотят обобрать, и ему говорят, что есть ВАРИАНТЫ, которые позволяют ему выиграть.

17.08.2022, 13:21 Усов Геннадий Григорьевич Отзыв: "Еще до игры троим договориться против четвертого. Так нельзя. " - А кто сказал, что нельзя. Этого в правилах НЕТ!

17.08.2022, 13:23 Усов Геннадий Григорьевич Отзыв: "...каждый стремится не просто выиграть, а максимально расширить свою территорию." - Об этом рассуждать можете сколько угодно. На кону более важная цель - обобрать 4-го.

17.08.2022, 23:22 Харт Алекс Отзыв: «Так ваши уже решили заранее, что он будет "ванькой" (тот, кто окажется слабым).» - Кто решил? Когда решил?

17.08.2022, 23:22 Харт Алекс Отзыв: «Это о том, что приглашается 4-й, которого хотят обобрать, и ему говорят, что есть ВАРИАНТЫ, которые позволяют ему выиграть.» - Куда приглашается 4-й? Какие варианты?

17.08.2022, 23:23 Харт Алекс Отзыв: «"Еще до игры троим договориться против четвертого. Так нельзя. " - А кто сказал, что нельзя. Этого в правилах НЕТ!» - А без правил Вам это не понятно? В правилах также не написано, что нельзя например у игрока брать его короля, рвать его и говорить: «я так разрушил столицу его империи». Можете привести пример хотя бы одной игры, где можно было бы заранее всем договориться против одного игрока по причине, что его зовут «Ванька»?

17.08.2022, 23:24 Харт Алекс Отзыв: «Об этом рассуждать можете сколько угодно. На кону более важная цель - обобрать 4-го.» - А чем 4-ый хуже 3-го, 2-го или 1-го? Четвертого зовут «Ванька», да? Это единственное, чем он «хуже»?

17.08.2022, 23:49 Харт Алекс Отзыв: Еще раз попробую. Рассмотрим гипотетическую игру. (Специально для Вас повторяю, что любая договоренность заранее против «Ваньки» исключена.) Примерно такой сценарий игры. Король №1 набирает 99 очков. Затем король №2 набирает 99 очков. Допустим король №3 и король №4 набирают 79 очков. Это на каком-то раунде игры. Какие варианты договоренностей могут последовать? Самый простой 1-ый вариант: королям №1 и №2 договориться поделить победу пополам. (Специально для Вас пишу, что не факт что эта победа сто процентов произойдет, так как короли №3 и №4 тоже договорятся в таком случае, и мало ли чего. Хотя конечно перевес будет на стороне королей №1 и №2.) Минус такой договоренности такой, что короли №1 и №2 оба получат по 200 очков, а всегда хочется быть лучшим, всегда хочется получить больше остальных. Поэтому варианту 1 можно найти предпочтение в варианте 2: король №1 договорится с королями №3 и №4 заключить договор и поделить победу так: ему 200 очков, а двум остальным королям по 100. Но если будет озвучиваться этот вариант, то король №2 предложит королям №3 и №4 более выгодный вариант 3: ему 150 очков, а двум остальным королям по 125 очков. Тогда королю №1 придется предложить уже крайний вариант 4: ему 134 очка, а двум остальным королям по 133 очка. И к чему мы пришли? Король №1 хотел быть лучшим, набрать больше всех очков, 200 на 200 его не устроило, и он пришел к варианту 134, 133, 133? Но очевидно, что вариант 200 на 200 лучше, чем вариант 134, 133, 133. Там он делил в равной доле победу с одним королем, а здесь с двумя. Да и очков получит меньше. Поэтому вариант 1 будет предпочтительнее. Но если уж захочется быть лучшим, то будут рассматриваться такие варианты: король №1 заключит договор с королем №3, победа будет делиться например так: 300 очков королю №1, 100 очков королю №3. Но в этом случае автоматически будет заключен аналогичный договор между королями №2 и №4. Такая игра пара на пару более чем интересна. (Специально для Вас уточняю. Что рассмотрен общий случай. Без учета какой король где находится на игровом поле, какой король ходит первым, вторым и т.д. А эти факторы более чем сильно влияют на договоренности.) Ваш вариант – «сообразим на троих» - никому интересен не будет. И я Вам напомню, что приводимый в статье вариант договоренности трех королей это другой сценарий. Там два короля договорились почти в начале игры из-за того, что находятся близко друг к другу. Потом они заключили неравный договор с третьим королем. Это не вариант 2, 3 или 4, которые я здесь описал. Это совсем иной сценарий. Кстати возможна еще такая вариация игры «Короли» - пара на пару. (По аналогии с игрой в дурака пара на пару.) Тогда никаких договоренностей в этой игре не будет. По-сути будет действовать изначальная договоренность пара на пару.

18.08.2022, 8:15 Усов Геннадий Григорьевич Отзыв: "«Это о том, что приглашается 4-й, которого хотят обобрать, и ему говорят, что есть ВАРИАНТЫ, которые позволяют ему выиграть.» - Куда приглашается 4-й? Какие варианты?" - Объясняю. Еду в купе поезда, заходит сосед и говорит: "Не хотите сыграть в новую, математическую, интеллектуальную игру «Империи», уже есть трое, нужен 4-й. Ставка будет небольшой, для интереса.

18.08.2022, 8:19 Усов Геннадий Григорьевич Отзыв: "Еще раз попробую... " - Вы можете сколько угодно оперировать разными вариантами очков, но окончательно будет следующее: 1-й набирает 99 очков, 2-й "разрешает" 3-му отбирать у него очки, 3-й набирает 199 очков (при этом он не должен "контачить" с 4-м игроком, это для 3-х игроков решаемо). Вот и всё для 4-го игрока.

18.08.2022, 10:45 Харт Алекс Отзыв: «Объясняю. Еду в купе поезда, заходит сосед и говорит: "Не хотите сыграть в новую, математическую, интеллектуальную игру «Империи», уже есть трое, нужен 4-й. Ставка будет небольшой, для интереса.» - Так. И?

18.08.2022, 10:48 Харт Алекс Отзыв: «Вы можете сколько угодно оперировать разными вариантами очков, но окончательно будет следующее: 1-й набирает 99 очков, 2-й "разрешает" 3-му отбирать у него очки, 3-й набирает 199 очков (при этом он не должен "контачить" с 4-м игроком, это для 3-х игроков решаемо). Вот и всё для 4-го игрока.» - Подождите. Подождите. Можно поподробнее? В какой момент этот договор будет заключен? Из Вашего примера я понял, что 1-й и 4-й имеют по 99 очков. Что будет потом? Кто как договорится?

18.08.2022, 11:02 Усов Геннадий Григорьевич Отзыв: "Так. И?" - "Подождите. Подождите. Можно поподробнее? В какой момент этот договор будет заключен? Из Вашего примера я понял, что 1-й и 4-й имеют по 99 очков. Что будет потом? Кто как договорится?" - Это есть продолжение после разговора в купе. 4-й - тот из купе. Другие три игрока уже для себя заключили соглашения, а в игре будут говорить 4-му игроку, что заключать договорённости лучше с другими игроками, поскольку у 4-го игрока трудная ситуация.

18.08.2022, 11:57 Харт Алекс Отзыв: Вообще не понятно то, что Вы описали. Если Вы о том, что в купе трое изначально договорились и ищут четвертого «Ваньку», то я Вам уже ответил. В чем смысл? Если это игра на деньги, то Вас не учили, что на деньги нельзя играть с незнакомыми людьми? Вы так стали бы играть в покер на деньги с тремя попутчиками в поезде, которые к тому же друг друга знают, одна компания? Может там сидят три шулера, которые ездят по поездам и облапошивают соседей по купе? Если это игра не на деньги, а на очки. То даже если они изначально договорились между собой, то в процессе игры это будет видно. Этот 4-ый игрок предложит им более выгодный договор, а они от него откажутся и вместо этого договорятся втроем против него на менее выгодных условиях. Ну тогда всё понятно, и он больше не будет с ними играть. А если эта игра была бы на турнире или чемпионате, то судья и вовсе наказал бы троих договорившихся, если этот договор был менее выгоден, чем другой предлагавшийся.

18.08.2022, 12:10 Усов Геннадий Григорьевич Отзыв: "... то судья и вовсе наказал бы троих договорившихся, если этот договор был менее выгоден, чем другой предлагавшийся." - Что, уже судья решает о том, кому с кем заключать договор? Почему я не могу заключить договор, который пока менее выгоден для меня? Но зато, через несколько ходов, я буду в плюсе!

18.08.2022, 12:40 Харт Алекс Отзыв: «Что, уже судья решает о том, кому с кем заключать договор? Почему я не могу заключить договор, который пока менее выгоден для меня? Но зато, через несколько ходов, я буду в плюсе!» - Вы будете в плюсе, а двое договорившихся с Вами будут в минусе. Вы им предложите «сообразить на троих» по 133 очка (одному 134, не суть). А я этому договору противопоставлю два договора. Первый. Вам предложу, Геннадий Григорьевич, у Вас 99 очков и у меня. Зачем Вам договариваться с ними по 133 очка, когда давайте с Вами поделим победу пополам, по 200 очков. Вы будете в большем плюсе. Второй. Я могу предложить двум остальным такой договор. Скажу им. Геннадий Григорьевич вам предлагал по 133 очка каждому, а я вам предложу больше. Мне 100, а вам по 150. Тогда они со мной договорятся против Вас. А если от второго договора эти двое откажутся, то судья их накажет. Потому что им предлагался аналогичный более выгодный договор, а они отказались. А Вас судья накажет, если Вы откажетесь от договора 1 в пользу своего «сообразим на троих», так как он менее выгоден для Вас.

18.08.2022, 13:35 Усов Геннадий Григорьевич Отзыв: "Если это игра на деньги, то Вас не учили, что на деньги нельзя играть с незнакомыми людьми?" - Вы претендуете на "Спорт", а в спорте всегда незнакомые люди, и всегда деньги в том или ином виде. Это только дома родня, и то...

18.08.2022, 14:07 Харт Алекс Отзыв: «Вы претендуете на "Спорт", а в спорте всегда незнакомые люди, и всегда деньги в том или ином виде. Это только дома родня, и то...» - Вот именно. Всегда незнакомые люди. И деньги. Там важно думать только о максимальном собственном расширении, а не о том, чтобы путем менее выгодного для себя договора обыграть какого-то конкретного игрока, которого Вы даже не знаете.

18.08.2022, 16:59 Усов Геннадий Григорьевич Отзыв: "Там важно думать только о максимальном собственном расширении, " - А что даёт собственное расширение? Когда на кону общая победа (3 х 1). А если ставка на игру не связана с количеством очков, а с конкретными деньгами, то лучше играть сообща: стабильный выигрыш.

18.08.2022, 17:36 Харт Алекс Отзыв: Допустим на кону 400 тыс. руб. За каждое набранное очко по итогу игры Вы получаете 1 тыс. руб. Как Вам выгоднее сыграть: заключить со мной договор (у нас обоих по 99 очков) разделив победу пополам, т.е. по 200 очков каждому, или "сообразить на троих" с другими двумя королями (у них не 99 очков, они слабее) по 133 каждому? В первом случае Вы получите 200 тыс. руб. Во втором - 133 тыс. руб. "А что даёт собственное расширение?" - Собственное расширение это и есть максимальное количество набранных очков по итогу игры, которые потом конвертируются в деньги. Не временное расширение. "А если ставка на игру не связана с количеством очков, а с конкретными деньгами, то лучше играть сообща: стабильный выигрыш." - Как раз связана. Сколько очков набрал по итогу игры, столько и получил. Если выиграл всех в одиночку, то получишь 400 тыс. руб. Если пополам разделил победу по договору 200 и 200, то каждому по 200 тыс. руб. Просто выиграть это одно. Важно выиграть с максимальным количеством очков, а это и есть максимальное расширение. Оно может быть достигнуто собственными усилиями или благодаря договору, это уже другой вопрос.

18.08.2022, 19:39 Усов Геннадий Григорьевич Отзыв: "Допустим на кону 400 тыс. руб." - Далее можно не считать очки и выигрыши. 400 тыс. руб. получат три игрока, которые договорились. 4-ый игрок ничего не получит, так как он проиграл (а он всегда при такой ситуации проиграет). Три игрока заключили официальное соглашение о разделе выигрыша в процессе игры согласно правилам игры. Официально они напишут какие-то ставки, а на самом деле они договорились на свои ставки перед игрой. При этом эти три игрока должны придерживаться правил игры и играть против 4-го игрока тоже согласно правилам игры. Так что про максимальное количество можно говорить сколько угодно - выигрыш 400 тыс. руб. уже поделён между тремя игроками до игры.

19.08.2022, 1:20 Харт Алекс Отзыв: Ваш тезис такой: раз закон всё равно можно придумать как безнаказанно нарушить, то закон не нужен. Правильно я услышал Ваш посыл? Да и в спорте тоже самое. Зачем проводить соревнования и проверять кто быстрее бегает, когда кто-то может на анаболиках всех обогнать. Наверное для этого и есть антидопинговая служба. Но очевидно и ее придумывают люди как обойти. На досуге подумайте об этом. Вернемся к нашим баранам. По Вашему чемпионат так и будет проходить, что все друг друга знают, и так легко могут договориться заранее? И там будут участвовать только четыре игрока во всем чемпионате? Допустим даже всё же три игрока договорились заранее. И как раз они играют с 4-ым «Ванькой» в одной партии. И они так и будут сидеть с колодой карт? Или всё же это будет происходить на компьютерах в электронной версии этой игры? Наверное, на компьютерах. В этом случае будет даже не понятно, кто за какого короля играет, кто есть кто. Кто там «Ванька» не понятно. Каждый сидит в отдельном помещении. Никакие устные переговоры невозможны. Мобильная связь отключена. Договоры могут предлагаться только через электронный интерфейс игры. За игрой следят судьи. Всё по взрослому. Допустим даже и это обошли. Поняли кто «Ванька». Какие конкретно официальные ставки они поставят, чтобы не быть заподозренными судьями в сговоре? Допустим организаторы чемпионата придут к выводу, что даже это можно обойти. Ну тогда сделают, что каждый участник чемпионата будет играть с компьютерными игроками. Т.е. в партии участвует один человек и три компьютера. Чемпионат будет состоять естественно не из одной партии на одного человека. Допустим из 10. По итогу сыгранных 10 партий каждый будет иметь какое-то набранное количество очков. Далее кто больше набрал, т.е. лучше обыгрывал компьютеров, тот и победил в чемпионате. С компьютерами естественно тоже можно будет заключать договоры, но компьютер будет договариваться только на максимально выгодных для себя условиях, согласно правилам игры.

19.08.2022, 6:26 Усов Геннадий Григорьевич Отзыв: Ваш посыл: "Такого не может быть, много честных игроков, и т.д." Проблема Вашей игры в том, что, как я раньше говорил, Вы РАЗРЕШИЛИ ОФИЦИАЛЬНО строить блоки 3-х игроков против 4-го игрока. Такого ещё в спорте не было! Напишите об этом в статье, как о НАУЧНОЙ НОВИЗНЕ. Вы можете сколько угодно говорить, что всё будет хорошо, по честному, но я не верю. Поскольку Вы пока в разделе МАТЕМАТИКА, то ДОКАЖИТЕ то, что игра будет по честному ВСЕГДА.

19.08.2022, 11:38 Харт Алекс Отзыв: «Ваш посыл: "Такого не может быть, много честных игроков, и т.д."» - Это не мой посыл. Я Вам описал как будет примерно проходить чемпионат. Все по взрослому. Обойти службу контроля практически нереально. А для таких умников как Вы, любящих «соображать на троих», наказание – дисквалификация, еще и огромный штраф. Вам того надо? «Проблема Вашей игры в том, что, как я раньше говорил, Вы РАЗРЕШИЛИ ОФИЦИАЛЬНО строить блоки 3-х игроков против 4-го игрока.» - Вы забываете про главное требование: «Единственное условие таких договоренностей это максимальная выгода всех их участников.» «Такого ещё в спорте не было! Напишите об этом в статье, как о НАУЧНОЙ НОВИЗНЕ.» - Так я молодец, что предлагаю, что-то новое? «Вы можете сколько угодно говорить, что всё будет хорошо, по честному, но я не верю.» - «Я не верю.» - Я помню Вы и в доказательстве бинарной проблемы Гольдбаха писали: «Я не верю, что это возможно». «Поскольку Вы пока в разделе МАТЕМАТИКА, то ДОКАЖИТЕ то, что игра будет по честному ВСЕГДА.» - Я же уже Вам столько доказательств привел. И Вы все их благополучно продинамили. Осталось только «я не верю». Давайте из последних. «Какие конкретно официальные ставки они поставят, чтобы не быть заподозренными судьями в сговоре?» - Ответа от Вас не было. Было только, что они договорились и выиграли. А подробно как их договор прошел мимо судьи Вы не написали. По сути Вы предложили примерно такой вариант. Чемпионат по шахматам. Каспаров хочет быть победителем. Всего 50 участников. Каспаров привел 49 договорившихся с ним подставных участников, которые ему поддаются в игре. Он всех их обыгрывает и становится чемпионом мира. И потом с меня же требуете доказательства, что такой сценарий невозможен. Вам самому не понятна абсурдность такого сценария? Ладно. Я жду ответа только на один вопрос пока. Как трое договорившихся смогут победить четвертого на чемпионате? Какой договор они предложат, чтобы не быть заподозренными в сговоре?

19.08.2022, 23:59 Усов Геннадий Григорьевич Отзыв: "Обойти службу контроля практически нереально. " - В Вашей игре появляется служба контроля, а Вы про неё не сказали в своей статье. Просьба пояснить её функции, обязанности и какие будут наказания от этой службы. И самое главное: на основании какой методики эта служба будет отличать официальные договорённости игроков (по нашему - сговор) от неофициального сговора, на основании которого появились официальные договорённости.

21.08.2022, 0:36 Харт Алекс Отзыв: «В Вашей игре появляется служба контроля, а Вы про неё не сказали в своей статье.» - Простите, она появляется не в игре, а в гипотетической организации, которая проводит чемпионат по этой игре. Описывать структуру данной организации не являлось целью данной статьи. «Просьба пояснить её функции, обязанности и какие будут наказания от этой службы.» - А Вы сами не представляете как проходят чемпионаты или олимпийские игры? По Вашему никто не следит за тем, чтобы олимпийские объекты соответствовали стандартам, чтобы игры проводились по честному, с соблюдением всех правил? Если в боксе один ударил второго и он свалился, то не был ли этот удар запрещенным? Никто ничего не отслеживает, делай что хочешь, главное выиграть, так что ли у Вас? А я сейчас Вам должен расписать все нарушения и наказания какие будут со стороны службы контроля чемпионата по игре в «Империи»? Не явился на чемпионат – лишаешься участия в аналогичном чемпионате через год. Оскорбил судью – дисквалификация на три года. Вот это я должен Вам расписать? Видно Вас опять куда-то унесло не туда. Бывает. Я уже привык. «И самое главное: на основании какой методики эта служба будет отличать официальные договорённости игроков (по нашему - сговор) от неофициального сговора, на основании которого появились официальные договорённости.» - Я уже отвечал Вам на этот вопрос. Если был заключен договор явно для себя проигрышный, т.е. из нескольких договоров игрок согласился на явно не выгодный для себя договор, то можно заподозрить что этот игрок кому-то подыгрывает.

21.08.2022, 0:55 Харт Алекс Отзыв: Мне кажется, что Вы полностью ушли куда-то не в ту степь. Вы запутались окончательно. Первое. Вы как будто не представляете, как может проходить подобный чемпионат. Участников явно не четыре. А десятки, а может и сотни, из разных стран. Как там кто договорится? Второе. Чтобы чемпионат был проведен честно, то основная проблема не в том, что кто-то договорится заранее, а в том, чтобы у всех были одинаковые условия. У кого-то король будет в углу, у кого-то в центре. Один ходит первый, другой последний. Поэтому вряд ли он будет проходить так, что участники играют друг с другом. Скорее каждый участник будет играть с компьютерами, и у каждого участника будут точно такие же расклады как у всех. Примерно так проходил один чемпионат в преферанс, о котором мне рассказывали. Каждый сидел за компьютером и играл с компьютерными игроками в одни и те же расклады что и все. Кто больше набрал очков, тот и выиграл чемпионат. Третье. Даже если игроки будут играть друг с другом в партиях по 4 человека. И в каких-то партиях будут заранее договариваться против кого-то. И что? Тайные договоры могут быть везде. Вы знаете точно, что у Каспарова и Карпова не было тайного договора, чтобы Карпов поддавался Каспарову, а Карпов был просто подставным игроком? Вы знаете точно, что в чемпионатах по футболу нет тайных договоров, что кто-то кому-то проиграет? Считайте, что в футболе есть изначальные договоры 11-ти игроков, против других 11-ти игроков. Это официально. А Вы уверены, что 5 игроков из одной команды на самом деле не подыгрывают команде противника, поскольку у тех есть тайная договоренность? Мы об этом не узнаем. Но это не умаляет ни одной из игр. А у Вас получается, что раз можно в игре «Империи» заранее договориться, то это не игра. Вы еще не поняли, что заранее о чем-то можно договориться где угодно? Кроме того, я Вам уже давно писал про проведение чемпионата с игрой с компьютерами. Вы это благополучно продинамили и продолжаете писать то, что к сути не относится. Вы писали, что это единственная игра в спорте, где вообще есть договоры с кем-то. Отлично. Подоговаривайтесь с компьютерами. В их программы не будет зашит код, что надо договориться обязательно против вон того игрока, потому что его зовут «Ванька». Компьютерных игроков устроят только выгодные договоры. Каждый компьютер будет играть только для того, чтобы он сам получил максимальное количество очков. Какие проблемы? Если придумали как провести чемпионат по преферансу, то по Вашему нет никаких возможностей его провести для игры «Империи»? Вы подумайте сами на досуге, как мог бы провестись такой чемпионат с учетом того, что я Вам написал.

21.08.2022, 8:37 Усов Геннадий Григорьевич Отзыв: "Если был заключен договор явно для себя проигрышный, т.е. из нескольких договоров игрок согласился на явно не выгодный для себя договор, то можно заподозрить что этот игрок кому-то подыгрывает." - А почему не выгодный для себя договор, если через несколько шагов этот участник выигрывает ( вместе ещё с двумя другими). Договор будет явно выгодный!

21.08.2022, 8:39 Усов Геннадий Григорьевич Отзыв: " И тут Остапа понесло ..." - Вы не читали "Двенадцать стульев"? Кажется, что из этой книги: "Вы как будто не представляете, как может проходить подобный чемпионат. Участников явно не четыре. А десятки, а может и сотни, из разных стран. Как там кто договорится?"

21.08.2022, 8:47 Усов Геннадий Григорьевич Отзыв: "Вы как будто не представляете, как может проходить подобный чемпионат. Участников явно не четыре. А десятки, а может и сотни, из разных стран. Как там кто договорится? "- А вот здесь Вы аккуратно пропускаете МАЛЕНЬКУЮ деталь. Чтобы победить среди 4-х участников (в группе товарищей), надо набрать 199 очков, против 99. И требуется 3 соучастника, чтобы "сдержать" одного. Чтобы победить среди большего числа участников, надо набрать 1999 очков против 199. А теперь определите МАТЕМАТИЧЕСКИ: сколько соучастников должны сдерживать одного участника, у которого 199 очков?

21.08.2022, 9:10 Усов Геннадий Григорьевич Отзыв: " Компьютерных игроков устроят только выгодные договоры. Каждый компьютер будет играть только для того, чтобы он сам получил максимальное количество очков." А зачем нужен игрок, если компьютер решает: с кем договариваться? И ещё: Вы путаете выгоду и количество очков. Есть очки, которые игрок "зарабатывает", а есть очки, которые "дарят за участие". Так Вы здесь разберитесь.

22.08.2022, 2:04 Харт Алекс Отзыв: «А почему не выгодный для себя договор, если через несколько шагов этот участник выигрывает ( вместе ещё с двумя другими). Договор будет явно выгодный!» - Вы снова не догоняете. Два договора предлагается. 1-ый. Двум сильным королям поделить победу пополам, каждому по 200 очков. 2-ой. Три короля договариваются по 133 очка. Какой выигрыш больше: 133 или 200? Если уж на то пошло, то можно считать, что в игре выигрывают всегда все игроки. Только кто-то может получить 0 очков, кто-то 100, кто-то 200, и т.д. Важно набрать как можно больше очков за игру. Я уже много раз Вам про это писал.

22.08.2022, 2:05 Харт Алекс Отзыв: «И тут Остапа понесло ..." - Вы не читали "Двенадцать стульев"?» - Остап говорил всегда что-то, чтобы одурманивать людей, а я наоборот пишу, чтобы не очень догоняющих людей чуть-чуть образумить.

22.08.2022, 2:06 Харт Алекс Отзыв: «А зачем нужен игрок, если компьютер решает: с кем договариваться?» - Приехали. Компьютерный игрок решает только за себя. А Вы за себя. Если между им и Вами будет консенсус, то договор может быть заключен. «И ещё: Вы путаете выгоду и количество очков. Есть очки, которые игрок "зарабатывает", а есть очки, которые "дарят за участие". Так Вы здесь разберитесь.» - Простите, я писал только об игроках, которые очки зарабатывают, каждый для себя. Про "дарят за участие" я ничего не писал.

22.08.2022, 2:16 Харт Алекс Отзыв: «А вот здесь Вы аккуратно пропускаете МАЛЕНЬКУЮ деталь.» - А вот здесь Вы снова не догоняете. «Чтобы победить среди 4-х участников (в группе товарищей), надо набрать 199 очков, против 99. И требуется 3 соучастника, чтобы "сдержать" одного.» - Во-первых, не всегда так. Если три игрока договорятся, то вероятность их выигрыша высока, но не равна 100%. Посмотрите на рис. 2. Видите короля крестей? На следующем ходу он предположим наберет 99 очков и трое других королей объединятся против него. И в обсуждаемом нами сценарии нужен король, имеющий тоже 99 очков, который будет сдерживать короля крестей. И нужен король, который наберет 199 очков. И сколько у нас останется: 400 – 99 – 99 – 199 = 3. 3 очка. А теперь посмотрите на рис. 2, правый нижний угол. Видите, эта карта блокируется королем крестей? А что если эта карта по достоинству выше, чем 3 очка? Поэтому если Вы хотите заранее договариваться, то лучше уж договариваться сразу четырем королям. Тогда вероятность победы будет равна 100%. «Чтобы победить среди большего числа участников, надо набрать 1999 очков против 199. А теперь определите МАТЕМАТИЧЕСКИ: сколько соучастников должны сдерживать одного участника, у которого 199 очков?» - (Ну чтобы победить число 199 достаточно иметь число 299, но не суть.) Давайте сначала вернемся к моему примеру с футболом, который вы продинамили. По сути, в футболе действует изначальная официальная договоренность. Точнее две. Первый договор 11-ти игроков, и второй договор 11-ти игроков. Это официальная договоренность. Но я писал про тайную договоренность перед началом игры. Я писал про 5 игроков, которые подыгрывают команде противника. И я задам Вам аналогичный вопрос, который Вы задали мне. Сколько игроков из 22 в футболе должны тайно договориться, чтобы у остальных не было шансов выиграть? У 10-ти есть шанс выиграть у 12-ти? У 5-ти есть шанс выиграть у 17-ти? У 1-го есть шанс выиграть у 21-го? Если этот один игрок, против которого договорились 21 игрок, это Электроник, то он сможет победить их. Смотрели фильм «Приключения Электроника»? Если он будет двигаться со скоростью 300 км/ч, то он легко сможет обыграть даже 21-го игрока в одиночку. Получается, чтобы победа была стопроцентной, то надо, чтобы все 22 игрока заранее договорились. Собственно я выше Вам про это и написал. Чтобы в игре из 4-ех игроков победа была стопроцентной нужен предварительный договор всех 4-ех участников. Аналогично и с игрой с большим количеством участников. Для стопроцентной победы нужен договор всех участников. Я надеюсь, Вы наконец поняли, что тайные договоренности могут быть в любой игре, и это нисколько не умаляет саму игру?

24.08.2022, 9:01 Усов Геннадий Григорьевич Отзыв: "А теперь определите МАТЕМАТИЧЕСКИ: сколько соучастников должны сдерживать одного участника, у которого 199 очков?» - (Ну чтобы победить число 199 достаточно иметь число 299, но не суть.)" - А вот теперь Вы уходите от вопроса: сколько соучастников должны сдерживать одного участника, у которого 199 очков?

24.08.2022, 9:11 Усов Геннадий Григорьевич Отзыв: "Я надеюсь, Вы наконец поняли, что тайные договоренности могут быть в любой игре, и это нисколько не умаляет саму игру?" и " Вы снова не догоняете. Два договора предлагается. 1-ый. Двум сильным королям поделить победу пополам, каждому по 200 очков. 2-ой. Три короля договариваются по 133 очка. Какой выигрыш больше: 133 или 200? Если уж на то пошло, то можно считать, что в игре выигрывают всегда все игроки." - Вы пытаетесь скрыться за цифрами: 133, 200. А если вы эти цифры сложите по участникам официального "договорняка", то получите 400. То есть, БАНК. Группа участников "берёт" банк (а 4-й - НИЧЕГО НЕ ПОЛУЧАЕТ). Таким образом, Вы предлагаете игру, в которой "группа товарищей" берёт банк. И лучше всегда иметь БАНК (в группе товарищей), чем быть 4-м (не знает о группе, но догадывается). А если догадываешься, то зачем садиться играть! Так кому нужна такая игра? Группе ...

24.08.2022, 9:49 Усов Геннадий Григорьевич Отзыв: Кстати, насчёт 199: как игрок после 99 очков наберёт 199 очков, если вокруг "рыскают" игроки с 99 очками? Объясните "мировому сообществу".

24.08.2022, 10:49 Харт Алекс Отзыв: «А вот теперь Вы уходите от вопроса: сколько соучастников должны сдерживать одного участника, у которого 199 очков?» - Я же Вам уже ответил. Если под словом «сдерживать» Вы понимаете итог игры, где он наберет официально 0 очков, то для 100-ной реализации такой задумки нужна договоренность всех игроков, включая его самого. Вы не видели, как я Вам ответил про сдерживание 3-мя игроками 4-го? Или Вы принципиально не видите то, что для Вас неудобно? Или Вы другой смысл вкладываете в слово «сдерживать»?

24.08.2022, 10:50 Харт Алекс Отзыв: «Вы пытаетесь скрыться за цифрами: 133, 200. А если вы эти цифры сложите по участникам официального "договорняка", то получите 400. То есть, БАНК. Группа участников "берёт" банк (а 4-й - НИЧЕГО НЕ ПОЛУЧАЕТ).» - Вы даете. Во-первых, я Вам ответил, что даже если 3-и игрока договорятся против 4-го, то нет 100%-ной вероятности, что они получат банк, а 4-ый ничего. Вы продинамили это? И снова пишете про 3-ех и 4-го. «Таким образом, Вы предлагаете игру, в которой "группа товарищей" берёт банк. И лучше всегда иметь БАНК (в группе товарищей), чем быть 4-м (не знает о группе, но догадывается).» - Кстати, расскажите, как будет формироваться эта группа товарищей? Допустим в одной игре Вы в группе товарищей, а в другой группа товарищей против Вас. Это на досуге подумайте. «А если догадываешься, то зачем садиться играть! Так кому нужна такая игра? Группе ...» - Вы даете. Я же Вам уже много раз писал, что если так рассуждать, то это в любой игре так. И зачем нужны все эти игры, если есть тайные договоренности, по которым распределяется банк? Я Вам уже приводил пример из шахмат и футбола. Придется Вам повторять, повторять и еще раз повторять, чтобы поняли. Повторяю еще раз. В футболе действует изначальная договоренность 11 на 11. Но можно тайно договориться с игроками противника и получить весь банк как Вы выражаетесь. А потом поделиться. Матч. На кону 1 млн. рублей. Если играть 11 на 11, то вероятность победы 50%. Вот одна из команд завербовала 4-х игроков противоположной команды, чтобы те ей подыгрывали. В итоге получается, что играют 15 игроков против 7 по факту. Но никто даже не догадывается. В итоге команда «11+4» побеждает команду «11-4» и банк, т.е. 1 млн. рублей делят на 15 человек. А те 7 даже не в курсе этого, и не понимают, как проиграла их команда. Думают, что просто не повезло, или плохо играли. И кому нужна игра футбол тогда? Вам так трудно понять этот пример? Или Вы принципиально его динамите, потому что он не удобен для Вас?

24.08.2022, 10:52 Харт Алекс Отзыв: «Кстати, насчёт 199: как игрок после 99 очков наберёт 199 очков, если вокруг "рыскают" игроки с 99 очками?» - Как вариант, может быть заключен договор между двумя игроками, у которых 99 очков. «Объясните "мировому сообществу".» - Мировое сообщество мне кажется уже давно все понимает. А вот у Вас с этим проблемы.

24.08.2022, 11:24 Усов Геннадий Григорьевич Отзыв: Подвожу итог своим рассуждениям. Далее вести полемику нет смысла. Главное: Вы в игре РАЗРЕШАЕТЕ ОФИЦИАЛЬНО (по правилам "игры") устраивать в процессе игры договорённости об игре "группы товарищей" против одного игрока. Об этом должно быть известно ДО НАЧАЛА ИГРЫ! И здесь меня не переубедить.

24.08.2022, 11:27 Усов Геннадий Григорьевич Отзыв: И подводя итог: в статье нет математики, а есть способ подсчёта очков, обязательный для каждого вида спорта!

24.08.2022, 12:00 Харт Алекс Отзыв: «Подвожу итог своим рассуждениям. Далее вести полемику нет смысла.» - Естественно нет смысла. Я же Вас «прижал» и Вам ответить по существу нечего. «Главное: Вы в игре РАЗРЕШАЕТЕ ОФИЦИАЛЬНО (по правилам "игры") устраивать в процессе игры договорённости об игре "группы товарищей" против одного игрока.» - ОФИЦИАЛЬНО разрешены выгодные договоры. Сколько раз Вам объяснять, что договор всех против одного более чем невыгоден? Когда могут победить двое, то зачем включать в договор третьего и потом с ним делиться очками? Я же Вам написал про игру с компьютерами на чемпионате. Если Вы компьютерам будете предлагать «давайте все против того одного компьютера», то эти компьютеры мягко говоря откажут Вам, потому что этот договор не будет им выгоден. Да, договоры разрешены. Но имеет смысл договариваться только по необходимости, с минимальным количеством игроков. Если два игрока могут договориться и победить, то зачем в долю брать третьего, четвертого? «Об этом должно быть известно ДО НАЧАЛА ИГРЫ!» - ДО НАЧАЛА ИГРЫ известно, что могут заключаться выгодные договора. И до начала игры всем известно кроме Вас, что не выгодно объединяться абсолютно всем против одного. «И здесь меня не переубедить.» - Естественно. Потому что все видят, что я Вас «прижал». Тут у Вас патовая ситуация. Вам проще упереться и все. У Вас нет аргументов.

24.08.2022, 12:04 Харт Алекс Отзыв: «И подводя итог: в статье нет математики, а есть способ подсчёта очков, обязательный для каждого вида спорта!» - И здесь все видят, что я Вас «прижал». Я ответил Вам на это и привел примеры. А у Вас как всегда аргументов нет. Есть новое понятие в математике, есть новая игра в математике, есть применение этого нового понятия в новой игре. А у Вас есть только один аргумент: «здесь нет математики и точка». Отличный аргумент. Возвращаясь к моему давнишнему совету. Вам следует самому поиграть в эту игру, чтобы лично убедиться в неверности своих тезисов. А сейчас получается, что Вы не играли в игру и пишете то, о чем не понимаете. Естественно садитесь в лужу. И Вам приходится все неудобные моменты динамить.

Оставить комментарий