- » Антропология
- » Археология
- » Архитектура
- » Астрономия
- » Библиотековедение
- » Биология
- » Биотехнологии
- » Ботаника
- » Ветеринария
- » Военные науки
- » География
- » Геология
- » Журналистика
- » За горизонтом современной науки
- » Зоология
- » Информационные технологии
- » Искусствоведение
- » История
- » Культурология
- » Лингвистика
- » Литература
- » Маркетинг
- » Математика
- » Машиностроение
- » Медицина
- » Менеджмент
- » Методика преподавания
- » Музыковедение
- » Нанотехнологии
- » Науки о Земле
- » Образование
- » Оптика
- » Педагогика
- » Политология
- » Правоведение
- » Психология
- » Регионоведение
- » Религиоведение
- » Сельское хозяйство
- » Социология
- » Спорт
- » Строительство
- » Телекоммуникации
- » Техника
- » Туризм
- » Управление и организация
- » Управление инновациями
- » Фармацевтика
- » Физика
- » Физическая культура
- » Филология
- » Философия
- » Химия
- » Экология
- » Экономика
- » Электроника
- » Электротехника
- » Юриспруденция
МОДАЛЬНОЕ УПРАВЛЕНИЕ АДАПТИВНОЙ ОПТИЧЕСКОЙ СИСТЕМОЙ, ОСНОВАННОЕ НА АНАЛИЗЕ НИЗКОЧАСТОТНОГО ПРОСТРАНСВЕННОГО СПЕКТРА ИЗОБРАЖЕНИЯ
СОЗДАНИЕ ФОТОПРИЕМНИКОВ СОЛНЕЧНОГО УФ ИЗЛУЧЕНИЯ ДЛЯ ЭКОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
РАСЧЕТ ДЕТОНАЦИОННЫХ ХАРАКТЕРИСТИК ЭНЕРГЕТИЧЕСКОГО КОМПОЗИЦИОННОГО СОСТАВА НА ОСНОВЕ ВЗРЫВЧАТОГО ВЕЩЕСТВА TKX-50 И ПОЛИМЕРНОГО СВЯЗУЮЩЕГО HTPB
АНАЛИЗ УРАВНЕНИЯ СОСТОЯНИЯ ПРОДУКТОВ ДЕТОНАЦИИ TKX-50, ПОЛУЧЕННОГО В ТЕРМОХИМИЧЕСКОМ РАСЧЕТЕ
Разделы: Физика
Размещена 02.01.2023.
Просмотров - 450
К ВОПРОСУ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ИНТЕНСИФИЦИРОВАННОГО ТЕПЛООБМЕНА В ОБЛАСТЯХ ПРИСОЕДИНЕНИЯ ПОТОКА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ТРУБАХ С ТУРБУЛИЗАТОРАМИ НА ОСНОВЕ УРАВНЕНИЯ БАЛАНСА ТУРБУЛЕНТНОЙ ПУЛЬСАЦИОННОЙ ЭНЕРГИИ И ДВУСЛОЙНОЙ МОДЕЛИ ПОТОКА
Лобанов Игорь Евгеньевичдоктор технических наук
Московский авиационный институт
ведущий научный сотрудник
УДК 532.517.4 : 536.24
1. ВВЕДЕНИЕ
Моделирование интенсифицированного теплообмена при турбулентном течении в каналах с турбулизаторами для открытых впадин и относительно малых высот турбулизаторов очень важно, поскольку именно в этой области имеет место высокий уровень интенсификации теплообмена при относительно незначительном повышении гидравлического сопротивления [1]. В этом случае имеет место отрыв и присоединение потока.
Ранее данный подход применялся для решения задачи о предельном теплообмене при турбулентном течении в каналах за счет турбулизации потока [2, 3].
Ранее в смысле генерирования обобщённой теории рассматривались турбулизаторы потока, высота которых меньше или равна толщине пристенного слоя [9—13]. В этом случае возмущения, сгенерированные турбулизаторами, в ядре потока невелики, следовательно, остается справедливой формула для пути смешения l = æ · y ( y — поперечная координата; æ — константа для пути смешения) и логарифмический профиль скорости [4].
В рамках настоящего научного исследования рассматриваются аспекты теории интенсифицированного теплообмена, которая была бы применима и к турбулизаторам бóльших высот, в том числе, больше пристенного слоя.
2. ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ ИНТЕНСИФИЦИРОВАННОГО ТЕПЛООБМЕНА В ОБЛАСТЯХ ПРИСОЕДИНЕНИЯ ПОТОКА ПРИ ПРИМЕНЕНИИ УРАВНЕНИЯ БАЛАНСА ТУРБУЛЕНТНОЙ ПУЛЬСАЦИОННОЙ ЭНЕРГИИ
В областях присоединения потока довольно успешно использовался метод расчёта теплообмена, основанный на решении уравнения баланса пульсационной турбулентной энергии [9—13]. Следует сказать, что методы, реализованные в работах [9—13], имели определённые ограничения, поэтому необходимо разработать такую теорию на основе баланса турбулентной энергии, которая имела бы более широкую общность, чем [9—13].
Необходимость генерирования теории для расчёта теплообмена, основанной на уравнении баланса турбулентной энергии, обусловливается тем, что аналогия Рейнольдса, на базе которой основан расчёт теплообмена при турбулентном течении в трубах, строго говоря, не может быть непосредственно использована для расчёта теплообмена в трубах с дискретными турбулизаторами потока, в том числе, в трубах с диафрагмами, поскольку в критических точках — в областях отрыва и присоединения потока — она нарушается, но справедлива вне вышеуказанных областей.
Для решения задачи о теплообмене в областях присоединения потока с привлечением уравнения баланса турбулентной пульсационной энергии, необходимо сгенерировать расчётную схему потока.
Схема течения в трубах с турбулизаторами представляется следующим образом. Поток на расстоянии от 5 до 8 высот турбулизатора отрывается от турбулизатора высотой h и снова присоединяется к гладкой поверхности трубы, образуя область присоединения. В вышеупомянутой области присоединения имеют место сильные пульсации, поэтому к ней можно описать критической точкой, т.е. точкой, где касательные напряжения τw=0, а плотность теплового потока максимальна qw=qwmax.
При отрывном обтекании напряжение трения равно нулю, но турбулентность потока велика и турбулентная энергия диффундирует к стенке, что и обусловливает, в том числе, интенсификацию теплообмена в области присоединения. Экспериментальные данные по измерению напряжения трения на стенке указывают на то, что в областях присоединения потока τw≈0 при очень незначительном разбросе экспериментальных точек [7, 8, 21].
В критических точках происходит полное нарушение аналогии Рейнольдса, обусловливая то, что эти точки являются идеальными с точки зрения интенсификации теплообмена, обеспечивая в них стремление к нулю значения фактора аналогии Рейнольдса r : r:=ξ/St→0, где St — число Стентона, ξ — коэффициент сопротивления.
В процессе генерирования критических точек имеет место необходимость затраты определённой энергии. Известный эффект превалирующего увеличения теплообмена над увеличением гидравлического сопротивления [1] при относительно малых высотах турбулизаторов можно объяснить положительным влиянием областей отрыва и присоединения потока, в то время как потери энергии, связанные с отрывом потока при относительно малых высотах турбулизаторов довольно незначительны, а при увеличении высоты турбулизаторов эта энергия возрастает и превалирования теплообмена над гидросопротивлением не возникает.
Вышесказанное обусловливает важность рассмотрения вопроса о теплообмене в критических точках для детерминирования интенсифицированного теплообмена в трубах с турбулизаторами.
Как уже отмечалось, в рамках настоящего научного исследования рассматриваются аспекты теории теплообмена в критических точках, которая была бы применима и к турбулизаторам как малых, так и больших высот, в том числе, больше пристенного слоя; в последнем случае высота турбулизаторов будет больше расстояния от стенки трубы до нижней границы турбулентного ядра потока (области логарифмического профиля скорости), а возмущения от турбулизаторов будут интенсивно распространяться на всю толщину пограничного слоя.
Уравнения баланса турбулентной пульсационной энергии для рассматриваемого случая будет иметь следующий вид [14, 15]:
 (1)
(1)
где ![]() — кинетическая энергия турбулентного пульсационного движения;
— кинетическая энергия турбулентного пульсационного движения; ![]() — компоненты пульсационной составляющей скорости; a и b — константы диссипации и диффузии соответственно.
— компоненты пульсационной составляющей скорости; a и b — константы диссипации и диффузии соответственно.
Рассматривается несжимаемая жидкость с постоянными физическими свойствами. Для несжимаемой жидкости с постоянными теплофизическими свойствами турбулентная кинематическая вязкость определяется как:![]() . (2)
. (2)
На основе анализа теории размерностей имеем:
![]() . (3)
. (3)
В отрывных зонах распределение τ аппроксимируется независимо от характера его изменения поперёк турбулентного пограничного слоя следующим образом [16]:
![]() (4)
(4)
где m — константа.
При y=0 — τ=0, что и определяет отрыв потока.
Подставив в (1) выражения (2)—(4), получим дифференциальное уравнение для кинетической энергии турбулентного пульсационного движения в следующем виде: . (5)
. (5)
Дифференциальное уравнение относительно кинетической энергии пульсационного движения будет выглядеть следующим образом:
 . (6)
. (6)
Последнее дифференциальное уравнение является нелинейным, поэтому представляется оптимальным в области присоединения потока (а также в области присоединённого пограничного слоя, лежащего от собственно области присоединения до полностью развитого течения) принять линейный характер изменения кинетической энергии пульсационного движения:![]() . (7)
. (7)
Подставив (7) в (6), получим следующее уравнение:
 , (8)
, (8)
решив которое, получаем:
![]() . (9)
. (9)
Отрицательный корень не удовлетворяет физическим условиям, поэтому он должен быть отброшен, следовательно:
![]() . (10)
. (10)
В данном исследовании рассматривается двуслойная схема турбулентного потока: турбулентное ядро потока и область непосредственного влияния вязкости.
На границе вязкого подслоя y=y0, а на границе турбулентного ядра — y=y1; соответственно: k при y=y0 равно k0 и k при y=y1 равно k1.
Внешняя граница турбулентного ядра y1 является таким расстоянием от стенки, где нарушается линейное распределение поперёк пристенного слоя кинетической энергии пульсационного движения k.
В районе области присоединения потока уровень турбулентной кинетической энергии k вблизи стенки является повышенным, что обусловливает и повышенный уровень турбулентной кинематической вязкости νТ .
Значение величины y0 является такое значение y, при котором величина относительной турбулентной вязкости νТ /ν становится такой же, как и в гладкой трубе на границе турбулентного и промежуточных областей. Т.к. уровень турбулентности в трубах с турбулизаторами выше, чем в гладких трубах, то абсолютная величина y0 в трубах с турбулизаторами будет меньше, чем в гладких трубах.
При φ=40 для гладкой трубы — νТ /ν=16.
В соответствии с (9) или (7) получим:![]() . (11)
. (11)
Подставив в (11) выражения для νТ =y·c∙k1/2 и νТ /ν=16, получим: . (12)
. (12)
Далее определим значение комплекса ![]() в зависимости от числа Рейнольдса
в зависимости от числа Рейнольдса ![]() (D — диаметр трубы;
(D — диаметр трубы; ![]() — среднерасходная скорость):
— среднерасходная скорость):
 . (13)
. (13)
Число Стентона, отнесённое к среднему температурному напору, детерминируем на основании известного соотношения, используемого для расчёта интенсифицированного теплообмена [2; 3; 7—13; 17, 21]:
 , (14)
, (14)
где Pr — число Прандтля; PrT — турбулентное число Прандтля; ν — кинематическая вязкость; νТ — турбулентная кинематическая вязкость; выражение в квадратных скобках — отношение максимального температурного напора к среднему, которое ранее было детерминировано в работах [11—13; 17].
Точные аналитические решения для интегралов, входящих в отношение максимального температурного напора к среднему  (r=R/R0 — безразмерный (или относительный) радиус трубы), входящего в решение задачи об интенсифицированном теплообмене в прямых круглых трубах с турбулизаторами при турбулентном течении при использовании обозначений —
(r=R/R0 — безразмерный (или относительный) радиус трубы), входящего в решение задачи об интенсифицированном теплообмене в прямых круглых трубах с турбулизаторами при турбулентном течении при использовании обозначений —  — выглядят следующим образом:
— выглядят следующим образом:
 (15)
(15) (16)
(16) (17)
(17)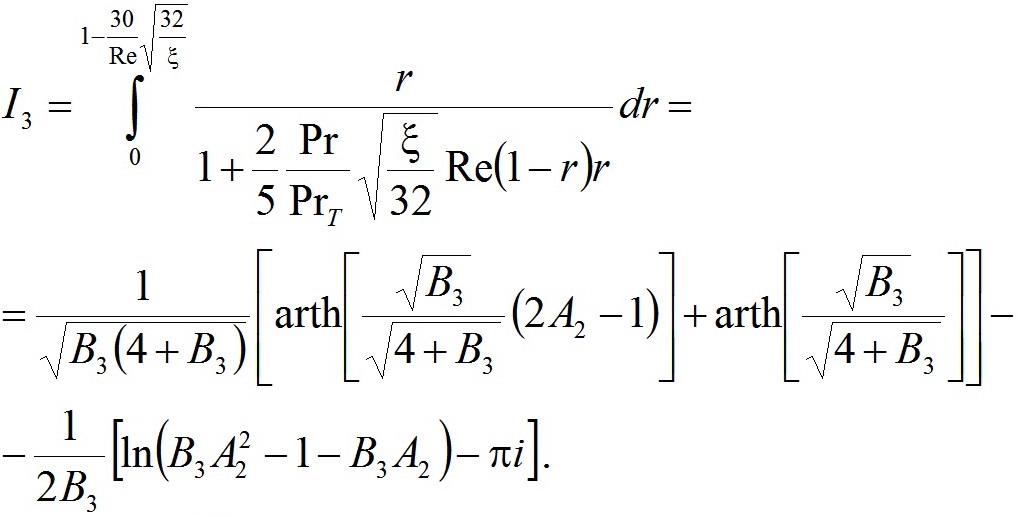 (18)
(18) (19)
(19) (20)
(20) (21)
(21)
Окончательное выражение для числа Стентона получим путём подстановки значения ![]() из (13) в (14):
из (13) в (14): . (22)
. (22)
В данном исследовании используем двуслойную схему потока, поэтому интеграл, входящий в (22), можно записать следующим образом:
 . (23)
. (23)
Величина толщины вязкого подслоя в сечении отрыва турбулентного пограничного слоя принимается стандартной ηВ=5 (η=yw*/ν — безразмерная координата; w* — скорость трения).
В вязком подслое и в промежуточной области, т.е. при у > y0, распределение величины νТ /ν происходит так же, как и в гладкой трубе, по закону "четвёртой степени" убывания турбулентной вязкости с расстоянием, а именно:
![]() , (24)
, (24)
для промежуточного подслоя:
![]() , (25)
, (25)
для турбулентного ядра потока:
![]() . (26)
. (26)
В сечении отрыва турбулентного пограничного слоя безразмерная толщина вязкого подслоя, как показано в работе [18], равна: . (27)
. (27)
Иными словами, ηВ≈7,55. Данное значение, полученное в [18], является ощутимо завышенным, поскольку она была детерминирована в [18] без учёта буферной (промежуточной) области, что подтверждает правильность принятия стандартной величины вязкого подслоя в сечении отрыва турбулентного пограничного слоя.
Теперь необходимо детерминировать величины, входящие в окончательное выражение для числа Стентона (23).
Сопоставление турбулентной вязкости из выражения (3) с турбулентной вязкостью, детерминированной путём вычисления на основании обычного логарифмического профиля скорости для области постоянного напряжения позволяет получить постоянную с:
 , (28)
, (28)
поэтому
![]() , (29)
, (29)
что соответствует значению, принятому в [2; 3; 7—13, 21].
Распределение величины турбулентной пульсационной кинетической энергии k, экспериментально детерминированное в [19], указывает на то, что линейность распределения величины k нарушается в районе порядка внешней границы области постоянного напряжения:
![]() . (30)
. (30)
Следовательно,
![]() . (31)
. (31)
Для расчёта интенсифицированного теплообмена в точке присоединения принимаем y1/y0=12.
Ввиду неопределённости в области присоединения пограничного слоя значения w* (в точке отрыва w*=0), то абсолютное значение y1 бессмысленно детерминировать из полученного ранее условия y1/ y0.
Исходя из данных, приведённых в [19], область постоянного напряжения заканчивается на расстоянии, равном 1/5¸1/10 толщины пограничного слоя, поэтому для прямой круглой трубы величину y1 можно оценить как:
![]() . (32)
. (32)
Вышеуказанное значение y1/D полностью коррелирует с соответствующей рекомендацией, приведённой в [15] на основании анализа экспериментальных данных.
Для детерминирования значения y0/D следует воспользоваться соотношением относительно величин, которые были определены выше:
![]() . (33)
. (33)
Далее необходимо детерминировать интегралы, входящие в (23), как для вязкого подслоя, так и для турбулентного ядра потока.
Для вязкого подслоя вышеуказанный интеграл будет равен:
 . (34)
. (34)
После проведения интегрирования, получим:
 . (35)
. (35)
Возможно и альтернативное эквивалентное решение для интеграла (34), основанное на использовании гипергеометрической функции (функции Гаусса):
 , (36)
, (36)
где ![]() — гипергеометрическая функция.
— гипергеометрическая функция.
Для турбулентного ядра вышеуказанный интеграл будет равен: . (37)
. (37)
Введя следующие обозначения:![]() , (38)
, (38)
приведём, после интегрирования, следующую форму записи интеграла (37):
 (39)
(39)
Таким образом, расчёт интенсифицированного теплообмена в точке присоединения в трубах с турбулизаторами может быть проведён по формуле (23) с расчётом входящих в неё интегралов по формулам (35) (или (36)) и (39).
Сравнение теоретических расчётных данных по теплообмену в точке присоединения турбулентного пограничного слоя с экспериментальными удобнее сделать так же, как это сделано в работах [7, 8, 21]. Сходные условия теплообмена имеют место для теплообмена в задней критической точке при поперечном обтекании цилиндра [7, 8, 20, 21]:
 , (40)
, (40)
где ![]() — скорость набегающего потока; DЦ — диаметр цилиндра.
— скорость набегающего потока; DЦ — диаметр цилиндра.
Значения ![]() и
и ![]() на границах вязкого подслоя и турбулентного ядра соответственно детерминируется так же, как и в работах [2, 3, 7—13, 17, 21], поскольку вышеуказанные зависимости имеют широкую общность:
на границах вязкого подслоя и турбулентного ядра соответственно детерминируется так же, как и в работах [2, 3, 7—13, 17, 21], поскольку вышеуказанные зависимости имеют широкую общность:
 , (41)
, (41)
где R=D/2 — радиус трубы (h/R=1–d/D, d — диаметр диафрагмы), Re — число Рейнольдса, ξ — коэффициент сопротивления трению.
В работах [7, 8, 21] приводится формула по в области присоединения турбулентного пограничного слоя, основанная на обобщёнии экспериментальных данных для диапазона Re=104¸105:
![]() . (42)
. (42)
Использованная в данном исследовании закономерность является более обоснованной и сложной, чем использованная в [7, 8, 21], что обусловливает её преимущественное применение.
Сравнение сгенерированной теории с экспериментом [7, 8, 20, 21] оптимальнее всего провести для тех условий, для которых было проведено сравнение для других математических моделей [7, 8, 21] — для Re=104 и h/R=0,0632 — ![]() =0,34 [7, 8, 21] число Стентона составляет St=4,579·10–3, в то время как на основании эксперимента [7, 8, 20, 21] — StЭ=4,642·10–3; ошибка составляет порядка 1,5%, в то время как ошибка расчётной модели, представленной в [7, 8, 21], составила порядка 19% [7, 8, 21].
=0,34 [7, 8, 21] число Стентона составляет St=4,579·10–3, в то время как на основании эксперимента [7, 8, 20, 21] — StЭ=4,642·10–3; ошибка составляет порядка 1,5%, в то время как ошибка расчётной модели, представленной в [7, 8, 21], составила порядка 19% [7, 8, 21].
Следовательно, сгенерированная в данном научном исследовании теоретическая модель для расчёта интенсифицированного теплообмена в точке присоединения турбулентного пограничного слоя практически на порядок точнее существующей [7, 8, 21], однако полученные в работе окончательные расчётные зависимости гораздо сложнее существующих [7, 8, 21], что не важно при современном уровне развития вычислительной техники.
3. ЗАКЛЮЧЕНИЕ
В исследовании сгенерирована теоретическая модель на базе уравнения баланса турбулентной пульсационной энергии, позволяющая теоретическим образом детерминировать интенсифицированный теплообмен при турбулентном течении в каналах с турбулизаторами для большого диапазона высот турбулизаторов в области присоединении турбулентного пограничного слоя. Получена их удовлетворительная корреляция с существующими независимыми экспериментальными данными. Сгенерированная теория гораздо точнее, использует меньшее число допущений и лучше соответствует имеющемуся экспериментальному материалу, чем существующие теории [7, 8, 21].
Показано, что решение уравнения баланса турбулентной энергии для расчёта теплообмена в каналах со сложной гидрогазодинамикой, в том числе, в точке присоединения турбулентного пограничного слоя, является прогрессивным направлением в теории интенсифицированного конвективного теплообмена, поскольку оно позволяет получить надёжные расчетные методики в тех случаях, когда имеет место нарушение аналоги Рейнольдса.
Разработанная теория указывает на то, что необходима дальнейшая работа в направлении её развития и перехода от двуслойной модели потока к трёхслойной, которая позволит детерминировать теплообмен в точке присоединения турбулентного пограничного слоя в более широком диапазоне определяющих параметров и с большей точностью, чем для существующих моделей.
Решение теоретической задачи о теплообмене в области присоединения турбулентного пограничного слоя обусловливает потенциальное решение задачи о теплообмене и для всей области после присоединения турбулентного пограничного слоя (присоединённый пограничный слой): от точки присоединения турбулентного пограничного слоя вплоть до полностью развитого течения (до стабилизированного течения).
1. Эффективные поверхности теплообмена / Э.К.Калинин, Г.А.Дрейцер, И.З.Копп и др. — М.: Энергоатомиздат, 1998. — 408 с.
2. Лобанов И.Е. Моделирование предельного изотермического теплообмена при турбулентном течении в каналах за счет турбулизации потока на базе уравнения баланса турбулентной пульсационной энергии // Проблемы газодинамики и тепломассообмена в энергетических установках: Труды XV Школы-семинара молодых ученых и специалистов под руководством академика РАН А.И.Леонтьева. — М., МЭИ, 2005. — T.1. — С. 99—102.
3. Лобанов И.Е. Предельный теплообмен при турбулентном течении в каналах за счет турбулизации потока на базе уравнения баланса турбулентной пульсационной энергии // Труды Четвертой Российской национальной конференции по теплообмену. В 8 томах. Т. 2. . Вынужденная конвекция однофазной жидкости. — М., 2002. — С. 191—194.
4. Шлихтинг Г. Теория пограничного слоя. — М.: Наука, 1974. — 712 с.
5. Webb R.L., Eckept E.R. and Goldstein R.J. Heat Transfer and friction in tubes with Repeated—Rib Ronghness // Int. J. Heat Mass Transfer. — 1971. — Vol.14. — № 4. — P.601—617.
6. Кутателадзе С.С. Основы теории теплообмена. — М.: Атомиздат, 1979. — 416 с.
7. Мигай В.К. Повышение эффективности современных теплообменников. — Л.: Энергия. Ленинградское отделение, 1980. — 144 с.
8. Мигай В.К. Моделирование теплообменного энергетического оборудования. — Л.: Энергоатомиздат. Ленинградское отделение, 1987. — 263 с.
9. Лобанов И.Е., Мякочин А.С., Низовитин А.А. Моделирование интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами на базе уравнения баланса турбулентной пульсационной энергии // Вестник МАИ. — 2007. — Т. 14. — № 4. — С. 13—22.
10. Лобанов И.Е., Парамонов Н.В. Математическое моделирование теплообмена в трубах с турбулизаторами при турбулентном течении на основе уравнения баланса турбулентной пульсационной энергии // Труды Пятой Российской национальной конференции по теплообмену. В 8 томах. Том 2. Вынужденная конвекция однофазной жидкости. — М.: МЭИ, 2010. — С. 162—165.
11. Лобанов И.Е. Применение уравнения баланса турбулентной пульсационной энергии для математического моделирования интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами // Авиакосмическое приборостроение. — 2011. — № 5. — С. 19—24.
12. Лобанов И.Е. Теория интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами на базе уравнения баланса турбулентной пульсационной энергии // Материалы IX Международной конференции по неравновесным процессам в соплах и струях (NPNJ'2012), 25—31 мая 2012 г., Алушта. — М.: Издательство МАИ, 2012. — С. 245—247.
13. Лобанов И.Е. Теория интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами на основе уравнения баланса турбулентной пульсационной энергии // Отраслевые аспекты технических наук. — 2012. — № 5. — С. 7—14.
14. Praudte L. Über ein neues Formelsystem für die ausgebildete Turbulenz // Nachrichten der Akad. Wiss. — Göttingen: Mathphys, 1945. — P. 6.
15. Spolding D.B. Heat transfer for turblent separated flows // Journal Fluid Mechanics. — 1967. — Vol. 27. — Part 1. — P. 97—109.
16. Гинзбург И.П. Теория сопротивления и теплопередачи. — Л.: ЛГУ, 1970. — 375 с.
17. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том IV. Специальные аспекты математического моделирования гидрогазодинамики, теплообмена, а также теплопередачи в теплообменных аппаратах с интенсифицированным теплообменом. – М.: МГАКХиС, 2011. – 343 с.
18. Кутателадзе С.С., Леонтьев А.И. Тепломассообмен и трение в турбулентном пограничном слое. — М.: Энергоатомиздат, 1985. — 320 с.
19. Таунсенд А. А. Структура турбулентного потока с поперечным сдвигом, Издательство иностранной литературы, 1959. — 399 с.
20. Richardson P.D. Heat and mass transfer in turbulent separated flows // Chem. Engng. Sc. — 1963. — Vol. 18. — P. 149.
21. Мигай В.К. К теории теплообмена в турбулентном потоке с отрывом // Известия АН СССР. Механика жидкости и газа. — 1976. — № 2. — С. 170—171.
Рецензии:
2.01.2023, 15:29 Ашрапов Улугбек Товфикович
Рецензия: Использование уравнения баланса Турбулентной энергии в дополнение к уравнениям Рейнольдса впервые было предложено Колмогоровым в 1942 г.[https://scask.ru/n_book_s_gidro.php?id=46]. В данной работе автором разработана теоретическая модель для расчёта теплообмена при турбулентном течении в каналах в условиях интенсификации теплообмена, отличающаяся от известных моделей более высокой точностью. Полученные расчётные данные по интенсифицированному теплообмену хорошо соответствуют существующими экспериментальными данными.Работа актуальная и может быть использована при разработке методов интенсификации теплообмена в твердотопливных котлах с тягой или микроканальных теплообменниках гибридных систем термостабилизации. Работу рекомендую к публикации в журнале sci-article.ru.
Комментарии пользователей:
Оставить комментарий
Вверх