- » Антропология
- » Археология
- » Архитектура
- » Астрономия
- » Библиотековедение
- » Биология
- » Биотехнологии
- » Ботаника
- » Ветеринария
- » Военные науки
- » География
- » Геология
- » Журналистика
- » За горизонтом современной науки
- » Зоология
- » Информационные технологии
- » Искусствоведение
- » История
- » Культурология
- » Лингвистика
- » Литература
- » Маркетинг
- » Математика
- » Машиностроение
- » Медицина
- » Менеджмент
- » Методика преподавания
- » Музыковедение
- » Нанотехнологии
- » Науки о Земле
- » Образование
- » Оптика
- » Педагогика
- » Политология
- » Правоведение
- » Психология
- » Регионоведение
- » Религиоведение
- » Сельское хозяйство
- » Социология
- » Спорт
- » Строительство
- » Телекоммуникации
- » Техника
- » Туризм
- » Управление и организация
- » Управление инновациями
- » Фармацевтика
- » Физика
- » Физическая культура
- » Филология
- » Философия
- » Химия
- » Экология
- » Экономика
- » Электроника
- » Электротехника
- » Юриспруденция
Разделы: Телекоммуникации, Техника
Размещена 24.09.2014. Последняя правка: 23.09.2014.
Просмотров - 4329
БЫСТРЫЙ АДАПТИВНЫЙ АЛГОРИТМ ПОДАВЛЕНИЯ КОМБИНИРОВАННЫХ ПОМЕХ С ИЗМЕНЯЮЩЕЙСЯ МОЩНОСТИ ШУМА
Нгуен Фат Тьенк.т.н
Вьетнамский государственный технический университет имени Ле Куй Дона
Преподаватель
к.т.н., доцент Нгуен Хy Хоанг (Вьетнамский государственный технический университет имени Ле Куй Дона); Научный руководитель: к.т.н., доцент Андреев Владимир Григорьевич (РГРТУ)
УДК 621.396
Введение. Для работы радиотехнических систем характерно воздействие комбинированных (комплексов коррелированных и некоррелированных) помех, которые, поступая на вход приемника вместе с полезными сигналами, затрудняют их обнаружение и обработку. Борьба с негативным влиянием таких мешающих процессов заключается в обелении коррелированной компоненты до уровня шумов Pn. В ряде практических приложений величина Pn подвержена быстрым изменениям во времени, а статистические свойства коррелированных помех остаются при этом неизменными [1,2]. Оптимальное решение предполагает для оценки параметров обеляющего помехи фильтра пересчёт коэффициентов обратной корреляционной матрицы помех при изменении уровня мощности Pn шумовой составляющей. Известное упрощенное решение заключается в сохранении прежних значений вектора обработки, что характерно, например, для режекторных фильтров [3]. Отметим, что оптимальное решение сопряжено со значительными вычислительными затратами, а известное неадаптивное приводит к недоиспользованию потенциальных возможностей по обработке сигналов на фоне комбинированных помех.
Цель работы — сокращение вычислительных затрат при реализации адаптивного алгоритма подавления комбинированных помех в условиях изменения мощности Pn их некоррелированной компоненты.
Постановка задачи. Представим корреляционную матрицу R мешающего процесса как сумму коррелированной Rс и некоррелированной PnI компонент соответственно:
|
|
(1) |
где Rc — (q+1)×(q+1)‑мерная корреляционная матрица коррелированной компоненты мешающего процесса, q — порядок фильтра его подавления, I — (q+1)×(q+1)‑мерная единичная матрица, Pn — относительная мощность шумовой компоненты мешающего процесса.
Вычислительные затраты, которые требует процедура обращения матриц, пропорциональны кубу величины q, а в случае использования быстрых процедур обращения — квадрату q [4]. Предлагается найти поправочный двумерный вектор χT=[χ1; χ2] [4], домножение которого на известную диагональную матрицу diag(a) и на дополнительную эвристически найденную матрицу М приблизительно равно вектору aopt оптимальной обработки: diag(a)Мχ ≈ aopt или
|
diag(a)Мχ = aopt+e, |
(2) |
где e — вектор-столбец невязки, M — [(q+1)×2]‑мерная дополнительная матрица, имеющая вид:

Вектор aT=[a1;a2;…; aq] коэффициентов обеляющего нерекурсивного фильтра q‑го порядка при нормировке к единице нулевого коэффициента a0 импульсной характеристики можно представить в виде уравнения Юла-Уолкера [4]:
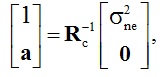 |
(3) |
где ![]() — дисперсия возбуждающего шума. Выражение (3) может быть представлено в виде:
— дисперсия возбуждающего шума. Выражение (3) может быть представлено в виде:
a=−Rc−1r,
где rT=[R1; R2; …; Rq] — автокорреляционная последовательность мешающего коррелированного процесса с единичной дисперсией R0=1, Rc — корреляционная матрица, аналогичная представленной в выражении (1), мерность которой сокращена до (q×q).
В условиях присутствия некоррелированной компоненты мешающего процесса оптимальное решение принимает вид: aopt= −(Rc+PnI)−1r [7].
Аналитическое решение. На основании выражения (2) имеется возможность выразить вектор e невязки между оптимальным и предлагаемым решениями:
e=(Rc+PnI) diag(a)Мχ+r.
Предлагается для нахождения двумерного корректирующего вектора χ использовать критерий минимума квадрата длины q‑мерного вектора e невязки, т.е. минимума среднеквадратической ошибки:
|
|
(4) |
где C2 — двумерное пространство комплексных чисел, * — знак комплексного сопряжения. Корректирующий вектор χ, при котором выполняется требование (4), соответствует оптимальному значению χopt корректирующего вектора.
Для нахождения минимума функции eT*e(χ) возьмем производную по вектору χ и приравняем её к двумерному нулевому вектору 0:
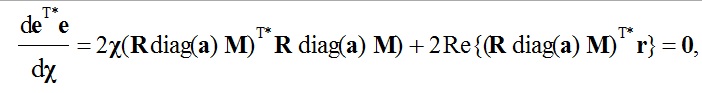 |
(5) |
где Re{•}— оператор выделения действительной части, 0 — нулевой двумерный вектор градиента целевой функции eT*e(χ). Полагая матрицу преобразований B=R diag(a) М, выражение (5) можно записать как решение системы нормальных уравнений:
| |
(6) |
Вычисление χopt в соответствии с (6) требует операцию обращения матрицы BT*B, которая имеет мерность (2×2). Обращение BT*B с точностью до константы (определителя) может быть произведено просто перестановкой элементов матрицы со сменой знака соответствующего алгебраического дополнения, т.е. сложной процедуры обращения не требуется.
Для подтверждения факта нахождения глобального минимума целевой функции eT*e(χ) в точке с координатами χopt проанализируем знак второй производной:
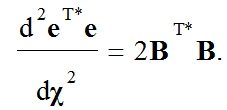 |
(7) |
Из выражения (7) видно, что (2×2)‑мерная квадратная матрица вторых производных представляет собой удвоенное произведение транспонированной и комплексно сопряжённой величины BT* на исходную матрицу B и поэтому определена положительно [4], что подтверждает оптимальность найденного по (6) решения.
Экспериментальные исследования. Практические исследования показали, что эффективность коррекции по критерию (4) квадрата длины вектора e невязки существенно зависит от порядка q фильтра. Это связано с тем, что с ростом q увеличивается число компонент ak вектора обработки a, подлежащих коррекции. Так, при втором порядке фильтра (q=2) diag̣̣̣̣̣̣̣̣̣̣̣(a)χ = aopt, т.к. корректирующий вектор тоже двумерен. В случае большего числа коэффициентов ak (q>2) точно скорректировать их все двумерным корректирующим векторным множителем χ в общем случае невозможно. Поэтому с ростом порядка q фильтра подавления качество коррекции его параметров ухудшается. Проанализируем эффективность предлагаемой методики адаптации фильтра подавления комбинированных помех при q>2.
Сравним вычислительные затраты на адаптацию при оптимальном и предлагаемом решениях. В таблице 1 приведены приближенные формулы для оценки вычислительных затрат.
Из анализа таблицы следует, что при порядке фильтра q=3 выигрыш в вычислительных затратах составляет 1,23 раз, при q=4 — 1,95 раз, а при q=5 — 2,84 раз.
Поскольку в ряде радиотехнических приложений используются критерий Неймана-Пирсона, который предполагает максимизацию вероятности D правильного обнаружения при заданной вероятности F ложной тревоги, то сравним характеристики обнаружения для систем, реализующих известное неадаптивное, оптимальное и предлагаемое решения. Для этого оценим среднюю по относительным частотам FT сигнала вероятность правильного обнаружения при вероятности Fa ложной тревоги Fa=10-6, порядке фильтра q=4, уровне мощности Pn шумовой мешающей компоненты Pn=10-1, относительной ширине спектра помехи ΔFT=0,1 и относительной ширине спектра сигнала ΔFsT=0,01 [3, 4]. На рисунке 1 представлены зависимости средней вероятности правильного обнаружения от отношения Q сигнал‑(помеха+шум) по мощности. Известное решение (пунктирная линия 1) в среднем проигрывает и оптимальному (сплошная тонкая кривая 2) и предлагаемому (сплошная жирная кривая 3).
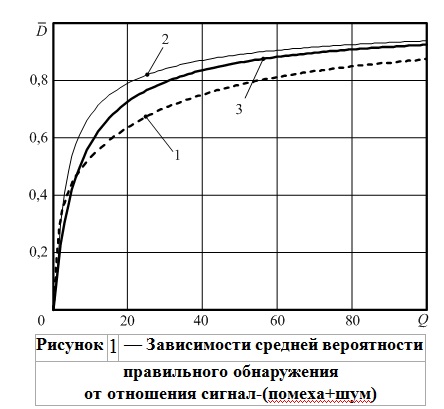
Так, при отношении сигнал‑(помеха+шум) Q=40 предлагаемое решение обеспечивает на 8 % большую среднюю вероятность правильного обнаружения, чем известное, уступая оптимальному на 3 %, а при Q=80 выигрыш перед известным решением составляет 6 %, а отличие от оптимального не превышает 1,5 %. При мощности Pn=10 некоррелированной компоненты характеристики обнаружения для оптимального и предлагаемого решений фактически совпадают, а выигрыш в средней вероятности правильного обнаружения перед известным решением при Q=40 составляет 28 %.
Выводы. Таким образом, анализ эффективности предлагаемого адаптивного алгоритма (4) расчёта коэффициентов обеляющего фильтра показал, что имеется выигрыш в 1,23…2,84 раз в вычислительных затрат по сравнению с оптимальным решением путем введения поправочный двумерный вектор χT=[χ1; χ2] при синтезе адаптивного обеляющего фильтра в условиях изменения мощности Pn некоррелированных помех. Анализ эффективности предлагаемого решения показал, что оно обладает выигрышами в средней вероятности правильного обнаружения на 6 %...28 % по сравнению с известным неадаптивным фильтром подавления комбинированных помех.
1. Андреев В.Г., Нгуен Т.Ф., Нарбеков А.Ю. Адаптивная фильтрация комбинированных помех // Вестник Рязанского государственного радиотехнического университета.— № 3.— Выпуск 45.— Рязань: РГРТУ, 2013.— C. 38 41.
2. Бакулев П.А. Радиолокационные системы: учебник для вузов.— М.: Радиотехника, 2004.— 320 c.
3. Бакулев П.А., Сосновский А.А. Радиолокационные и радионавигационные системы.— М.: Радио и связь, 1994.— 296 с.
4. Стренг Г. Линейная алгебра и её применения. — М.: Мир, 1980. — 454 с.
5. Кошелев В.И., Андреев В.Г. Синтез АРСС—моделей эхо-сигналов // Изв. вузов. Радиоэлектроника.— 1993.— Т.36.— №7.— C. 8 13.
6. Андреев В.Г. Оптимизация авторегрессионных моделей радиоотражений // Вестник Рязанского государственного радиотехнического университета.— № 1.— Выпуск 35.— Рязань: РГРТУ, 2011.— C. 12 15.
7. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ.– М.: Мир, 1990.– 584 с
Рецензии:
24.09.2014, 23:33 Клинков Георгий Тодоров
Рецензия: Статья рекомендуется к публикаций.Основания:
1.Практическая граница приложения на основе простого адаптивного алгоритма.
2.Алгоритм дает основания(в корелационном аспекте)принять схематичность данного опнимизирующего решения.
Спасибо вам!
Комментарии пользователей:
Оставить комментарий
Вверх
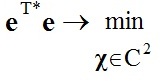 ,
,