Статья опубликована в №43 (март) 2017
Разделы: Физика
Размещена 08.03.2017. Последняя правка: 12.04.2017.
Просмотров - 1949

Системный метод прогнозирования новых физических величии (Продолжение)

Бессонов Евгений Александрович

Доктор технических наук

Горнодобывающие предприятия РФ

Консультант

УДК 006.915 (532.542)

Системный метод прогнозирования новых физических величин, как было ранее показано автором  в работах [1, 2, 3], заключается в разработке алгоритма прогнозируемой величины, – в составлении систематизированного набора отличающих ее признаков, а затем, на его основе и на результатах теоретических исследований, обозначенных в схеме (рис. 1), в создании новых пилотных (пробных) физических величин и их закономерностей.

В работах [1,2, 3] автором был представлен результат использования метода при исследовании  динамики твердого тела при нелинейном (криволинейном) движении,  выраженный в  получении ряда новых физических величин и их закономерностей.  В настоящей работе представлен результат, где аналогичному комплексному исследованию был подвержен другой раздел физики – гидродинамика, в которой еще остаются «белые пятна» в научном поле исследований.

 

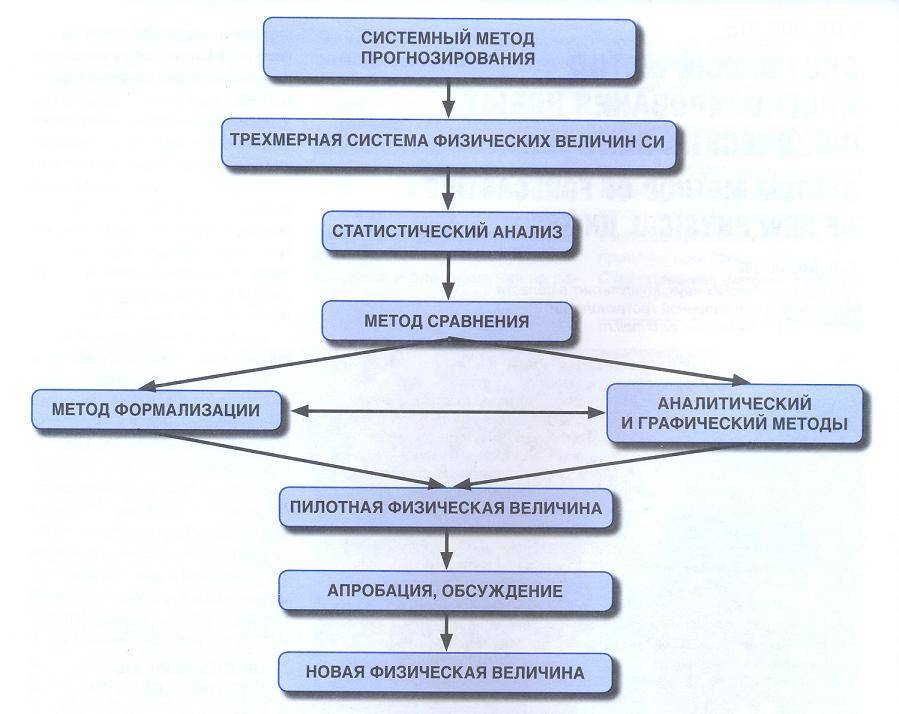
Рис.1. Схема поэтапного выполнения системного метода

Современная гидродинамика  изобилует множеством физических величин и закономерностей, объясняющих различные формы и процессы движения жидкости [6, 7]. Вместе с тем некоторые ее процессы до настоящего времени оставались недостаточно  изученными. Например, практически отсутствует научное объяснение переходных процессов ускоренного и замедленного течения вязкой  жидкости в закрытых системах с различной степенью сужения и расширения, т.е. нет научного обоснования таких процессов, отсутствуют их наименования, обозначения их величинами и описания формулами. Все это тормозит развитие теоретической и прикладной гидродинамики. Исследования в данной области знаний необходимы для изучения гидравлических закрытых систем с изменяемыми объемами пространства и геометрией потока жидкости.  Они также могут быть полезными в прикладной гидродинамике при разработке новых устройств (специальных насадок, форсунок,  конфузоров, диффузоров, всасывающих наконечников, выпусков и пр.) с заданными гидравлическими характеристиками.

Чтобы заполнить данный пробел в гидродинамике, автором, на основе предложенного системного метода, был проведен комплекс исследований, в результате которого были получены новые физические величины и установлены их закономерности.

Статистический анализ показал, что прогнозируемые величины исследуемых гидродинамических переходных процессов должны войти в I группу физических величин (механические и пространственно-временные величины) и относиться к подгруппам немассивных (М₂) и динамических поточных величин (Т8.1) [5]. В таблице логической системы СИ [8] данные физические величины I группы могут быть расположены только на пересечениях столбца № 22 (подгруппа по «массивности» М₂ – немассивные величины и подгруппа по «пространственности» L₄ – монометрические величины) и строк №№ 10b и 10с (подгруппы по «заряженности» I₁ – незаряженные величины и Т_8.1 – динамические поточные величины) в свободных ячейках таблицы.  Причем данные ячейки, в силу своего пространственного расположения в таблице [8], наделены следующими степенями: для канделы - J⁰; килограмма – М⁰; метра – L; для радиана – R⁰; ампера – I⁰; секунды– Т^-3; для стерадиана – S⁰; моли – N⁰; для кельвина – θ⁰. То есть прогнозируемые величины  в рассматриваемых и пока еще пустых ячейках таблицы будут иметь полную размерность  LM⁰T³I⁰J⁰θ⁰N⁰R⁰S⁰.

Метод сравнения показал, что в соответствии с классификацией [5] на строке № 10 расположен ряд физических величин, которые характеризуются «родственными» динамическими процессами: потоком энергии, плотностью потока энергии, скоростью нарастания давления, рывком (кинематическим) и др. Объединяющей единицей величин на строке № 10 по их «подвижности»  является секунда в минус третьей степени – Т^-3.   Поэтому все величины, лежащие на данной строке, включая искомые прогнозируемые  величины, будут относиться к динамическим поточным величинам и, согласно классификации [5],  обозначаться символом Т_8.1. Также объединяющей единицей величин в столбце № 22 по «пространственности»  является метр – L и согласно классификации [5] прогнозируемые величины будут относиться к монометрическому виду и обозначаться символом L₄. 

Обобщенная характеристика прогнозируемых пилотных величин в ячейках V-10-22 окончательно сведется к следующему алгоритму: по группам: величины будут принадлежать к I группе - к механическим и пространственно-временным величинам;  по подгруппам: по «массивности» будут относиться к виду М₂ – немассивные величины; по «подвижности» - к виду Т_8.1 – динамические поточные величины; по «пространственности» - к виду L₄ -  монометрические величины; по «заряженности» - к виду  I₁ – незаряженные величины;  по «температурности» -  к виду К₂ - нетемпературные величины; по «количественности» -  к виду N₂ - неколичественные величины; по «светоизлучательности» -  к виду J₂ - несветоизлучательные величины; по «радианности» -  к виду R₂ – нерадианные  величины; по «стерадианности» -  к виду S₂ – нестерадианные  величины.

В ячейках поля V-10-22 специализированной таблицы системы СИ [8] c размерностью  LM⁰T³I⁰J⁰θ⁰N⁰R⁰S⁰ расположена только одна известная величина  - рывок  J, которая применяется в кинематике (и электродинамике в IV группе величин) и в силу своей специфики не может быть использована в теории гидродинамики для научного описания процессов течения реальной жидкости. Поэтому необходимо было создать (спрогнозировать) новую физическую величину в этом разделе физики и выполнить ее научное обоснование.  Учитывая некоторую аналогию физических процессов и близкие по природе свойства, прогнозируемая величина в гидродинамике может получить наименование – гидродинамический рывок и обозначение  ‘J_h (знак штрих перед символом обозначает пилотность  величины). Данная величина может быть использована в теории гидродинамики при исследовании переходов равноускоренного течения вязкой жидкости из одного сужаемого пространства закрытой системы в другое, более сужаемое пространство системы. В обратном гидродинамическом процессе, т.е. при переходах равнозамедленного течения жидкости из одного расширяемого пространства закрытой системы в другое, более расширяемое пространство, напротив,  происходит снижение темпа его замедленного течения (стопорение), которое может быть названо гидродинамическим стопором и получить обозначение  ‘S_h.

Комплексный системный метод прогнозирования, помимо анализа, включает в себя и графические  исследования, которые позволяют наглядно продемонстрировать гидродинамические процессы изменения прогнозируемых величин и показать их графическое соотношение.

На рисунке 2 а, б показаны зависимости изменения скорости Uтекущей жидкости по длине l и времени (t) соответственно в сужающихся и расширяющихся каналах закрытых систем различной формы сечения. На основе изменений скоростей U формируются их ускорения a и замедления  asтечения, которые будут являться производными при выводе формул прогнозируемых величин - гидродинамических рывка ‘Jh и стопора ‘Sh.

 

Рис. 2. Зависимости изменения скорости Uтекущей жидкости по длине lи времени (t)(при l= 1 м) сужающихся (а, б, в) и расширяющихся (г, д, е) каналах закрытых систем различной формы поперечного сечения.

В результате выполнения комплекса вышеуказанных исследований и на основе использования метода формализации автором были получены новые физические величины, описываемыми формулами.

Спрогнозированные новые физические величины:

гидродинамический рывок (breakthrough accelerated motion in hydrodynamics), м/с³, - векторная физическая величина, характеризующая темп возрастания равноускоренного течения потока или отдельного слоя вязкой жидкости при переходе из одного сужаемого пространства в другое сужаемое пространство закрытой системы (рис. 3):

‘J_h = (a_t –a_o) / t = _delta a_to / t

где ao,  atсоответственно начальное и конечное ускорение потока или отдельного слоя жидкости, возникающие при их переходах в сужаемые пространства закрытых систем (в расчетах принимаются их усредненные значения для каждого сечения или индивидуальные для отдельного слоя жидкости); _deltaaot - прирост ускорения течения потока или отдельного слоя жидкости в обозначенном пространстве;  t – время, за которое переместится поток жидкости или отдельный его слой по длине исследуемого пространства;

гидродинамический стопор (significant hydrodynamic slowing down), м/с³, – процесс обратный гидродинамическому рывку, -   векторная физическая величина, характеризующая темп снижения равнозамедленного течения потока или отдельного слоя вязкой жидкости при переходе из одного расширяемого пространство в другое расширяемое пространство закрытой системы (рис. 4): 

‘S_h = (a_st –a_so) / t = _delta a_sto / t

гдеa_so,  a_stсоответственно начальное и конечное замедление течения потока или отдельного слоя жидкости,  возникающие при их переходах в расширяемые пространства закрытых систем (в расчетах принимаются их усредненные значения для каждого сечения или индивидуальные для отдельного слоя жидкости при: a_so < 0, a_st < 0); _deltaa_sto - прирост замедления течения потока или отдельного слоя жидкости в обозначенном пространстве; t – время, за которое переместится поток жидкости или отдельный его слой по длине исследуемого пространства.

 

Дополнительные новые величины, образованные на основе спрогнозированных величин:

градиент гидродинамического рывка (breakthrough accelerated motion in hydrodynamics gradient), c^-3, - вектор, показывающий направление наибольшего темпа возрастания равноускоренного течения отдельного слоя вязкой жидкости при переходе из одного сужаемого пространства в другое сужаемое пространство закрытой системы, перпендикулярное направлению течения (рис. 3):

_grad ‘J_hi = [(a_ti –a_oi) / t ] / r_срi = (_delta a_toi / t)/ r_срi

гдеa_oi,  a_tiсоответственно начальное и конечное ускорение течения i – го слоя жидкости, возникающие при его переходах в сужаемые пространства закрытых систем (в расчетах принимаются их индивидуальные значения для отдельного i – го слоя жидкости в каждом поперечном сечении); _deltaa_ot - прирост ускорения течения отдельного i – го слоя жидкости в обозначенном пространстве; r_срi - среднее расстояние между i -ми слоями жидкости в исследуемых сужаемых пространствах; t– время, за которое переместится отдельный  i – й слой по длине исследуемого пространства;

градиент гидродинамического стопора (significant hydrodynamic slowing down gradient),  с^-3, - вектор, показывающий направление наибольшего темпа убывания равнозамедленного течения отдельного слоя вязкой жидкости при переходе из одного расширяемого пространство в другое расширяемое пространство закрытой системы, перпендикулярное направлению течения (рис. 4):

_grad‘S_hi= [(a_sti–a_soi) / t ] / r_срi= (_дельта a_stoi/ t)/ r_срi

гдеa_so,  a_st соответственно начальное и конечное замедление течения i – го слоя жидкости, возникающие при его переходах в расширяемые пространства закрытых систем (в расчетах принимаются их индивидуальные значения для отдельного i – го слоя жидкости в каждом сечении, где: a_soi< 0, a_sti< 0); _deltaa_stoi- прирост замедления течения потока или отдельного i – го слоя жидкости в обозначенном пространстве; t – время, за которое переместится отдельный  i – й слой по длине исследуемого пространства; r_срi–среднее по поперечным сечениям расстояния между слоями текущей жидкости.

 

 

Рис. 3.  Профили скоростей, ускорений и рывка при переходе равноускоренного течения слоев жидкости в сужаемое пространство (показана нижняя половина поперечного сечения потока)

 

АA’, ВB’, СC’ – поперечные сечения текущей жидкости; U_A, U_B, U_C – соответственно скорости течений по сечениям АA’, ВB’, СC’; r_ii – расстояния между слоями текущей жидкости на поперечных сечениях;  r_срi– средние расстояния между слоями текущей жидкости по сечениям АВ, ВС и их усредненные значения при рывке;  _grad U_i,  _grada_i,  _gradJ_i – градиенты соответственно скорости, ускорения и рывка. Вертикальными жирными стрелками показаны направления наибольшего возрастания градиентов, а горизонтальной стрелкой направление течения жидкости.

 

  

 

Рис. 4.  Профили скоростей, гидродинамических замедлений и стопора  при переходе равнозамедленного течения слоев жидкости в расширяемое пространство (показана нижняя половина поперечного сечения потока)

АA’, ВB’, СC’ – поперечные сечения текущей жидкости; U_A, U_B, U_C – скорости течений по сечениям АA’, ВB’, СC’; r_срi– средние расстояния между слоями текущей жидкости по сечениям АВ, ВС и их усредненные значения при стопоре;  _grad U_{i,  grad} a_si, _grad S_i – градиенты соответственно скорости, замедления и стопора. Вертикальными жирными стрелками показаны направления наибольшего возрастания градиентов, а горизонтальной стрелкой направление течения жидкости.

На рисунке 5 а, б представлены зависимости гидродинамического рывка ‘J_h, его градиента _grad‘J_h и гидродинамического стопора ‘S_h, его градиента_grad‘S_h, соответственно от прироста ускорения_deltaa и замедления_deltaa_sтечения потока или отдельного слоя жидкости.

 

Рис. 5. Зависимости изменения гидродинамических рывка ‘J_h, стопора ‘S_h(а) и их градиентов_grad‘J_h и_grad‘S_h (б) от прироста ускорения  _deltaa и замедления  _deltaas течения жидкости соответственно в сужающихся и расширяющихся каналах закрытых систем.

График рис. 5 а показывает, что гидродинамический рывок ‘J_h за единицу времени  прямо пропорционален приросту ускорения_deltaa, а гидродинамический стопор‘S_hприросту замедления  _deltaa_sтечения жидкости. Значения их градиентов_grad‘J_h и _grad‘S_h  соответственно пропорциональны приросту ускорения  _deltaa и замедления  _deltaa_s.

Спрогнозированные новые пилотные (пробные) величины ‘J_h, ‘S_h  и образованные на их основе пилотные величины _grad ‘J_h, _grad‘S_h имея полные размерности соответственно LM⁰T³I⁰J⁰θ⁰N⁰R⁰S⁰  и  L⁰M⁰T³I⁰J⁰θ⁰N⁰R⁰S⁰,  временно займут свое место в ячейках №№ 10-22 (строка-столбец) и №№ 10-25 специализированной таблицы логической трехмерной системе СИ [8].    Обеспечить себе постоянное место в системе СИ они смогут после прохождения этапов апробации и обсуждения.

В работе приведен второй пример (первый представлен в работах автора [1-3]) прогнозирования физических величин и получения их закономерностей для отдельного взятого раздела физики – гидродинамики. Многообразие физических процессов в науке, недостаточная изученность отдельных разделов физики, разработанные автором классификация физических величин [5] и логическая трехмерная система СИ [8] дают возможность исследователям с помощью набора относительно простых теоретических методов открывать новые законы физики.

С работами автора [1,2,4] можно ознакомиться на портале журнала «SCI-ARTICLE.RU» и на авторской странице [9]. 

1. Бессонов Е.А. Метод прогнозирования новых физических величин. Электронный периодический научный журнал «SCI-ARTICLE.RU». № 23. 2015. С.74-79. http://sci-article.ru/stat.php?i=1436346211
2. Бессонов Е.А. Формула длины траектории материальной точки./ Физика. Электронный периодический научный журнал «SCI-ARTICLE.RU». № 25. 2015. С.45-47. http://sci-article.ru/stat.php?i=1441353662
3. Бессонов Е.А. Системный метод прогнозирования новых физических величин. System method of forecasting of new physical Units // Научно-технический журнал «Законодательная и прикладная метрология». – Москва, – 2015. - №6 (139). - С.5-9.
4. Бессонов Е.А. Логическая система физических величин. Электронный периодический научный журнал «SCI-ARTICLE.RU». № 15. 2014. С.95-103. http://sci-article.ru/stat.php?i=1416218904
5. Бессонов Е. Многоуровневая система физических величин СИ. Издательство LAP Lambert Academic Publishing. Германия. – 80 c. - 2015 г. https://www.lap-publishing.com/
6. Чугаев Р.Р. Гидравлика. Энергоиздат. –Л.: 1982. 672 с.
7. Механика жидкости и газа: Учебник для вузов / Аверин С.И., Минаев А.Н., Швыдкой В.С., Ярошенко Ю.Г. М.: Металлургия, 1987, 304 с.
8. Специализированная таблица многоуровневой системы физических величин СИ / Е.А. Бессонов. https://cloud.mail.ru/public/Emp3/1dfeVc8KQ (открыть ссылку можно через список литературы авторской станицы [9])
9. Авторская интернет-страница Е.А. Бессонова: http://system-units-si.ru.gg

Комментарии пользователей:

13.03.2017, 8:30 Бондарь Иван Михайлович Отзыв: Тема работы актуальная, работа выполнена на достаточно высоком научном уровне, может иметь практическое применение. Рекомендую к публикации.

27.04.2017, 5:08 Кузьменко Игорь Николаевич Отзыв: В теме уже выбранной автором есть точка роста. И в силу актуальности, стоило бы ее рекомендовать к публикации после прочтения еще узким специалистом в данной области!

Оставить комментарий