Разделы: Математика, Философия
Размещена 15.05.2017. Последняя правка: 16.05.2017.
Просмотров - 3005

Существовать и не существовать

Булыгин Владимир Викторович

нет

Ростелеком

инженер

УДК 510.21

Введение. Быть или не быть – это не только вопрос Шекспира. Это вопрос логики. И, соответственно, математики и всех наук ее использующих. Статья о смысле этих понятий.

Актуальность. В логике понятия существовать и не существовать - основополагающие. С другой стороны, понятия истины и лжи используются повсеместно. Связаны ли они между собой? Да. Понятия истины и лжи трактуются как тождественно истинная и тождественно ложная формулы.

Цели и задачи. Требуется показать на конкретных примерах, что (существует Х) = (Х = Х) = (один Х), (не существует Х) = (Х ≠ Х) = (ноль Х). Показать, что (предикат равенства) можно трактовать как (квантор существования и единственности). И, соответственно, понятие (существует) представляет собой (предикат равенства). А (квантор существования), т. е. (один или более одного) – не тоже самое, что (существует); не то же самое, что (один).

Основная часть. Начнем с главного: с формул тождественно истинных и тождественно ложных. Первые сводимы к (Х=Х), вторые же к (Х≠Х). Чтобы не быть голословным, приведу ниже листинг №1 на языке python. Верность этого кода можно проверить на страничке сайта http://rextester.com/l/python3, выбрав в (Language) python3, затем скопировав текст программы и запустив его на выполнение. Смысл кода – показать предикативность истины и лжи: (Х = Х) - истинно, (Х  ≠ not Х) - истинно, (Х = not Х) – ложно,  (Х ≠ Х) – ложно.

 

#!/usr/bin/python

#Листинг №1

#False - тождественно ложная формула

#True - тождественно истинная формула

myList = ['A', '=']

for X in myList:

    print('Для переменной', X, 'из списка myList')

    print(X != X) #ТЛФ - тождественно ложная формула

                  #вернет False

    print(X == (not X)) #ТЛФ - тождественно ложная формула

                        #вернет False

    print(X == X) #ТИФ - тождественно истинная формула

                  #вернет True

    print(X != (not X)) #ТИФ - тождественно истинная формула

                       #вернет True

 

Здесь тождественно ложные формулы (X != X) и (X == (not X)) эквиваленты. И они же выражают смысл несуществования:  (не существует Х) = (X != X) . Пример с листингом №2 ниже. Единственное замечание: необходимо предварительно в (Show input) ввести либо А, либо нечто отличное от А.

 

#!/usr/bin/python

#Листинг №2

#Пример логики (Х = Х) = (Х существует)

#                           (Х ≠ Х) = (Х не существует)

Х = 'A'

myList = []

myList.append(input('Введите в список: '))

#

if Х not in myList: print('1: в списке не существует Х')

if Х == myList[0]: print('2: в списке существует Х')

else: print('3: в списке не существует Х')

#т.е. в списке (не существует Х), если (Х ≠ Х)

#

#если (Х == not Х), то (Х не существует) &

#если (Х не существует), то (Х == not Х)

 

Эта же логика позволяет сформулировать пустое множество, как множество элементов Х, таких что Х≠Х. И эта же логика демонстрирует, что результатом пересечения множеств является пустое множество, если каждый элемент первого множества не равен каждому элементу второго множества. Листинг №3 ниже.

 

#!/usr/bin/python

# Листинг №3

# логика: (не существует Х) = (Х ≠ Х)

#         (существует Х) = (Х = Х)

A = ('a', 'b', 'c', 'd')

B = ('e', 'c', 'd', 'f')

C = ('g', 'h')

D = ()

#

def set_intersect(set_1, set_2):

    si = False

    for in1Set in set_1:

        for in2Set in set_2:

            if in1Set == in2Set:

                #in1Set == in2Set - т. е. одно,

                # т. е. (существует Х) = (Х = Х) = (одно Х)

                #print(set_1, и set_2 пересекаются: ', in1Set, '=', in2Set)

                si = True

            #else: print('пересечение set_1 и set_2 пусто')

            #поскольку (не существовать = нет хотя бы одного)

            #          (не существовать = не (один или более одного))

    if si == True: print(set_1, ' и ', set_2, 'пересекаются')

    else: print(set_1, ' и  ', set_2, ' не  пересекаются')

    return si

#

set_intersect(A, B) #True: множества A и В пересекаются по элементам 'c', 'd'

                           #Имеем (одно или более одного) равенства.

set_intersect(A, C) #False: множества А и С не пересекаются,

                           #поскольку каждый из элементов множества А

                           #попарно не равен каждому элементу из множества С.

set_intersect(D, D) #False: пустое множество определяется

                           #тождественно ложной формулой (противоречием).

                           #В пустом множестве нет такого элемента X, что X=X.

                           #Сказать, что в множестве не существует элементов -

                           #то же, что сказать, что

                           #каждый элемент Х этого множества такой, что Х≠Х.

 

В этом примере, для определенности, возьмем множество А, каждый элемент которого является единственным: (а – одно, b – одно, с – одно, d – одно). Что значит быть одним? То, что каждый элемент этого множества (равен себе). Это единственное свойство различных элементов множества, которое у них одно и то же. Итак, взаимосвязь алгебры и логики такова: (существует a) = (a = a) = (одно a), (существует b) = (b = b) = (одно b), (существует c) = (c = c) = (одно c), (существует d) = (d = d) = (одно d).

Хочу сказать, что логика (существует, не существует) не только находится в наших головах. Такая логика, образно, встроена в этот мир. Возьмем для примера описание сущего в квантовой механике. Несепарабельность есть неотделимость! Ну, разве это не удивительно? Одна частица может быть в различных состояниях одновременно. В частности, одна и та же частица может быть в различных точках пространства. Чушь? Отнюдь. С точки зрения отстаиваемой здесь логики: частицы нет, если о ней можно сказать, что частица не тождественна себе. Впрочем, об этой странности думал еще Аристотель [3, 35]

 

 

Эта же логика с примитивами (существует Х), (не существует Х) позволяет конструировать более сложные сущности. Не буду касаться тождественно истинных формул, поскольку о их важности сказано многое. Скажу только о тождественно ложных. Пусть имеются однозначно замкнутые преобразования Т и М, как представлены ниже.

 

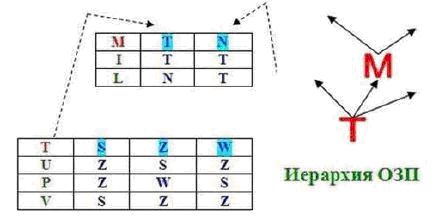
Здесь в табличном виде представлены функциональные зависимости Y=F(X) или, что то же, переходы вида (F: X -> Y). Так, однозначно замкнутое преобразование М – это: (I : T -> T), (I : N -> T), (L : T -> N), (L : N -> T). Кроме того, преобразование Т, как видно из рисунка, является состоянием преобразования М. Что можно сказать об этих переходах? Что представляет собой, например, переход (L : T -> N)? То, что сначала (существует Т), затем (не существует Т & не существует N) и, наконец, (существует N). Итак, где есть изменение – там есть тождественно ложная формула, хоть и в неявном виде.

Мое мнение: область самоусложняющихся алгоритмов с этими (существует, не существует) – эта область, в которой можно и нужно искать механизм возникновения жизни. Такой подход отстаивается в статье [2].

Напоследок хотелось бы привести решение одной из олимпиадных задач по логике. Пример взят из книжки серии международные олимпиады школьников [1, 79].

Островитяне говорят пиф и паф вместо слов да и нет. Причем, неизвестно означает ли пиф – да; или пиф означает нет. Как определить кто есть кто перед тобой: лжец или не лжец? Ответ лжеца будет сконструирован как тождественно ложная формула: (Х ≠ Х) или (Х = not X). Тогда задав вопрос (пиф - это да?), лжец ответит, если на их языке пиф – это да, как не-равно, т. е. (пиф не-равно да). Его ответ: паф. И лжец же ответит, если на их языке пиф – это нет, как равно, т. е. (пиф равно да). Его ответ: паф. Если эти же вопросы адресовать не лжецу, то услышим в ответ пиф.

Научная новизна. В статье показано, что истина выразима тождественно истинной формулой, ложь выразима тождественно ложной формулой. И без этих формул не существует способа описать нечто полным образом. И, таким образом, закон непротиворечия в логике верен только для существующих объектов. Несуществующие же объекты можно выразить тождественно ложной формулой (противоречием).

Результаты и заключение. На примерах показано, что (существует Х) = (Х = Х) = (один Х), (не существует Х) = (Х ≠ Х) = (ноль Х). Разумеется, эта логика работает не только на языке python, но и на любом другом. Поскольку же эти формулы имеют место быть для отображения действительности, то и в самих явления они есть. В частности, в квантовой механике: если нечто находится в различных состояниях одновременно, то это нечто не существует; & нечто не существует, если это нечто находится в различных состояниях одновременно.

1. Башмаков М.И. Математика в кармане кенгуру – М. Дрофа, 2011
2. Булыгин В.В. Энтропия и жизнь с точки зрения логики [электронный ресурс] // URL: http://apriori-journal.ru/seria2/3-2016/Bulygin.pdf
3. Доронин С.И. Квантовая магия [электронный ресурс] // URL: http://www.biophys.ru/archive/books/doronin.pdf

Рецензии:

15.05.2017, 11:20 Поваляев Сергей Анатольевич
Рецензия: Автор в разделе " научная новизна" излагает, что " истина выразима тождественно истинной формулой, ложь выразима тождественно ложной формулой" и далее - " без этих формул не существует способа описать нечто полным образом ".Здесь, по сути, и нет никакой научной новизны . А если новизна лежит в русле описательной формализации авторского концепта, тогда это совсем другое и это надо чётко определить. исходя из поставленной цели статьи. Методологию нарушать нельзя. Советую это учесть и ,возможно, поправить.

15.05.2017, 13:40 Эрштейн Леонид Борисович
Рецензия: Актуальность не обоснована. Не понятно зачем вообще все это нужно. Научная новизна странная, истина выразима истинной формулой. Кто бы сомневался. Вот если бы ложной. А тут все очевидно. Кроме того, тот факт, что автор нечто показал на примерах вообще ничего не доказывает, ибо могут быть контрпримеры. В общем я думаю это надо доработать, показать какую проблему решает автор, показать как по новому он ее решает. А так публиковать нельзя.

15.05.2017, 21:29 Эрштейн Леонид Борисович
Рецензия: Видите ли в чем дело. Тот факт, что я не могу предъявить контрпримеры вовсе не означает, что их не существует. И уж подавно не означает, что их не может существовать. Вы же пишите научную статью, так вот и докажете в ней, что таких контрпримеров не может быть. А пока не докажете, увы, они могут существовать.

16.05.2017, 0:26 Колесникова Галина Ивановна
Рецензия: Поскольку авторская позиция проработана, а основные квалификационные требования соблюдены, то работу можно рекомендовать к публикации.

18.05.2017, 22:33 Мирмович-Тихомиров Эдуард Григорьевич
Рецензия: На взгляд рецензента, абсолютно тривиальные, тавтологические рассуждения, спрятанные в логические формулы и символы, не образуют научную статью, которая не решает ни одной проблемы пусть даже "квантовой логики" (например, искусственно надуманной "кошки Шрёдингера"). Может, автору и кажется, что он сделал какое-то открытие. Это должно хотя бы "казаться" не только ему. Демонстрация владения и применения для тривиально обратимых логических "круговоротов" программой PYTHON вызывает уважение к автору. Однако рецензент не находит достаточных оснований для рекомендации данного материала к опубликованию в данном журнале. Но если другие рецензенты с этим мнением не согласны, то в своей положительной рецензии пусть развеют выраженные здесь сомнения.

19.05.2017, 11:26 Мирмович-Тихомиров Эдуард Григорьевич
Рецензия: Владение программой рецензентом одобрено, но это не наука. Разве рецензент в своих сомнениях в научной ценности текста в чём-то отошёл от текста: "В статье показано, что истина выразима тождественно истинной формулой, ложь выразима тождественно ложной формулой. И без этих формул не существует способа описать нечто полным образом. И, таким образом, закон непротиворечия в логике верен только для существующих объектов. Несуществующие же объекты можно выразить тождественно ложной формулой (противоречием)", являющегося выражением научной новизны самим автором? Объект - это существующий предмет, и нечто не существующее объектом называть никто не решается. Может, в этом смелость автора? Для инженера "Ростелекома" - это особенно должно быть близко. А существование - это философская (да, и бытовая) категория обозначения наличное БЫТИЕ некой вещи в ЧЕЛОВЕЧЕСКОМ ОПЫТЕ. Играть с этими фундаментально аксиоматическими изначально первичными терминами инструментами, аппаратом более вторичного (позднего) изобретения и создания на их основе - дело не благодарное и даже по энтропийной технологии к новым результатам привести не может. Так думает рецензент, несмотря на раздражение автора по поводу не восторженной рецензии. Однако, при одной отрицательной рецензии - 2-4 других положительных (уважаемые Галина Ивановна, Леонид Борисович, Сергей Анатольевич, Оганес Александрович) дают право на публикацию.



Комментарии пользователей:

15.05.2017, 8:16 Булыгин Владимир Викторович Отзыв: По сути, выводы статьи такие же, что и по ссылке http://elementy.ru/trefil/21142/Teorema_Gyodelya_o_nepolnote [если система аксиом полна (то есть любое утверждение в ней может быть доказано), то она противоречива]. Различие лишь в том, что делается вывод: противоречия (тождественно ложные формулы) могут быть объектом логики, что и демонстрируется на примерах.

15.05.2017, 9:05 Булыгин Владимир Викторович Отзыв: Пересечение множеств А и С - пусто. Пусто, поскольку элементы такого множества - это (а=g, a=h, b=g, b=h, c=g, c=h, d=g, d=h), т.е. имеем (все ложно), т.е. каждый элемент пустого множества выражен тождественно ложной формулой

15.05.2017, 11:20 Адибекян Оганес Александрович Отзыв: Адибекян Оганес Александрович. Статья Булыгина В.В. написана по составу математической логики, которая как-то опирается на «формальную логику» или научную, не совпадающую с «диалектической логикой» или философской. Но именно философская логика сопоставляет мысли в составе понятий и суждений и окружающие физические объекты вдобавок к сопоставлению одних мыслей с другими, интересуясь совпадениями или не совпадениями их для ясности истинности мысли, ложности или же неопределенности, дающей гипотезу. У формальной логики иначе. Там сопоставляются одни мысли с другими при известности, ясности, заданности этих вторых в качестве истин, лжи или гипотезы. Математическая логика еще более упрощенная, она имеет дело с количественными показателями и реальностей и мыслей, выражаемыми цифрами, а также их символикой в виде букв, своих цифр. Рецензируемая статья этих вещей не учитывает. Как представляется истинность и ложность, что означает наличие или отсутствие? Если касаться совпадения или отсутствия этого по физическим объектам, то эти объекты могут в чем-то совпадать, и тут же в чем-то не совпадать. Точно также и пара из мысли и физического объекта рассмотрения. Если идти дальше, то это и у пары мыслей. Мне с инженерным образованием, философу, специалисту по логике, знатоку квантовой механике по трудам А.Эйнштейна замысел статьи не совсем понятен. Предлагаю учесть сосу-ществование логики философской, научной и математической, разобраться с различиями в них представлений истины и лжи, а с этим существования и не существования.

16.05.2017, 4:26 Булыгин Владимир Викторович Отзыв: [УДК 510.2 - Основания математики, 510.21 - Общие философские проблемы. Критические аспекты логических антиномий]. К прочим направлениям философии данная статья отношения не имеет.

17.05.2017, 23:24 Parshin Sergey Aleksandrovich Отзыв: Одно из 2-х. Либо автор не корректно сформулировал название статьи, либо поместил не в тот раздел научных направлений. Автор декларативно утверждает, что в данном тексте "новизна есть". Однако, в конкретно данном контексте материалов сайта он обязан использовать понятие новизны не в его специфически им трактуемом формально логическом значении, а в обще употребительном, общенаучном. В противном случае он был бы обязан содержательно обосновать принадлежность данного его утверждения к, им так называемым - "тождественно истинным". Философские аспекты данного круга проблем ("присутствия отсутствия") широко обсуждались, начиная с Парменида и Зенона - более 2 тыс. лет назад. В 20в в контексте философские проблемы мат. анализа и теории множеств. Есть вокруг этого обширная литература. Предлагаю автору попытаться опубликовать этот (доработанный) текст после консультаций со специалистами прикладной математики на предмет его новизны и полезности для выяснения границ эпистемологически адекватной применимости в языках программирования.

18.05.2017, 7:44 Булыгин Владимир Викторович Отзыв: Учебное пособие ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ О. Ю. Агарева, Ю. В. Селиванов [стр 17]. Цитата: Формулу, значения которой для любого набора переменных есть 1, будем называть тождественно истинной формулой (или тавтологией). Формулу, значения которой для любого набора переменных есть 0, будем называть тождественно ложной формулой (или противоречием). ... P.S. Как уже писал ранее, статья написана в рамках УДК 510.21. Обсуждать в терминах ("присутствия отсутствия"), наверно можно, но тогда этот вопрос не к мне и не к этой статье, где действенность этих формул подтверждается. А именно, ими выражено: Х есть, Х нет.

19.05.2017, 11:34 Мирмович-Тихомиров Эдуард Григорьевич Отзыв: Следовало бы добавить, что использование в тексте очень выигрышного термина "полнота", далее нигде не определяется и не адаптируется к рассуждениям автора по проблеме существования, выраженных в логических формулировках. Аксиоматическая полнота без упоминания К. Гёделя, А. Робертсона и др. корифеев не убедительна.

19.05.2017, 12:40 Parshin Sergey Aleksandrovich Отзыв: "ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ О. Ю. Агарева, Ю. В. Селиванов" Авторы Вами цитированной работы не философы, а математики, поэтому в предисловии предупреждают, что данное учебное пособие рассматривает сугубо математические аспекты алгебры логики в рамках дисциплины «Математическая логика и теория алгоритмов» для студентов обучающимся по специальностям «Информатика и вычислительная техника» и «Системы автоматизированного проектирования». Авторы методички, обобщающей конспекты лекций по одному из разделов прикладной математики не претендуют на полноту анализа научных идей, а тем более, новизну выводов. Философские основания в данной работе только упоминаются однажды, но не рассматриваются. Следовательно Ваша отсылка к "идолам Авторитета" (Ф.Бэкон) не работает и в прямом и обратном смысле. Под критериями существования в философии пони мают отнюдь не то же, что в виде внутренне аксиоматической непротиворечивости в логических основаниях математики и, тем более, синтактики языков программирования. Сам этот Ваш текст видимо вполне уместен и полезен как такая же методичка для одной из тем семинарских занятий студентам, обучающимся по специальностям «Информатика и вычислительная техника» и «Системы автоматизированного проектирования». Другие источники Вашего библиографического списока своим уровнем тем более - курам насмех. Увы, но к философской проблематике этот текст прямого отношения не имеет.

19.05.2017, 13:59 Булыгин Владимир Викторович Отзыв: Да что ж такое, Сергей Александрович! Какой Бэкон? Речь в статье идет о логике, а не о философском понимании со времен Парменида. Речь идет о законах, которые применимы. Применимы, в том числе, на независимом от субъективной интерпретации источнике.

19.05.2017, 15:51 Parshin Sergey Aleksandrovich Отзыв: "о логике, а не о философском понимании" Логика, с момента её возникновения, всегда была одной из философски х дисциплин. "Речь идет о законах" В математике нет законов, если под законом понимать объективные связи и закономерности макро космоса вселенной, а не специфику субъективности его отображения в микрокосме рацио. Математика - только один из инструментов построения количественных моделей упорядочивания опыта сознанием. В этом смысле она только идеи об идеях к реальному миру прямого отношения не имеющие. "Применимы, в том числе, на независимом от субъективной интерпретации" Конвенциональный характер этих идей ничего не говорит об их объективности, а, следовательно и об адекватной применимости по отношению к внешнему миру. Наборы аксиом и вытекающий из них "мир" в голове математика по существу произволен. ----- Вам не нравится философская семантика и прагматика, ну так публикуйтесь там, где занимаются абстрактным анализом синтактики и даже иногда воображают будто структуры образуют особый незримый мир чистых форм, или в терминах современной мистики - обсуждают "информационные поля" как особый мир таких "реальностей", которые более реальны чем единственно реальный космос наблюдаемой вселенной.

19.05.2017, 16:12 Булыгин Владимир Викторович Отзыв: В математике есть законы, Сергей Александрович, которыми пользуются не только математики. В отличии от философии, которая которая думает иначе. Это статье размещена с УДК 510.21, т.е. имелось ввиду "основания математики, логические антиномии". К другим направлениям "поговорить" она отношения не имеет. Совсем.

19.05.2017, 16:49 Parshin Sergey Aleksandrovich Отзыв: "В математике есть законы" В тюрьме, говорят, тоже есть "законы". ) "УДК 510.21" Там Вы текст разместили правильно. Тут зачем? Не надо на синонимии слов выкраивать софистику терминов, тем более категорий.

19.05.2017, 22:44 Parshin Sergey Aleksandrovich Отзыв: ИТОГО. Категорически против публикации данного текста в разделе философия. Автор не владеет основами философских представлений о категории существования. Хуже того, c сциентистски ложным апломбом, но по факту прибегая к примитивной софистике и тавтологии, он дискредитирует методологическую значимость и фундаментальный статус философски научного анализа.

20.05.2017, 7:06 Булыгин Владимир Викторович Отзыв: Насколько естественна работа с тавтологиями и противоречиями - пример с алгоритмом Дейкстры (поиск оптимального маршрута). Ссылка: https://github.com/bulygin69/dijkstra/blob/master/dijkstra2.py Наиболее наглядно это видно в условных конструкциях. Например, строчка пятьдесят вторая [52: if not x in p: #если соседа (x) нет в словаре (p)] попросту означает, что проверяется на равенство Х с каждым элементом из списка P: если (Х равно не-Х), то переопределяем метки.

20.05.2017, 9:09 Булыгин Владимир Викторович Отзыв: Есть такое направление философии: аналитическая. Сфера ее интересов - анализ логики и языка. Вот великолепная книжка Российских авторов: АНАЛИТИЧЕСКАЯ ФИЛОСОФИЯ http://yanko.lib.ru/books/philosoph/blinov-ladov-lebedev=analytic_philosophy.htm

6.07.2017, 17:13 Булыгин Владимир Викторович Отзыв: (кот_жив != кот_жив) = (кот_жив = not кот_жив) Теперь к тождественно ложной формуле применим отрицание. .... Получим: not (кот_жив = not кот_жив) = (кот_жив != not кот_жив) ..... А уже (кот_жив != not кот_жив) преобразуемо либо к (кот_жив = кот_жив), т.е. (существует кот_жив) либо к (not кот_жив = not кот_жив), т.е. (существует not кот_жив), т.е (существует мертвый кот) ..... Таким образом, если применяем отрицание к тождественно ложной формуле происходит, говоря языком квантовой механики, СХЛОПЫВАНИЕ - коллапс волновой функции ... либо к кот_жив, либо к not_кот_жив

6.07.2017, 18:40 Булыгин Владимир Викторович Отзыв: Идея циклической вселенной, согласно Пенроузу [По следам тайны большого взрыва https://www.youtube.com/watch?v=-p3PIs7PuVU] в том, что растянутый большой взрыв и сжатая бесконечность выглядят почти одинаково. .... Т.е. он утверждает, что если имеется бесконечно растянутая вселенная с нулевой массой (вследствие ее расширения), то это тоже, что и точка сингулярности (до нуля сжатая вселенная) .... Таким образом, все им сказанное имеет непосредственное отношение к формуле (Х = not Х) со всеми вытекающими из этой формулы парадоксами.

Оставить комментарий