Две дороги к теории множеств

УДК 510.21

Введение. Что, если по иному взглянуть на основы теории множеств? Можно ли трактовать характеристическое свойство как элемент множества? Как выразить логической связкой тоже самое элемент множества и его характеристическое свойство? Вот эти вопросы основания математики и будут рассмотрены ниже под углом зрения аналитической философии, идеалом которой является сведение к минимуму рассуждений интуитивных и неопределяемых.

Актуальность. Трактовка предиката равенства (квантора существования и единственности) в качестве понятия «существует»  делает осмысленным речевые обороты «существует х». А уже это, в свою очередь, допускает трактовку элемента множества (в зависимости от порядка иерархичности): и как аргумента функции, и как значения функции, и как функции.

Цели и задачи. Требуется показать отношения однозначности между характеристическим свойством множества и его элементами. Показать, что язык логики предикатов и кванторов применим и к множествам, представленным иерархично.

Основная часть. Почему не каждая рыба – селедка, но каждая селедка – рыба? Потому что квантор (все) – не то же, что квантор (один или более одного). Потому что в предикативной форме: рыба(селедка) – не тоже, что рыба(не селедка). Потому что с использованием характеристического свойства, которое у них одно, сами элементы множества различны: {селедка, не селедка | рыба}. В учебниках математики, правда, это пример был бы представлен как {х | P(x)}, где P – рыба, т. е. быть рыбой - свойство каждого элемента этого множества. Замечу здесь, что субъект высказывания и предикат могут быть одним и тем же. В таком случае такая запись вырождается в {х | х(x)} или, что то же, в {х | х=х}.

Теперь рассмотрим, для наглядности, множество из биологии. Пусть этим множеством будет {слон, собака, кошка, муха, комар}. В нем можно выделить два подмножества: подмножество зверей {слон, собака, кошка} и подмножество насекомых {муха, комар}. Их можно выразить через характеристическое свойство: {слон, собака, кошка | зверь}, {муха, комар | насекомое}. С формальной стороны здесь следовало бы писать {слон, собака, кошка | зверь(х)}, {муха, комар | насекомое(х)}, но не думаю, что это существенно. Само же множество можно представить как множество животных {слон, собака, кошка, муха, комар | животное} или как объединение двух множеств: зверей и насекомых. Кстати, такое понимание множеств, если иметь ввиду вид сверху, представляет собой диаграммы Венна.

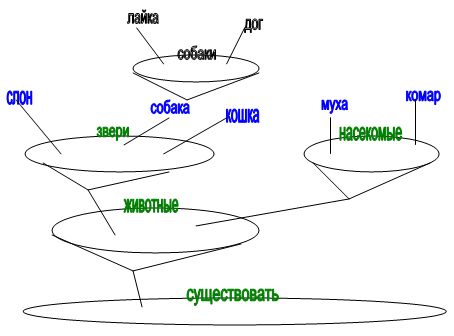
Рис. 1 Иерархия понятий. 

Далее зададимся вопросом: какое характеристическое свойство является общим для любого множества и подмножества? Этот вопрос можно переформулировать: что общего между элементами множества, если о них известно лишь то, что они различны? Такое свойство единственно: каждый элемент множества равен себе. Переводя с математического языка на человеческий, это единственное свойство означает быть, существовать. Итак, имеем множество того, что существует {слон, собака, кошка, муха, комар | существует}. В этом случае его подмножествами будут как животные, так и звери, насекомые.

Хорошо. Но как тогда трактовать пустое множество, ведь оно включено в каждое множество? И вот здесь, словно лист Мёбиуса, логика выворачивается наизнанку. Что не существует – существует или не существует? И то, и другое. Из не существования следует как не существование, так и существование. Из лжи следует как ложь, так и истина. Знакомо, не правда ли?

Что важно? Классический подход исключает трактовку характеристического свойства как элемента множества. Если за элементы множества или подмножества взято выделенное синим цветом на рис. 1 {слон, собака, кошка}, {муха, комар}, то куда, допустим это в дальнейшем потребуется, отнести лайку и дога? Проблема ведь в том, что тогда приходится признать, что собака для лайки и для дога будет являться характеристическим свойством.

Почему же нельзя характеристическое свойство одного множества трактовать как элемент другого множества? Например, почему невозможно представить множество животных, где элементами будут зверь и насекомое как таковые? Потому что такой подход допускает {х | х=х} и {х | х≠х}. Но тождественно ложные формулы, чем противоречия и являются, необходимы для выражения не существования. Полнота описания сущего без этого невыразима. Поэтому возражу в этом моменте Расселу [1]: «cуществует [некий] х», «there is а х» - не бессмысленно. Как и не бессмысленно: «не существует [некий] X», «there is not а X». Что тогда? Трактовать характеристическое свойство как элемент множества где это необходимо? Почему бы и нет! К тому же снимается проблема с догом и лайкой. Получим множество собак {лайка, дог | собака}.

Такой подход практически неограниченно позволяет спускаться и подниматься по иерархии понятий. Ниже, используя его, примеры логики первого порядка.

 (1)

Если каждый (зверь – животное), то хотя бы один (зверь – животное). По формуле (1). Если {зверь(слон), зверь(собака), зверь(кошка) | животное}, то ({зверь(слон) | животное} или {зверь(собака) | животное} или {зверь(кошка) | животное})

 (2) 

Если каждый (зверь – не насекомое), то каждое (насекомое – не зверь). По формуле (2). Если {зверь(слон), зверь(собака), зверь(кошка) | не насекомое}, то {насекомое(муха), насекомое(комар) | не зверь}

 (3) 

Если каждый (зверь – не насекомое), то хотя бы одно (насекомое – не зверь). По формуле (3). Если {зверь(слон), зверь(собака), зверь(кошка) | не насекомое}, то ({насекомое(муха) | не зверь} или {насекомое(комар) | не зверь}) 

 (4)

Если каждый (зверь – животное), то нет такого, что хотя бы один (зверь – не животное). По формуле (4). Если {зверь(слон), зверь(собака), зверь(кошка) | животное}, то нет такого, что ({зверь(слон) | не животное} или {зверь(собака) | не животное} или {зверь(кошка) | не животное})

 (5)

Если каждый (зверь – не насекомое), то нет такого, что хотя бы один (зверь – насекомое). По формуле (5). Если {зверь(слон), зверь(собака), зверь(кошка) | не насекомое}, то нет такого, что ({зверь(слон) | насекомое} или {зверь(собака) | насекомое} или {зверь(кошка) | насекомое})

Отмечу здесь, что {зверь(слон) | насекомое} есть пустое множество, поскольку нет такого слона, который был насекомым.

В этих примерах Х – связанная переменная. Ее значениями являются элементы (слон, собака, кошка, муха, комар). Но возможно за Х принимать также элементы множества {зверь, насекомое | животное} или элементы множества {лайка, дог | собака}, передвигаясь по иерархии понятий.

Поскольку понятие существует в этой статье  понимается как предикат равенства, то законы де Моргана в этой связи можно прочесть следующим образом.

 (6)

 (Верно, что каждое Х - существует) эквивалентно тому, что (неверно, что хотя бы одно Х – не существует). По формуле (6).

 (7) 

(Верно, что хотя бы одно Х - существует) эквивалентно тому, что (неверно, что каждое Х – не существует. По формуле (7)

Стоит заметить, что в отношении формулы х=х можно выделить два момента: что Х - это Х, т. е. Х(х); что Х - равен себе, т.е. =(х). И только если субъектом высказывания является само понятие существует, формула х=х примет вид (=)=(=).

Вот пример программы, который показывает отношения существования. Чтобы убедиться в ее результатах достаточно на страничке сайта [3] в (Show input) ввести два понятия из словаря G.

#!/usr/bin/python

G = {

  'лайка' : 'собака',

  'дог' : 'собака',

  'слон' : 'зверь',

  'собака' : 'зверь',

  'кошка' : 'зверь',

  'зверь' : 'животное',

  'насекомое' : 'животное',

  'муха' : 'насекомое',

  'комар' : 'насекомое',

  'животное' : 'существует',

  'существует' : 'существует'

}

sx, sy = [], []

x, y = map(str, input('Введите два понятия через пробел: ').split())

x1, y1 = x, y

sx.append(x)

sy.append(y)

#

while x != 'существует':

    p = G[x]

    sx.append(p)

    x = p

while y != 'существует':

    p = G[y]

    sy.append(p)

    y = p   

if x1 in sy:

    print(y1, 'есть', x1)

if y1 in sx:

    if x1 != y1:

        print(x1, 'есть', y1)      

Так, если ввести (дог насекомое), то программа ничего не вернет (поскольку дог не есть насекомое, насекомое не есть дог). Если ввести (животное лайка), то программа вернет (лайка есть животное). Если ввести (зверь зверь), то программа вернет (зверь есть зверь).

Замечу, что мы говорим (каждый зверь), имея ввиду  слона, собаку, кошку. Или говорим (некоторое животное)  - зверь, имея ввиду слона, собаку, кошку, муху, комара. И это понятно, поскольку рассматриваются отношения однозначно (каждый) или неоднозначно (некоторые). 

Как исключить неоднозначность? Понятно, что (лайка – собака) и (дог – собака) однозначно. А как быть с (собака – дог) или (собака – лайка)? Устранить неоднозначность можно, если принять во внимание, что характеристическое свойство и элемент множества могут быть связаны через функцию.

Обобщенно: лайка = f(собака), дог = g(собака). Или согласно толкового словаря Ожегова [2], имеем определения. Лайка – то же, что собака, если она породы ездовых, охотничьих или сторожевых. Дог – то же, что собака, если она самая крупная короткошерстная служебная. Условные конструкции в этих определениях задают функции, которые однозначно преобразуют характеристическое свойство в элементы множества. Итак, эти отношения с учетом функций (f(собака) - лайка), (g(собака) – дог) уже однозначны.

Есть еще один момент высказывания Рассела [1], который хотелось бы затронуть:

«Если бы случилось так, что греков не было, то и пропозиция (Все греки являются людьми), и пропозиция (Ни один грек не является человеком) были бы истинными. ...

Пропозиция (Ни один грек не является человеком) - это, конечно же, пропозиция (Все греки не являются людьми). Если бы случилось так, что греков не было, обе пропозиции были бы истинными одновременно». 

Кратко запишем то, что изложено Расселом:

1. Греки – не существуют.

2. (Все) греки – люди.

3. (Ни один грек – не человек) = (все греки – не люди)

4. Для (Греки – не существуют) истинно как (все греки - люди), так и (все греки – не люди)

Комментарий к сказанному Расселом:

5. Рассел отвергает такую конструкцию, поскольку она противоречива, поскольку такая конструкция (все греки - люди)= (все греки – не люди) всегда ложна, т.е. всегда False.

6. Но что есть пустое множество? Пустое множество – это множество, в котором не существует элементов и выражено оно именно как {Х | X ≠ Х}, т.е. это множество, в котором каждый элемент не равен себе. Эта формула (Х не-равно Х) всегда ложна. Согласно же определения самой математики, формула, которая всегда ложна, является ПРОТИВОРЕЧИЕМ!.

Замечу еще только, что Y=F(X) можно прочесть и как Y существует (Y есть), и как F(X) существует (F(X) есть). Когда же говорится (Y есть X), то неявно подразумевается, что  (Y есть X при какой-то функции). При этом, если X=0 и Y=1, то функция F, т.е. отрицание, будет являться, говоря физическим языком, коллапсирующей функцией: 1 = not(0), существует Х = not (не существует Х). Именно отрицание not преобразует нечто, находящееся в различных состояниях (Х = not Х), либо в (существует X), либо в (существует  not X). Поскольку not (Х = not Х) - тоже, что (X != not X). Имеем либо (существует Х), либо (существует not X): (X != not X) = (Х = Х) либо (X != not X) = (not Х = not Х)

Научная новизна. Характеристическое свойство множества и элемент множества могут трактоваться как одно. Возможны варианты. Либо характеристическое свойство множества является элементом другого множества. В этом случае такой подход представляет иерархию множеств. Либо, если рассматривается только одно множество, это выражает свойство элемента существовать. Кроме того, элемент множества может быть выражен через логическую связку то же самое с характеристическим свойством множества, если учесть условие (функцию), которая однозначно преобразует характеристическое свойство в элемент множества.

Вот еще любопытные выводы, вытекающие из рассмотрения тождественно истинных и тождественно ложных формул.

Сравниваем: (1 = 0 + 1) и (1 = not 0). Замечаем, что (not) = (+1).

Именно используя это notp (отрицание по отношению к каждому предыдущему числу), программа run_nr_i конструирует числа натурального ряда, не используя явно +1. Причем, notp вырождается в простое отрицание not для случая, если предыдущим числом является только число ноль. 

С учетом того, что (1 = +1), (-0 = 0 = +0) имеем: (notp (notp 0))  = 2. Поскольку (notp 0) = +1 +0 = +1 = 1, (notp 1) = (+1 +1) = 2

Что касается минуса: поскольку (нет Х) = (Х ≠ Х) и (нет Х) = (Х - Х), то (Х - Х) = (Х ≠ Х). Из (Х - Х) = (Х ≠ Х) следует, что (минус = не-равно). Так, из 3 – 3 = (3 не-равно 3) следует 3 = (3 не-равно 3) + 3. Получаем 3 = (3-3)+3.

Соответственно: not (Х не-равно Х) = (Х равно Х). Следовательно: not (нет Х) = есть Х, not (ноль Х) = один Х.

Поэтому формула (notp (notp 0))  = 2  может принять вид: (notp (notp (Х не-равно Х))) = 2 Х

Результаты и заключение. Безусловно, концепция спорна. Спорна, поскольку требует переосмысления понятия элемента множества, тем  более, что понятие элемента множества относится к неопределяемым понятиям математики. Но она действенна. И она дает результат. 

Рецензии:

9.09.2017, 12:07 Мирмович Эдуард Григорьевич
Рецензия: Из данной статьи может быть признана актуальной лишь одна мысль: "Безусловно, концепция спорна. Спорна, поскольку требует переосмысления понятия элемента множества". Какого? И конец статьи как раз в разделе "Результаты", что эта концепция "даёт результаты". Если их нет в результатах, то какие результаты? Ни актуальности, ни научной ценности, ни практического приложения этой статьи рецензент не видит. А дискуссия вокруг неё состоит лишь из дополнительных многословных рассуждений автора. Рецензент не рекомендует к публикации данной статьи.