Статья опубликована в №60 (август) 2018
Разделы: Астрономия
Размещена 08.08.2018. Последняя правка: 21.09.2018.
Просмотров - 2548

ВЗАИМОСВЯЗЬ РАЗМЕРОВ АТОМА И ОРБИТ ПЛАНЕТ В СОЛНЕЧНОЙ СИСТЕМЕ

Сахненко Виктор Григорьевич

-

ДИА

Ректор

УДК 521.32

Введение. Еще в 18 веке  И. Тициусом и И. Боде была  предложена дискретная зависимость расстояния  от  Солнца до планет в астрономических единицах 0.4 + 0.3 * 2^k. Значения k для планет: Меркурия -   ∞  , Венеры -0, Земли -1, ... , Урана - 6, Нептун выпадает, Плутона - 7. Однако как видим, эта зависимость определяла орбиты не всех планет и  М.М. Ньето предложил новую закономерность [1].  Согласно этой закономерности соотношение между орбитами соседних планет R_i и R_i+1 равно

 

                     R_i+1 / R_i = a.             (1)

 

     Здесь: a – некоторая постоянная.  Для планет Солнечной системы a  ≈ 3^1/2. Эта закономерность более точно описывает орбиты соседних планет. Однако  возникает вопрос.  Какую орбиту принять как исходную? Очевидно что, поскольку гравитационное взаимодействие  прослеживается до размеров атома (в структуре атома доминирует уже электромагнитное взаимодействие), то исходным радиусом орбиты могут являться параметры атома [2]. И тогда закономерность формирования орбит планет приобретает законченный вид.

Вероятный радиус R_i  орбиты i  планеты в Солнечной системе равен:

      R_i =  w  R_a a ⁱ .          (2)                                                               

          Здесь:  w- отклонение от среднего,

                         R_a = 5.291773^. 10^-11 м – радиус Бора.
                         a = 3^1/2 ,       
                         i  = 0, 1, 2,… – целые числа.  

     

     Полученные результаты достаточно хорошо согласуются с известными параметрами  планет и их спутников (табл. 1). Так для орбит 10 планет, включая планету Церера, среднее значение w_с = 1.00163 ! , при дисперсии d ² = 0.0167, для орбит 59 спутников планет  w_с  =  0.941, d ²  =  0.0239,  даже для радиусов планет и Солнца  w_с  = 0.909, d ²  =  0.0136.  Интересно, что радиусы диффузных планет и Солнца более соответствуют расчетным по приведенной закономерности, чем планеты с твердой поверхностью. Причиной этому  является особенность природы формирования планет с твердой поверхностью и диффузных [3,4]. Поскольку, газовые оболочки диффузные планеты находятся в динамически уравновешенном состоянии, то взвешенные частицы газа легче откликаются на фактор формирующий орбиты планет и их поверхности согласно настоящей закономерности. Существенные отклонения лишь у Сатурна. Причиной этому очевидно являются более мощные и в настоящее время еще неизвестные явления. 

     Центры тяжести систем состоящих из Солнца и планеты также подвержены градации. Среднее значение для всех планет составляет 0.956, при дисперсии d ² = 0.0172.

 

Таблица 1.
Параметры Солнечной системы

 

w* - отношение реального параметра планеты к вероятному.

       Интересно отметить, что радиусы диффузных планет  представляют собой сферические оболочки радиуса R_i, за которыми следует ожидать следующие оболочки радиусом R _i+1. Между этими оболочками вписывается куб. Сторона этого куба равна 2 R _i (рис.1). Его грани опираются на меньшую оболочку, а вершины упираются в большую оболочку.  Вероятные орбиты планет и радиусы оболочек совпадают. Это позволяет предположить, что вероятные орбиты планет располагаются на оболочках, между которыми вписываются кубы. И говорить уже не о вероятных орбитах,  а о вероятных оболочках орбит планет, на которых располагаются вероятные орбиты. Причем этот процесс прослеживается до размеров атома водорода (радиуса Бора).

 

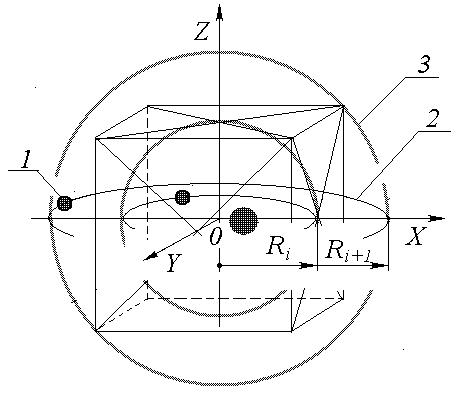
Рис. 1. Вероятные оболочки планет и орбит планет.

1 – планеты и Солнце, 2 – вероятные орбиты планет, 3 – вероятные оболочки орбит планет.

 

        Установленная связь между атомами и параметрами Солнечной системы свидетельствует о едином, по своей природе, формирующем структуру микро и мега мира во Вселенной факторе.

        Объяснить этот феномен можно исходя из классической физики.  Для этого будем полагать, что w  = 1, а соответствующие орбиты R _i  вероятные. Рассмотрим в Космосе взаимодействие некоторого сферически симметричного  массивного тела радиуса   R₀  =  1 и относительно тела легких подвижных частиц. Пусть частицы находящиеся на большом расстоянии от тела,  увлекаемые гравитационным полем тела у его поверхности  приобретают скорость V₀,   (|V₀ | =    U  ^{1/ 2},   U  -  здесь  гравитационный потенциал на поверхности тела)  
       При этих же условиях на  i  орбите  орбитальная скорость V_i  определится по зависимости:

 

           V_i = V₀ 3 ^{– i / 4} .                           (3)  

 

       Поток этих частиц (как поток газа) может растекаться по поверхности сферического тела с тангенциальной скоростью V_t  (первой космической скоростью), либо ортогонально со скоростью V_b.  Будем считать, что  |V₀ |  =  |V_t|  =  |V_b| = 1. Заметим, что скорость V₀₁ освобождения (вторая космическая скорость)  равна

                                                

        V₀₁ = V_t   + V_b.                             (4)

 

       В нашем случае  |V₀₁ | = 2 ^{1 / 2}. Частица с такой скоростью по параболической траектории будет удаляться от центрального тела. Упростим задачу и  криволинейную траекторию частично заменим прямой линией.  Аналогично со скоростью освобождения V₀₂  может от центрального тела удаляться и противоположная частица. На расстоянии  R = (1² + (2^1/2)² ) ^1/2 = 3^1/2 , в точке F₁  векторы скоростей V₀₁ и V₀₂ частиц пересекутся. Со стороны Космоса  частицы, попадая в поле тяжести тела,  вблизи  его поверхности  приобретут  скорость равную скорости освобождения  - V₀₁  и  -V₀₂ соответственно. Как со стороны тела, так и со стороны Космоса векторы скорости освобождения будут образующими конусов с вершинами в точке F₁. Со стороны тела основание такого конуса S₀ , а стороны Космоса основание такого конуса S₁. Любая частица, проходящая через основание конуса S₁ и вершину F₁, обязательно в конечном случае попадет на поверхность тела. И наоборот частица, со скоростью освобождения покидающая тело в пределах рассматриваемого конуса и проходящая через точку F₁ пройдет через основание конуса S₁.  Таким образом, частицы концентрируются в точке F₁ , и при динамическом равновесии образуют в окрестности исходной сферической поверхности тела,  оболочку “1” с повышенной плотностью частиц.

     Этот процесс может повториться и относительно образовавшейся оболочки может быть сформирована новая оболочка “2”  и т.д. Как видно из рисунка на каждой последующей оболочке  (S₂) отображаются предыдущие оболочки (S_2,1). Надо полагать, что оболочки формируются до размеров тел с твердой поверхностью. Например, для Земли конечной оболочкой будет сама Земля.

         Обращает на себя внимание и тот факт, что скорость распространения продольных сейсмических волн v_p вблизи поверхности Земли близка первой космической скорости Земли,   т.е.   |v_p|  ≈  |V_t |= |V_b|. Очевидно, что параметры Земли формируется  Космосом и подобным образом формируются и атомы.  Таким образом,  атомы и их компоненты стабильные элементарные частицы не являются автономными и неизменными, образованиями,  а образуются и поддерживаются вследствие динамически уравновешенного процесса, а именно  обмена микро - частицами,  между телом и Космосом.

       Ожидаемая плотность газа в оболочке условно показана заштрихованными треугольниками (рис.2), а ее толщина  L_i  определяется по формуле

 

 L_i = k R_i = k R_a a ⁱ .                      (5)

 Здесь:  k = ( a - 1) / ( a + 1).  Если  a  =  3 ^1/2, то  k  =  0.268. 

           

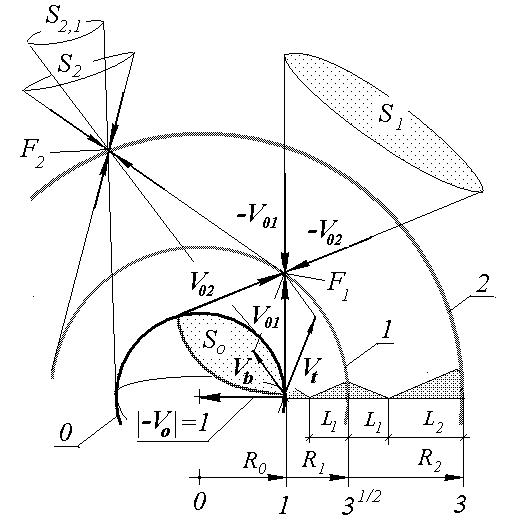
Рис. 2. Формирование оболочек в окрестности сферически симметричной  массы.   

        Заметим, что подобное    соотношение  k  между радиусом оболочки и ее толщиной (рис. 3)  наблюдается в планетарных туманностях, состоящих из ионизированной газовой оболочки и центральной звезды [4]. 
 

Рис. 3. Планетарная туманность. Созвездие Наугольник.

 Shapley 1 (Шепли 1, PLN 329 2.1).

         Для фиксированного значения k = 1,  при i >80  область изменения a = 3^1/2  ± 0.0026. 

    Очевидно, что  процесс установления  планеты на ее вероятную орбиту длительный. Можно полагать, что чем больше отклонение орбиты планеты от ее вероятной орбиты, тем она позже вошла в Солнечную систему  как, возможно  Плутон. Либо  планета испытала мощное воздействие со стороны. Как,  возможно Марс, в момент катастрофического разрушения гипотетической планеты Фаэтон. Часть ее обломков образовала кольцо астероидов и планету Церера. Обломки Фаэтона, попадая на Марс, возможно это и нынешние спутники Марса - Фобос и Деймос, могли сдвинуть его  с вероятной орбиты  ближе к Солнцу.

Вероятный  период  T_i обращения  i  планеты по отношению к периоду частицы  на радиусе Бора  Т₀ , при этом гипотетически вся масса Солнца сосредоточена в сфере радиуса Бора,  определится по формуле

 

          T_i = T₀ 3 ^{3 i /4}.                   (6)

 

           Для Солнечной системы T₀ = 2.094 10 ^-25 c., а вероятный период обращения Земли  T₉₀  =  1.066 года. Аналогично  V₀  = 1.58773*10¹⁵ м / с,  а вероятная скорость на орбите Земли V₉₀  =  29211 м / с.

      Интересна в этом плане гистограмма (рис.4.)  радиусов орбит более 2.27 тысяч экзопланет  [6], среднее отклонение от вероятной орбиты w_с = 0.983, число интервалов 50.    Как видно из рисунка частота орбит экзопланет  вблизи вероятных орбит довольно равномерна.   Это свидетельствует о том, что влияние на формировании вероятных орбит планет оказывается как со стороны Космоса, та и  со стороны звезды (атомных ядер), а сам процесс формирования орбит глобален во  Вселенной.

       Для экзопланет которые расположены в направлении центра Галактики (созвездие Стрельца)   w_c= 0.977, а вероятный  радиус Бора R_ac  будет равен R_ac  =  R_a/  w_c = 1.024 R_a.  А для экзопланет которые  расположены  на периферии  Галактики  (созвездие Тельца),  w_c= 0.961,  вероятный радиус Бора R_ap   составит  R_ap=  R_a/  w_c = 1.04 R_a.  Это свидетельствует о том,  что параметр атома водорода, (вероятный радиус Бора) в сторону центра Галактики уменьшается. Видимо здесь сказывается возрастающий гравитационный потенциал к центру Галактики. И природа этого процесса  подобна  уменьшению размеров планет  по мере того как они  приближаются к Солнцу,  где напряженность гравитационного поля также возрастает  [2,3].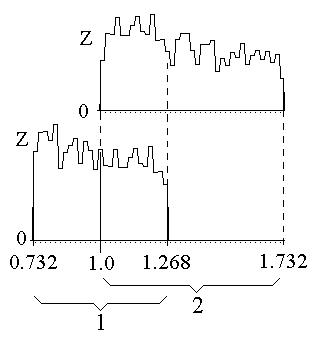  

Рис. 4. Гистограммы частот радиусов орбит экзопланет.

1-  диапазон равен толщине оболочки,  2- диапазон между соседними орбитами. Вероятная орбита 1.0. 0Z –  частота экзопланет.

     

       При неподвижной оболочке относительно ее тела (Солнца) она концентрична, центры тяжести оболочки и  тела совпадают. Однако при  вращении оболочки относительно  тела  ее концентричное положение динамически неустойчиво. Центры тяжести оболочки и  тела смещаются (рис. 5).

 

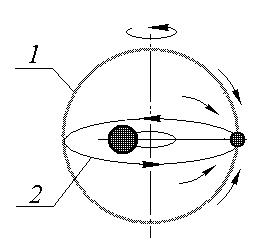
Рис. 5. Стекание частиц к планете по вероятной оболочке.  

1 – вращающаяся вероятная оболочка Солнца, 2- вероятная орбита планеты.

                         

Массы,  составляющие оболочку, под действием на поверхности оболочки дополнительно возникающих центробежных сил стекаются  в наиболее удаленную точку от центрального тела, концентрируются и образуют новое тело (планету).
         Полезно заметить, что   все 10 планет Солнечной системы  включая  планеты Церера и Плутон занимают строго по порядку свои вероятные орбиты, поэтому разумно чтобы все они  имели статус планет. И нет смысла давать этим планетам другой статус  "астероид",  "плутоид" и т.д.  [7,8].

       Вероятные орбиты планет относительно атома  автор просит впредь называть орбиты Сави.  

           Выводы. Атом водорода, Солнце, диффузные планеты  и   орбиты планет в Солнечной системе формируются и поддерживаются в динамическом равновесии  в масштабах Космоса. Установленная взаимосвязь между формированием радиусов планет их орбит  и параметром атома водорода указывает на глобальность этого процесса.    

1. Ньето М М Закон Тициуса-Боде. История и теория. Пер. с англ. М: Мир, 1976. 190 с.
2. Сахненко В.Г. ФОРМИРОВАНИЕ ОРБИТ ПЛАНЕТ В СОЛНЕЧНОЙ СИСТЕМЕ // Научные исследования №4 (23). 2018. (Россия . Москва. 4 августа 2018).
3. Сахненко В.Г. КРИТЕРИЙ ФОРМИРОВАНИЯ ДИФФУЗНЫХ ПЛАНЕТ. // Научные исследования №8(19). 2017. (Россия. Москва. 4 сентября 2017).
4. Сахненко В.Г. КРИТЕРИЙ ФОРМИРОВАНИЯ ДИФФУЗНЫХ ОБЪЕКТОВ. [Электронный ресурс] // SCI-ARTICLE.RU. №48 (август) 2017 URL: http://sci-article.ru/ (Дата обращения: 19.06.2018).
5. Список планетарных туманностей. [Электронный ресурс]. URL: https://dic.academic.ru/dic.nsf/ruwiki/1637411 (Дата обращения: 10.05.2018)
6. [Электронный ресурс]. URL: Open Exoplanet Catalogue. www.openexoplanetcatalogue.com/‎28 Nov 2017 ... (Дата обращения: 10.05.2018)
7. Soter S. (2006). «What is a Planet?». The Astronomical Journal 132 (6): 2513–2519. arXiv:astro-ph/0608359. DOI:10.1086/508861. Bibcode: 2006AJ....132.2513S.
8. AU 2006 General Assembly: Result of the IAU Resolution votes. IAU (News Release — IAU0603) (24 August 2006).

Рецензии:

20.09.2018, 0:55 Мирмович Эдуард Григорьевич
Рецензия: Не вдаваясь в анализ деталей, рецензент видит у автора интерес, титанический труд, креативные подходы и глубокие знания в области ближнего и дальнего Космоса. Жаль, не приведено само соотношение Тициса-Боде (двух Иванов), про "дыру" между Марсом и Сатурном (поясе астероидов от разрушенно планеты "Фаэтон") не сказано (или рецензент пропустил). Работа научна, интересна и подлежит публикации.

21.09.2018, 20:10 Мирмович Эдуард Григорьевич
Рецензия: Уважаемый Виктор Григорьевич! Статья пусть будет опубликована. Но имейте, пожалуйста, в виду. Без слов "третий закон Кеплера" и "постоянная тонкой атомной структуры альфа" тема о совместном анализе вращательных констант от атомной структуры до макромасштабов адекватно раскрыта быть не может. Это Вам напутствие, если захотите им воспользоваться. Тогда статья сможет претендовать на публикацию в "большой литературе". С уважением.

24.09.2018, 16:22 Мирмович Эдуард Григорьевич
Рецензия: Обратите внимание, что альфа - величина безразмерная 1/137, а кеплеровскую константу для всех орбит солнечной системы надо ещё пронормировать.

25.09.2018, 13:27 Мирмович Эдуард Григорьевич
Рецензия: И не только. В микропространстве (да, и вообще в мире) не может быть столько универсальных констант: и с, и h, и аlfa и ещё 200 законов сохранения для элементарных частиц и субчастиц. Пока это "нобелевцы" и "коллайдоровцы" не осознают - продвижения реального в познании, а главное в пространственно-временном прогнозе ожидать не приходится. А пока развитие нашей фундаментальной науки заключается в следующем: как только что-то непонятное наблюдается хоть где, так надо придумать новый кухонно-бытовой термин типа "дыра", "стринги" (слава богу, не женские), "кварки" "глюоны" и цвета частиц... Жаль, что пока опасным и ужасным частицам термин "трампы" не ввели, но, наверное, введут. Извините, но меня это всё (не всегда) стало раздражать. Наукой стало умение запутать простую проблему. Математика имеет две миссии. Одна - помочь продвинуться в объяснении фактов, прогнозе. Другая - в украшении запутанными формулами практически общеизвестное, а иногда и непонятное.



Комментарии пользователей:

Оставить комментарий