Разделы: Педагогика, Математика
Размещена 04.05.2019. Последняя правка: 04.05.2019.
Просмотров - 3061

Методика развития математических способностей

Кудрина Анна Игоревна

бакалавр

ГБОУ ВО "Ставропольский государственный педагогический институт"

студент

Клочко Ксения Александровна, студент 3 курса, факультет дошкольное и начальное образование ГБОУ ВО Ставропольский государственный педагогический институт. Научный руководитель: Кокорева Валентина Владимировна, кандидат физико-математических наук, доцент кафедры математики и информатики, ГБОУ ВО Ставропольский государственный педагогический институт

УДК 51

Введение

Способность мыслить есть у любого человека, но каждый из нас уникален и имеет свои особенности. Вряд ли найдется человек, который с уверенностью может сказать, что от родился с любовью к цифрам и интегралам, или с первых мгновений жизни мог дирижировать оркестром. Но, тем не менее существует устойчивое мнение, что люди с рождения имеют предрасположенности либо к логике, либо к творчеству. Человек развивается всю жизнь, и при должном подходе любой в состоянии освоить творчество или же понять мир математики.

Актуальность
Для решения этого вопроса существуют сотни и сотни различных методик, но, в случае с последним, всегда встает вопрос – с чего начать?

Цели: сформировать представление о математических способностях и представить несколько методик по их развитию

Задачи:
1. раскрыть понятие математических способностей;

2. Представить виды математического мышления

3. представить несколько видов упражнений по развитию математических способностей

Методы: работа с литературой

Материалы: интернет источники, научная литература

Научная новизна: данная работа систематизирует и концентрирует знания по выявлению и развитию математических способностей на разных возрастных этапах

Сперва необходимо понять, что в любом варианте действий необходимостью будет развитие умения работы с цифрами и логическими задачами. Наличие или отсутствие «таланта» не определяет успех работы при должном усердии. Так на первый план станет осознанное решение проводить простейшие математические операции не на калькуляторе, а мыслительно. В случае затруднений не стоит пренебрегать услугами специалистов, способных подобрать оптимальный для каждого вариант успеха, и упростить весьма сложную задачу по развитию математических способностей. Это так уже лишь потому, что решения большинства математических операций – это, в первую очередь, понимание их сути. Мало знать правила, необходимо разобраться в деталях и освоить принцип работы с математическим материалом.

Работа упростится если определить свой тип математического мышления. Всего их пять:

• Топологическое. Это мышление закрепляется ещё в 2 – 3х летнем возрасте и определяет целостность и продуманность всех логических решений. Люди, сохранившие его, чаще всего выделяются дотошностью к деталям. Они тысячи раз продумают каждый шаг, и только после этого сделает выбор.

• Порядковое. Оно отвечает за последовательность и точность всех логических операций. Личности, обладающие таким типом мышления, отличаются бескомпромиссностью в своих решениях, упрямством. Даже если они не сделали все сразу правильно, то да самого конца, неуклонно будут следовать первоначальному плану, даже если это не приведет к успеху.

• Метрическое. Как и последующие развивается сразу после предыдущих двух и обеспечивает человека пониманием чисел и работы с множествами. Люди такого типа отрицают любую неясность сведений, приводя всё к точным цифрам, и только тогда спокойно ориентируются в ситуации. Они всегда наперед просчитывают каждый свой шаг.

• Алгебраическое. Определяет конструкторов и координаторов. Преобладание данного типа мышления гарантирует обладателю нетерпение к правилам и шаблонным действиям. Такие люди способны в любой момент остановиться, приступить к новой работе и, вернувшись к старой, продолжить без потери продуктивности. Они часто подвержены рассеянности, что легко устраняется развитием памяти.

• Проективное. Его можно назвать необходимым для каждого человека, ввиду того, что это мышление дает возможность смотреть на вещи под разными углами и принимать нестандартные решения, способные спасти ситуацию с полной уверенностью в их правильности, хотя они могут нести риски для деятельности.

Перечисленные выше типы мышления имеются у каждого человека, но в разной степени развитости. Найти же свой преобладающий мыслительный тип поможет наблюдательность и огромное количество тестов в Интернете. Благодаря этому можно проследить за своими собственными действиями и ещё чуть больше узнать о себе и своих способностях.

Данные выше типы мышления развиваются полностью у детей к младшему школьному возрасту, развить их можно только занимаясь с ребёнком, уделяя ему время, ведь заложив эти способности и дав им развитие, можно воспитать всесторонне развитую личность. При ознакомлении с рекомендациями у родителей и педагогов появляется ряд вопросов: когда начинать заниматься? как увлечь ребёнка? какие применять методы и упражнения при развитии математических способностей?

По мнению многих педагогов-практиков, начинать заниматься с ребёнком развитием математических представлений, нужно как можно раньше, оптимальным возрастом можно считать 1-3 года. В дальнейшем уже будет намного проще работать с уже сформированной элементами математического мышления.

Начиная развивать у ребенка математические способности, многие родители считают, что математика его не заинтересует, и таким образом неосознанно прививают эту мысль детям. Поэтому занятия должны быть интересными, они должны увлекать ребёнка. Рекомендуется использовать понятия, которые ближе ребёнку, встречаются в обиходе – игрушки, природные материалы, бытовые предметы и т.д. Так же развитие математических представлений можно включать и в досуговую деятельность, использовать интересные, наглядные учебные материалы. Можно использовать и современные информационные технологии, различные онлайн тренажёры и игры. И, конечно же, необходимо чередовать умственную деятельность и физические нагрузки.

Какие же методы и приёмы применять при занятиях по развитию математических способностей с детьми? В основном, по современным методикам, работа должна включать: игровые методы, моделирование, конструирование и сюжетно-ролевую игру. Развивающие игры представляют собой - игры, способствующие развитию умственных способностей: головоломки, ребусы, задачи-шутки. В основном специалистами рекомендуются такие методические материалы, как:

• Блоки Дьенеша

• Палочки Кюизинера

Блоки Дьенеша - интересная, универсальная развивающая игра, которая очень нравится детям. Она позволяет развить: пространственные представления, представления о форме, цвете и размере предмета, творческие способности детей.

С помощью палочек Кюизинера детей легко подвести к осознанию отношений больше-меньше, научить делить целое на части и измерять объекты условными мерками, поупражнять в запоминании состава чисел из единиц, подойти вплотную к сложению, умножению, вычитанию и делению чисел.

Рассматривая развитие математических способностей в начальных классах, стоит отметить, что данные навыки также совершенствуются на занятиях в классе. В этом помогаютют задачи повышенной трудности, занимательный материал, логические головоломки, которые необходимо применять и во внеклассной деятельности и дома. В школьном возрасте детям так же необходимо давать задания практической направленности, например, пол в комнате имеет прямоугольную форму со сторонами 5м и 6м, сколько квадратных плиток со стороной 1м понадобится для настилки пола в комнате. Так же после прохождения какой-либо темы в школе, ребёнку можно предложить углубить свои познания по этой теме. Например, предложить задания на измерение длинны старинными мерами – пядь, локоть, сажень, дюйм и т.д. Можно включать и математические софизмы – утверждения, в доказательстве которых кроются незаметные, тонкие ошибки. Например: 5 и 3 – два разных числа, 3 и 5 равно 8, значит, 8 является двумя разными числами. На первый взгляд рассуждение правильное, но в нем смешаны неравные вещи: первая часть рассуждения – это перечисление чисел, вторая – операция сложения. Между первым и вторым знак равенства поставить нельзя, а значит, это является нарушением закона тождества.

Существует огромное количество упражнений для развития математических способностей. Можно выделить некоторые из них, как наиболее понятные и эффективные в своем исполнении.

1. Представление. Для начала можно просто представлять в своем воображении различные предметы, чаще всего линии и геометрические фигуры, и пытаться их передвигать, поворачивать, крутить.

2. Копирование. Такого вида упражнение с усложнением, требует чуть больше времени. Необходимо сперва изобразить небольшой предмет на листе, после чего чуть увеличить изображение в размере. Нарисовать с дополнительным предметом рядом, и в объемном виде.

3. Чертежи и схемы. Выберете ограниченное пространство или объемный предмет и создайте чертёж.

4. Графические тренажеры. Они позволяют обогащать свои навыки каждый раз новыми приемами. Их с легкостью можно найти в Интернете.

Например:

1)       Восстановить элемент фигуры (симметрия)(рис.1)

 

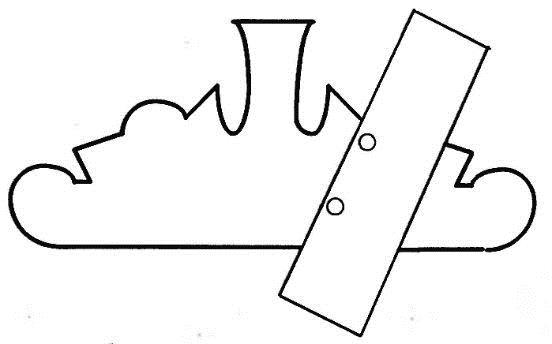
Рис.1

  

2)       Кто быстрее доберется до выхода? (если представить, что круги – это люди)(рис.2)

 

 

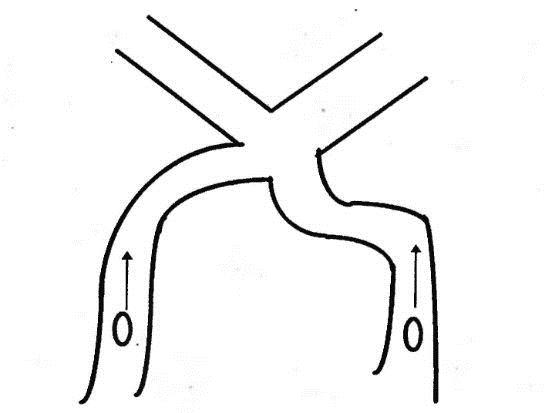
Рис.2

 

3)       Куда упадет шарик?(рис.3)

 

Рис.3

 

4)       Какие фигуры пройдут между фигурами А и Б? (рис.4)

 

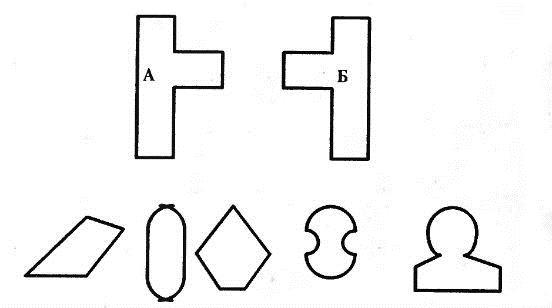
Рис.4

  

5)       На какой отметке должен оказаться человек, чтобы на него не упало дерево? (рис.5)

 

Рис.5

 

Заключение

И в заключение можно сказать, что начать заниматься развитием математических представлений никогда не поздно, необходимо лишь захотеть. Ведь математика это не просто наука, это значительная часть нашей жизни. Она способствует успехам в учебе, работе, человек привыкает разбивать сложные задачи на более мелкие, сохранять в голове большое количество информации и оперировать ей, справляться с трудностями, выявлять взаимосвязи событий. Причем все это может пригодиться как в математике, так и в любой другой науке.

1. Ядловский А. Тренажер для развития математических способностей. – М., ACT, 2016. –64 с.
2. Кузнецова В.Г. Математика для дошкольников. Популярная методика игровых уроков. – СПб.: Оникс, 2000.
3. Являются ли математические способности врождёнными. URL: https://newtonew.com/science/math-ability-innate (дата обращения: 21.04.2019).
4. Что такое математические способности и как их развить URL: https://jkpersyblog.com/chto-takoe-matematicheskie-sposobnosti-i-kak-ih-razvit (дата обращения: 21.04.2019).
5. Как развивать математический склад ума? URL: http://reshit.ru/kak-razvivat-matematicheskij-sklad-uma (дата обращения: 21.04.2019).

Рецензии:

4.05.2019, 17:26 Мирмович Эдуард Григорьевич
Рецензия: Представленная для публикации статья структурирована, освоена технология включения иллюстраций, сделана попытка (пусть не очень удачная) сформулировать актуальность, научную новизну и др. Всё это говорит о потенциальной возможности авторов публикации статей в данном электронном журнале. Однако текст статьи не отвечает своему обобщённому и претенциозному названию. Приведены лишь несколько упрощённых тестов, принадлежащих не самим авторам. Классификация математического мышления на приведенных 5 типов принадлежит лишь одному учёному из Новгородского филиала Академии народного хозяйства Илье Яковлевичу Каплуновичу ("Развитие пространственного мышления школьников в процессе обучения математике – Новгород: МО РФ, 1996), кстати, кандидату психологических наук. Никто из признанных математиков данную, искусственную дифференциацию признаков математического мышления не подтвердил. Но это не главное. Главное, что уровень проработки выраженной цели на столько не глубок, что авторы и руководители не нашли нужным сослаться на автора этой классификации. Кроме того, приведенные примеры, претендующие на "Методику развития математического мышления", никакого отношения к этой классификации не имеют. Математическое мышление (ММ) является одним из направлений словесно-логического типа мышления. Истинными признаками наличия ММ у человека являются логическая предопределённость рассуждений (доказательность от аксиом до теорем), лаконизм и строгость, аналитичность, склонность к компактности и символике в изложении умозаключений. Отсутствует УДК. В работе допущено огромное число грамматических и синтаксических ошибок. В представленном виде рецензент не может дать положительный отзыв для публикации этой статьи в данном журнале, что не отвергает... читай начало рецензии.



Комментарии пользователей:

5.05.2019, 16:18 Рукавишникова Екатерина Леонидовна Отзыв: 5.05.2019 Рукавишникова Екатерина Леонидовна. ОТЗЫВ: Не осмелилась писать рецензию, так как с математикой на Вы. К автору Кудриной Анне Игоревне есть вопросы по логике изложения и желание помочь это исправить. 1. Не нужно проводить границу между людьми, которые занимаются творчеством и теми, кто любит математику. Давида Гильберта (1862-1943) спросили об одном из его бывших учеников. - Ах, этот-то? - вспомнил Гильберт. - Он стал поэтом. Для математики у него было слишком мало воображения.2. Актуальность прописана невнятно. ...этого вопроса. Какого? 3. В абзаце со слов СПЕРВА какая-то мешанина. Несколько тем в нескольких предложениях :умение работать с цифрами; талант и его наличие; математические операции производимые на калькуляторе или в уме; специалист, который может упростить любую сложную задачу. Воспользуйтесь логикой изложения материала по формуле- Т-А-В. Тезис-Аргумент-Вывод. 4. Затем появляется новая тема -Математическое мышление и его типы. В конце- Математическое представление. Необходимо развести все эти понятия, либо не использовать их как синонимы СПОСОБНОСТЕЙ. Статью необходимо доработать.

Оставить комментарий