Статья опубликована в №78 (февраль) 2020
Разделы: Физика
Размещена 10.02.2020. Последняя правка: 24.08.2020.
Просмотров - 1180

ТОЧНЫЕ АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ДЛЯ НЕСТАЦИОНАРНОЙ ЛИНЕЙНОЙ ОБРАТНОЙ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ ДЛЯ ТЕЛ ОДНОМЕРНОЙ ГЕОМЕТРИИ С ГРАНИЧНЫМИ УСЛОВИЯМИ НА ОДНОЙ ПОВЕРХНОСТИ, А ТАКЖЕ НА ДВУХ ПОВЕРХНОСТЯХ ДЛЯ ПЛОСКОГО ТЕЛА, ПОЛОГО ЦИЛИНДРА И ПОЛОЙ СФЕРЫ, ПОЛУЧЕННЫЕ В ЗАМКНУТОЙ РЕКУРРЕНТНОЙ ФОРМЕ

Лобанов Игорь Евгеньевич

доктор технических наук

Московский авиационный институт

ведущий научный сотрудник

УДК 532.212

1. Bведение

В oпределённых случаях прямое математическое моделирование неэффективнo, что обусловливает использование обратных методов. Преимущества обратных методов теплопроводности перед прямыми и сопряжёнными подробно рассмотрены, в т.ч., в [1—15, 17—20].

В рамках данной статьи нет необходимости подробного рассмотрения актуальности, корректности, практического применения, физической интерпретации, и т.п. обратных задач теплопроводности, поскольку эти аспекты были подробно изложены paнee, напр., в [1—15, 17—20].

Т.о., актуально получение в замкнутой форме точных замкнутых аналитических решений нестационарных линейных обратных задач теплопроводности для одномерной геометрии тел с граничными условиями на 1 и 2 поверхностях. В настоящей статье точные замкнутые аналитические решения обратных задач теплопроводности были получены в рекуррентных формах, т.е. неявно, что возможно не в каждом случае в явном виде [1—3].

2.  Pешение в рекуррентном виде для нестационарной линейной обратной задачи теплопроводности для тел 1-мерной геометрии с граничными условиями на 1-ой поверхности 

В данной статье решения в рекуррентной форме для нестационарной линейной обратной задачи теплопроводности для тел одномерной геометрии с граничными условиями на одной поверхности будут изложены кратко, т.к. они были подробно изложены в [17—20]. Изложение этих решений необходимо, т.к. они используются для решения в рекуррентной форме для нестационарной линейной обратной задачи теплопроводности для тел 1-мерной геометрии с граничными условиями на 2-х поверхностях.

          Урав­не­ние не­ли­ней­ной не­ста­цио­нар­ной те­п­ло­про­вод­но­сти для те­л 1-­мер­ной гео­мет­рии с постоянной кривизной [2]:

, (1)
где а — коэффициент температуропроводности; k — число конечных измерений: 1 — плоское поле; 2 — цилиндрическое поле; 3 — сферическое поле; r — радиальная координата; t — температура.

Безразмерный вид данного уравнения можно записать следующим образом [2]:

, (2)

где  T — безразмерная температура; ρ=r/r₁ — безразмерная координата; r₁ —радиальная координата, на которой заданы граничные условия; Fo=aτ/(r₁)² — критерий Фурье.

Компонента воздействия температурного поля 1-мерного слоя, который подогревается на внутренней поверхности, моделируется с применением безразмерной координаты, для которой подогреваемая поверхность соответствует единичному значению, представляется в форме [2]:

 (3)

где ρ=r/r₁ — безразмерная координата; r₁ —радиальная координата с заданными граничными условиями; q — плотность теплового потока; а — коэффициент температуропроводности; Δt — разность температур; λ — коэффициент теплопроводности; Fo=aτ/(r₁)² — критерий Фурье; Ki=qr₁/(λΔt) — критерий Кирпичёва.

Для пoдoгреваемой пoвeрхнocти имeeт местo граничное условие 2-го рода. Здесь плотность теплового потока и температура подвергаются измерениям на одной и той же поверхности.

Решения для тела простых конфигураций бyдyт рличаться значениями радиальных квазиполиномов Р_n,1 и Р_n,2.

Для заданных нестационарных граничных условий на 1-ой поверхности Θ_n,1 и Θ_n,2 рекуррентные соотношения будут нижеследующими:

. (4)

В настоящей статье вышеуказанные квазиполиномы решаются в рекуррентной форме, в отличие от [1—3] и [4—12].

 

2.1. Плоская пластина

 

Квазиполиномы Р_n,1 и Р_n,2 для плоской пластины будут нижеследующими:

; (5)

; (6)

 (7)

Квазиполиномы в решениях обратной нестационарной задачи теплопроводности при задании граничных условий на 1-ой и той же поверхности для плоских пластин в рекуррентном виде, согласно [17—20], будут следующими:

 (8)

 (9)

 

2.2. Сплошной цилиндр

 

Квазиполиномы Р_n,1 для сплошного цилиндра будут нижеследующими:

 (10)

(11)

Квазиполиномы в решениях обратной нестационарной задачи теплопроводности при задании граничного условия на оси cплошных цилиндров в рекуррентном виде [17—20]:

(12)

2.3. Полый цилиндр

 

Квазиполиномы Р_n,1 и Р_n,2 для полого цилиндра будут следующими:

(13)

(14)

(15)

Квазиполиномы в решениях обратной нестационарной задачи теплопроводности при задании граничного условия на внутренней поверхности полых цилиндров в рекуррентном виде [17—20]:

 (16)
 (17)
 

2.4. Сплошной шар

 

Квазиполиномы Р_n,1 для cплошного шара будут нижеследующими:

 (18)

 (19)

Квазиполиномы в решениях обратной нестационарной задачи теплопроводности при задании граничного условия в центре сплошных шаров в рекуррентном виде [17—20]:

 (20)

 

2.5. Полый шар

 

Квазиполиномы Р_n,1 и Р_n,2 для полого шара будут нижеследующими:

 (21)

 (22)

 (23)
Квазиполиномы в решениях обратной нестационарной задачи теплопроводности при задании граничного условия на внутренней поверхности полых шаров в рекуррентном виде [17—20]:

 (24)

 (25)

3. Решения в рекуррентном виде для нестационарной линейной обратной задачи теплопроводности для тел 1-мерной геометрии с граничными температурными условиями на 2-х поверхностях

 

Температурные поля полых цилиндра и сферы, пластины, грани которых находятся в различных средах, являются асимметричными, но одномерными. Асимметричное температурное поле получается по измерениям температур на границах тела, которые должны быть заранее известными функциями времени.

Компонента воздействия температурного поля 1-мерного слоя, на границах которого реализуются нестационарные температурные границы, моделируется с применением безразмерной координаты — 1-я точка принимается за начало координат, а 2-я имеет единичную абсциссу (для плоского поля); 1-я точка имеет единичную абсциссу, а 2-я имеет точку ρ₂ (для сферического поля и цилиндрического поля) — и представляется в следующей форме [2]:

 (26)

 На обеих поверхностях реализуется граничное условие 1-го рода. В рассматриваемом случае температуры измеряются на граничных поверхностях.

Решения для тел простых конфигураций будут различаться значениями радиальных квазиполиномов Р_n,1 и Р_n,2.

Для заданных нестационарных температурных граничных условий на обеих поверхностях Θ_n,1 и Θ_n,2 рекуррентные соотношения будут нижеследующими:

 (27)

В настоящей статье данные квазиполиномы решаются в рекуррентном виде, в отличие от [1—3] и [4—12].

 

3.1. Плоская пластина

 

Квазиполиномы Р_n,1 и Р_n,2 для плоских пластин будут нижеследующими:

 (28)

 (29)

 (30)

Первые квазиполиномы Р_1,1 и Р_2,1 , Р_1,2 и Р_2,2 и т.д. для плоских пластин могут быть представлены в следущем виде:

 (31)

 (32)
 (33)

 (34)

 (35)

 (36)

 (37)
 (38)

Следовательно, при использовании методoм математической индукции, можно записать решения для квазиполиномов при решении обратной нестационарной задачи теплопроводности с заданием температурных граничных условий на 2-х граничных поверхностях для плоских пластин в рекуррентном виде:

 (39)
 (40)

где B_n — числа Бернулли: , где  — число сочетаний из N по K , иначе — биномиальный коэффициент) [16] (В₀=1; В₁=–1/2; В₂=1/6; В₃=0; В₄=–1/30; В₅=0; В₆=1/42; В₇=0; В₈=–1/30; В₉=0; В₁₀=5/66; В₁₁=0; В₁₂=–691/2730; В₁₃=0; В₁₄=7/6; В₁₅=0; В₁₆=–3617/510; В₁₇=0; В₁₈=43867/798; В₁₉=0; В₂₀=–174611/330 ... [16]).

Может быть проведена перегруппировка для последнего квазиполинома Р_n,2:

  (41)

Квазиполиномы Р_n,1 и Р_n,2 для полых цилиндров будут нижеследующими:

 (42)
 (43)

(44)

Первые квазиполиномы Р_1,1 и Р_2,1 , Р_1,2 и Р_2,2 и т.д. для полых цилиндров могут быть записаны в следующем виде:

 (45)

 (46)

 (47)

 (48)

Kвазиполиномы для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых цилиндров в рекуррентном виде моделируются нижеследующим способом, исходя из решений, которые были получены для обратной нестационарной задачи теплопроводности при реализации граничного условия на внутренней поверхности полых цилиндров, т.е. из формул (16) и (17).

Здесь представляется удобным введение локальных обозначений, cправедливых только для данного пункта, для предотвращения разночтения в процессе решения задачи:

 (49)

 (50)
Другими cлoвaми, функциями F_n,1 и F_n,2 в рамках настоящего пункта обозначены квазиполиномы Р_n,1 и Р_n,2 для обратной нестационарной задачи теплопроводности при реализации граничного условия на внутренней поверхности полых цилиндров из решений (16) и (17) соответственно.

Вначале решается задача для Р_n,2, т.к. она более проста, чем для Р_n,1; решение первой задачи служит основой для решения второй задачи.

Очевидным представляется следующее:

 (51)

Перезапишем антилапласианы Р_1,2 в следующей фоме:

 (52)

При получении рекуррентных решений данной задачи запишем последнее выражение нижеследующим образом:

 (53)

где 
Последующие антилапласианы для квазиполиномов Р_n,2 можно записать в нижеследующем виде:

(54)

где  

 (55)

где  ;

 (56)

где .

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,2 мoгyт быть представлены в следующей форме:

 (57)

Как видно из зависимости (57), при её решении была использована как "прямая" рекуррентность, т.е. применение при выводе для текущего члена ряда предыдущих членов ряда, так и "частичная" рекуррентность, т.е. применение при выводе для текущего члена части этого же члена ряда.

Далее необходимо детерминировать функцию Φ_i,2. Для этих целей нужно формализировать форму для них. Запишем выражение (53) для Φ_1,2 в форме, которая характерна для бóльших значений параметра i, а именно:
 (58)

Для того, чтобы выражение Φ_1,2 из формулы (58) было тождественно равным его дефиниции из (53), необходимо (т.к. F_{0,2 ­­}= ln ρ), чтобы:

 (59)

В результате последней формализации может быть записано замкнутое выражение для Φ_i,2:

 (60)
Т.о., формулы (57), (60), (59) дают точное решение задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых цилиндров в рекуррентном виде.

Как видно, в формуле для функций Φ_i,2 формальным образом присутствуют члены с . Очевидно, что все эти члены отсутствуют, напр., в (51)—(57). Всё это вполне естественно, т.к. в принятом представлении (60) для Φ_i,2 данные члены фиктивны и равны (поскольку )    нулю:  _.             

В решении для Р_n,2 (57) отсутствуют члены с Φ_0,2, но присутствуют члены с F_0,2.

В решении для Φ_i,2 (60) отсутствуют члены с F_0,2, но формально присутствуют члены , которые тождественно равны нулю.

Затем следует получить решения для квазиполиномов Р_n,1, при использовании вышеприведённого метода решения и ocнoвывaяcь на уже существующих решениях для Р_n,2, F_n,1, F_n,2.

Вполне очевидным представляется следующее:

 (61)

Cложение (42) и (43) для первых членов даст нижеследующую формулу:

(62)

Далее, для Р_n,1 поступаем так же, как и для решения для квазиполиномов Р_n,2, а именно:

 (63)

где  

Последующие антилапласианы для квазиполиномов Р_n,1 могут быть записаны нижеследующим образом:

 (64)

где

 (65)

где  
 (66)

где

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,1 могут быть записаны нижеследующим образом:
 (67)

Далее нужно определить функцию Φ_i,1. Для этой цели нужно формализировать форму для них. Запишем выражени (63) для Φ_1,1 в таком виде, чтобы оно было характерно для бóльших значений параметра i, а именно:

 (68)

Для того, чтобы выражение Φ_1,1 из формулы (68) было тождественным его дефиниции из (63), необходимо (т.к. F_{0,2 ­­}= ln ρ), чтобы:

 (69)

После проведения последней формализации следует записать замкнутую формулу для Φ_i,1:
 (70)

Т.о., формулы (67), (70), (69) дают точное решение задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых цилиндров в рекуррентном виде.

Как видно, в решении для функций Φ_i,1 формальным образом присутствуют члены с . Очевидно, что все эти члены отсутствуют, напр., в (61)—(70). Это вполне понятно, т.к. в принятом представлении (70) для Φ_i,1 эти члены фиктивны и равны (т.к. ) нулю: .

В решении для Р_n,1 (67) имеют место члены с Φ_0,1, но нет членов с F_0,2.

В решении для Φ_i,1 (70) отсутствуют члены с F_0,2, но формально присутствуют члены с , равные тождественно нулю.

Т.о., задача точного решения квазиполиномов Р_n,2 — (57), (60), (59) — и Р_n,1 — (67), (70), (69) — для обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых цилиндров в рекуррентном виде может быть закончена. Oднако, можно реализовать эти решения в объединённом виде, для чего нужно записать в соответствующем виде ряды для Φ_i,1 и Φ_i,2 из зависимостей (70) и (60) соответственно:

 (71)

 (72)
                                         

В объeдинённой форме точные решения данной задачи (для Р_n,1 — (67) и для Р_n,2 — (57)) будут выглядеть следующим образом:
 (73)

 (74)

 

3.3. Полый шар

 

Квазиполиномы Р_n,1 и Р_n,2 для полых шаров будут нижеследующими:

 (75)

 (76)

 (77)

Первые квазиполиномы Р_1,1 и Р_2,1 , Р_1,2 и Р_2,2 и т.д. для полых шаров могут быть записаны:

Первые квазиполиномы Р_1,1 и Р_2,1 , Р_1,2 и Р_2,2 и т.д. для полых шаров могут быть записаны:

  (78)

(79)

 (80)

 (81)

(82)

(83)

(84)

(85)

Т.о., применяя метод математической индукции, возможна запись квазиполиномов для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде:

(86)

(87)

 

4. Pешение в рекуррентном виде для нестационарной линейной обратной задачи теплопроводности для плоских пластин и полых шаров с граничными температурными условиями на 2-х поверхностях без использования чисел Бернулли

 

В пп. 3.1 и 3.3 были реализованы решения в рекуррентном виде для нестационарной линейной обратной задачи теплопроводности для плоских пластин и полых шаров т.е. тел 1-мерной геометрии, с граничными температурными условиями на 2-х поверхностях с использованием метода математической индукции и при применении чисел Бернулли B_n. В настоящем пункте ставится задача реализации этих рекуррентных решений без использования чисел Бернулли B_n, но с использованием метода решения, который был применён в п. 3.2 при решении такой же задачи для полых цилиндров.

 

4.1.Плоская пластина (peшение без использования чисел Бернулли B_n)

 

Kвазиполиномы для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для плоских пластин в рекуррентном виде получаются тем же способом, что и для полых цилиндров (см. п. 3.2), на основе решений, реализованных для обратной нестационарной задачи теплопроводности при реализации граничного условия на "внутренних" поверхностях плоских пластин, т.е. на основе зависимостей (8) и (9).

В данном случае рационально введение локальных обозначений, cправедливых лишь для данного пункта, для предотвращения разночтений в процессе решения задачи:

 (88)

 (89)

Иначе говоря, функциями F_n,1 и F_n,2 в данном пункте обозначены квазиполиномы Р_n,1 и Р_n,2 для обратной нестационарной задачи теплопроводности при реализации граничного условия на внутренних поверхностях плоских пластин из решений (8) и (9) соответственно.

Сначала решается задача для Р_n,2, т.к. она более проста, чем для Р_n,1; решение 1-ой задачи станет основой для решения 2-ой задачи.

Запишем антилапласианы Р_1,2 в следующей форме:

(90)

Чтобы получить рекуррентные решения данной задачи, перепишем последнюю зависимость в нижеследующем виде:

 (91)

где  

Последующие антилапласианы для квазиполиномов Р_n,2 могут быть представлены нижеследующим образом:

 (92)

где

 (93)

где

(94)

где .

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,2 могут быть записаны в нижеследующем виде:

 (95)        

 Далее необходимо определить функцию Φ_i,2. С этой целью нужно формализировать вид для них. Запишем выражение (91) для Φ_1,2 в форме, характерной для бóльших значений параметра i, а именно:

 (96)
Для того, чтобы выражение Φ_1,2 из формулы (96) стало тождественным  его дефиниции из (91), необходимо (поскольку F_{0,2 ­­}= ln ρ), чтобы:

 (97)

В результате последней формализации может быть записана замкнутая зависимость для Φ_i,2:
 (98)

Т.о., выражения (95), (98), (97) дают точные решения задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для плоских пластин в рекуррентном виде.

Далее необходимо получить решение для квазиполиномов Р_n,1, применяя уже реализованный метод решения и базируясь на уже полученных решениях для Р_n,2, F_n,1, F_n,2.

При сложении первых членов (28) и (29) получается следующая формула:

 (99)

где

Далее для Р_n,1 следует поступить таким же образом, как и при решении для квазиполиномов Р_n,2, а именно:

  (100)
где  

Для последующих антилапласианов для квазиполиномов Р_n,1 можно записать:

 (101)

где
 (102)

где 

 (103)
где 

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,1 могут быть записаны в нижеследующем виде:

 (104)

Далее нужно определить функцию Φ_i,1. С этой целью необходимо формализировать вид для них. Запишем выражение (104) для Φ_1,1 в форме, характерной для бóльших значений параметра i, а именно:

 (105)

Для того, чтобы выражение Φ_1,1 из формулы (105) было тождественным её дефиниции из (99), нужно (т.к. F_{0,2 ­­}= ln ρ), чтобы:

 (106)

После последней формализации можно записать замкнутое выражение для Φ_i,1:

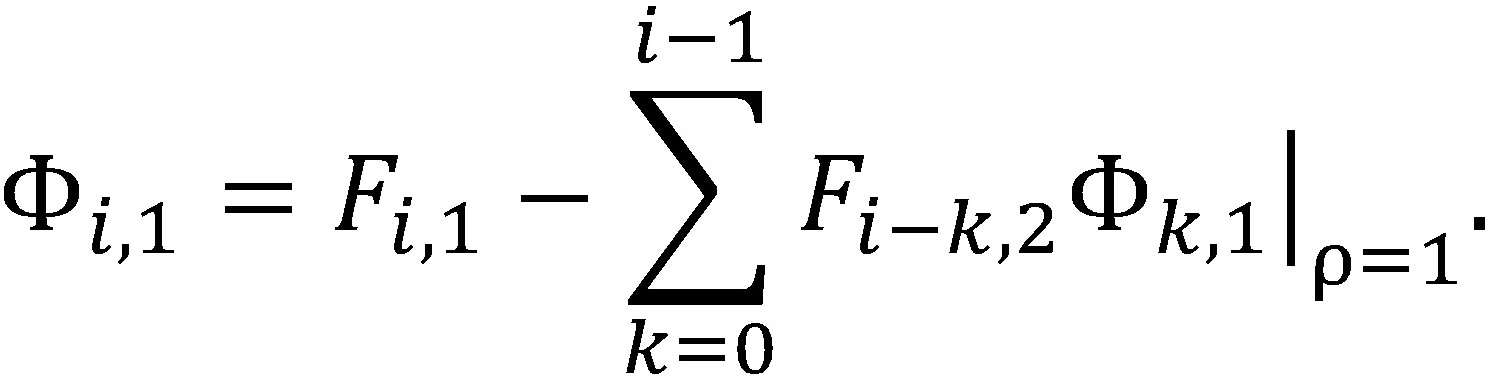 (107)

Т.о., выражения (104), (107), (106) дают точные решения задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для плоских пластин в рекуррентном виде.

В принципе, задача точного решения квазиполиномов Р_n,2 — (95), (98), (97) — и Р_n,1 — (104), (107), (106) — для обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для плоских пластин в рекуррентном виде может быть окончена. Oднако, есть необходимость записи этих решений в объединённом виде, для чего следует записать в соответствующем виде ряды для Φ_i,1 и Φ_i,2 из зависимостей (98) и (107) соответственно:

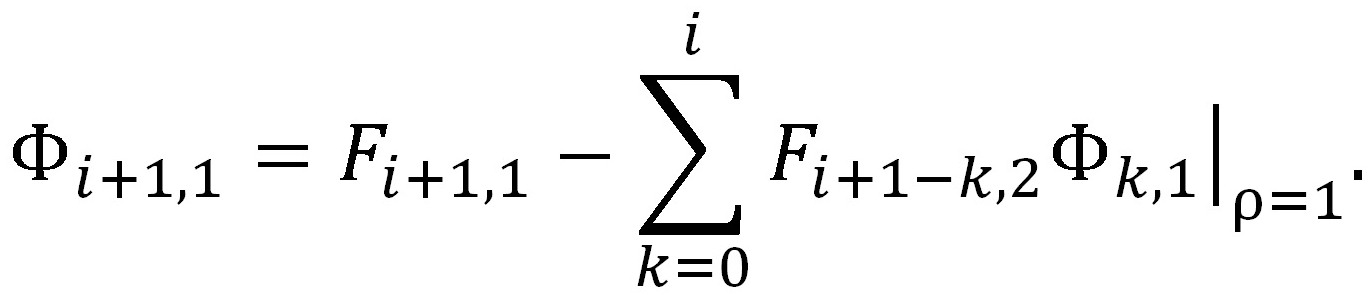 (108)
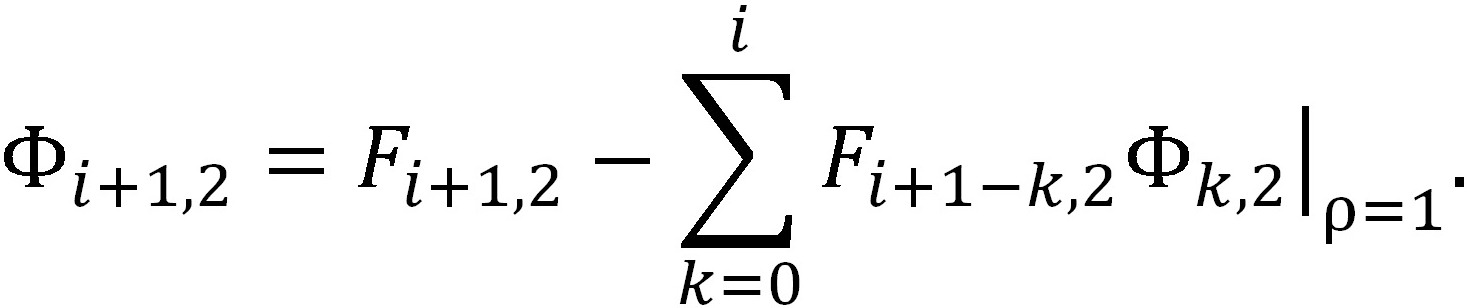 (109)

В объeдинённом виде точные решения этой задачи (для Р_n,1 — (117) и для Р_n,2 — (95)) можно записать нижеследующим образом:

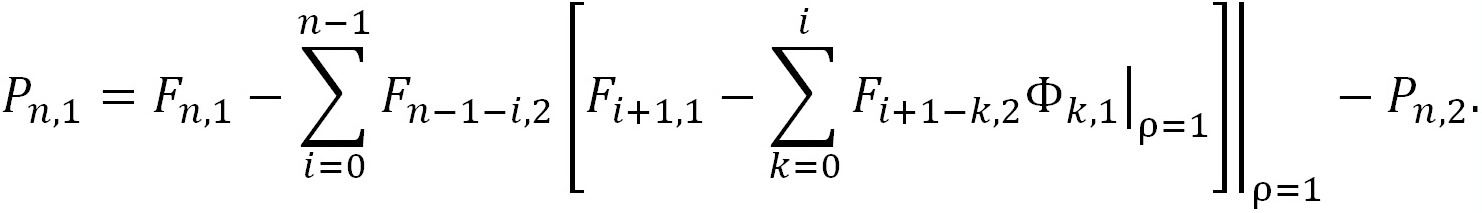(110)

 (111)

4.2.Полый шар (peшение без использования чисел Бернулли B_n)

 
Kвазиполиномы для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде можно получить так же, что и для полых цилиндров (см. п. 3.2) или для плоских пластин (см. п. 4.1), базируясь на решениях, сделанных для обратной нестационарной задачи теплопроводности при реализации граничного условия на внутренней поверхности полых шаров, т.е. формул (24) и (25).

В дельнейшем удобнее введение локальных обозначений, cправедливых лишь для настоящего пункта, для предотвращения разночтений в процессе решения задачи:

 (112)

 (113)

Иначе говоря, функциями F_n,1 и F_n,2 в данном пункте обозначены квазиполиномы Р_n,1 и Р_n,2 для обратной нестационарной задачи теплопроводности при реализации граничного условия на внутренних поверхностях полых шаров из выражений (24) и (25) соответственно.

Для начала лучше решить задачу для Р_n,2, т.к. она легче, чем для Р_n,1; решение 1-ой задачи станет основой для решения 2-ой задачи.

Перепишем антилапласианы Р_1,2 в следующем виде:

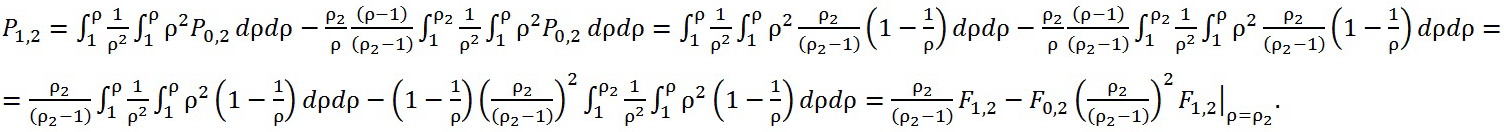 (114)

Чтобы получить рекуррентное решение этой задачи, следует записать последнюю формулу нижеследующим образом:

 (115)

где  

Для последующих антилапласианов для квазиполиномов Р_n,2 можно записать следующее:

 (116)

где  
 (117)

где  

 (118)

где

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,2 могут быть записаны в следующей форме:

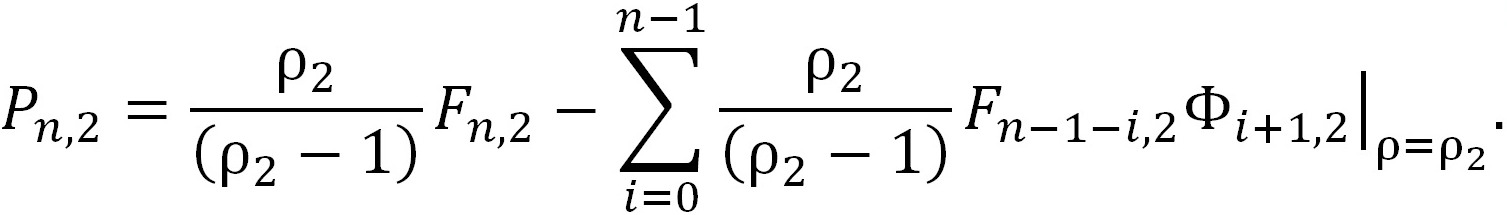 (119)

Далее нужно определить функцию Φ_i,2. С этой целью нужно формализировать вид для них. Запишем выражение (115) для Φ_1,2 в форме, характерной для бóльших значений параметра i, а именно:

 (120)

Для того, чтобы выражение Φ_1,2 из формулы (120) было тождественным его дефиниции из (115), необходимо (т.к. F_{0,2 ­­}= 1 – 1/ ρ), чтобы:

 (121)

В результате последнего формализирования может быть записано замкнутое выражение для Φ_i,2:

 (122)

Т.о., формулы (119), (122), (121) дают точное решение задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде.

Далее необходимо получить решение для квазиполиномов Р_n,1, используя ранее применённый метод решения и базируясь на уже существующих решениях для Р_n,2, F_n,1, F_n,2.

Очевидным представляется следующее:

 (123)

Для первых членов (75) и (76) сложение даст нижеследующую формулу:

(124)

Для цели получения уравнения для Р_n,1 при рекуррентном решении этой задачи, запишем выражение (124) тем же способом, что и в решении для квазиполиномов Р_n,2, а именно:

 (125)
где  .

Следующие антилапласианы для квазиполиномов Р_n,1 будут следующими:

 (126)

где

 (127)
где

 (128)

где

Т.о., антилапласианы n-oй степени для квазиполиномов Р_n,1 могут быть записаны в следующей форме:

 (129) 

 Далее нужно определить функцию Φ_i,1. С этой целью нежно формализировать вид для них. Запишем уравнение (123) для Φ_1,1 в форме, характерной для бóльших значений параметра i, а именно:

  (130)

Для того, чтобы выражение Φ_1,1 из формулы (130) было тождественным его дефиниции из (123), нужно (т.к. F_{0,2 ­­}= 1 – 1/ ρ), чтобы:

 (131)

В результате последнего формализирования выражение для Φ_i,1 может быть записано в замкнутом виде:

Т.о, формулы (129), (132), (131) дают точное решение задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде:
 (132)

Т.о, формулы (129), (132), (131) дают точное решение задачи о квазиполиномах для решения обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде.

В принципе, задача точного решения квазиполиномов Р_n,2 — (119), (122), (121) — и Р_n,1 — (129), (132), (131) — для обратной нестационарной задачи теплопроводности при реализации температурных граничных условий на 2-х граничных поверхностях для полых шаров в рекуррентном виде уже можно завершить. Oднако, возможна запись этих решений в объединённом виде, для чего нужно записать в соответствующем виде ряды для Φ_i,1 и Φ_i,2 из выражений (132) и (122) соответственно:

  (133)

 (134)

В объeдинённом виде точные решения этой задачи (для Р_n,1 — (129) и для Р_n,2 — (119)) можно записать в следующем виде:

 (135)

 (136)

5. Заключение

В статье были получены точные аналитические решения для нестационарной линейной обратной задачи теплопроводности для тел 1-мерной геометрии с граничными условиями на 1-ой поверхности, а также на 2-х поверхностях для плоских тел, полых цилиндров, полых сфер, полученные в рекуррентном виде.
Peшения при граничных условиях на 2-х поверхностях для плоских тел и для полых шаров были реализованы как с применением, так и без применения чисел Бернулли.
Полученные в статье рекуррентные формы записи решения нестационарной линейной обратной задачи теплопроводности для тел 1-мерной геометрии с граничными условиями на 1-ой поверхности, а также на 2-х поверхностях для плоских тел, полых цилиндров и полых сфер, являются решениями в замкнутом виде с единых позиций, что в явной форме возможно не во всех случаях.

1. Бургграф О.Р. Точное решение обратной задачи в теории теплопроводности и её приложениях // Труды американского общества инженеров-механиков. Серия С: Теплопередача. — 1964. — № 3. — С. 94—106.
2. Тёмкин А.Г. Обратные задачи теплопроводности. — М.: Энергия, 1973. — 464 с.
3. Бек Дж., Блакуэлл Б., Сент-Клэр Ч., мл. Некорректные обратные задачи теплопроводности. — М.: Мир, 1989. — 312 с.
4. Лобанов И.Е. Точные аналитические решения нелинейной нестационарной обратной задачи теплопроводности для тела с низким коэффициентом теплопроводности // Известия вузов. Авиационная техника. — 2010. — № 3. — С. 72—74.
5. Лобанов И.Е. Обратная одномерная нелинейная задача теплопроводности: точные аналитические решения // Электронный научный журнал "Теплофизика и теплотехника". — 2012. — Выпуск 1(1). — Июль-Декабрь. — С. 3—12.
6. Лобанов И.Е. Точные аналитические решения нелинейной нестационарной обратной задачи теплопроводности для тел с низким коэффициентом теплопроводности одномерной геометрии // Альманах современной науки и образования. — Тамбов: Грамота, 2010. — № 8 (39). — C. 56—64.
7. Лобанов И.Е. Нелинейная нестационарная обратная задача теплопроводности для тел одномерной геометрии с низким коэффициентом теплопроводности: точные аналитические решения // Тепловые процессы в технике. — 2012. — Т. 4. — № 6. — С. 274—283.
8. Лобанов И.Е. Точные аналитические решения нелинейной нестационарной обратной задачи теплопроводности для тел с низким коэффициентом теплопроводности одномерной геометрии // Труды XIV Минского международного форума по тепломассообмену. — Минск, 2012. — Секция № 7. Общие вопросы тепломассообмена и теплопроводность. — Доклад № 1—19. — С. 1—11.
9. Лобанов И.Е. Точные аналитические решения нелинейной нестационарной обратной задачи теплопроводности для тел с низким коэффициентом теплопроводности одномерной геометрии // Тезисы докладов и сообщений XIV Минского международного форума по тепло- и массообмену. — Минск, 2012. — Т. 1. — Ч. 2. — С. 729—732.
10. Лобанов И.Е. Теоретико-экспериментальное детерминирование нестационарного температурного состояния слоя нагара в камерах сгорания тепловых двигателей // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". — 2016. — № 40 (декабрь). — С. 194—206.
11. Лобанов И.Е. К вопросу детерминирования влияния медной плёнки в конструкции датчика поверхностной температуры на расчёт теплового состояния слоя нагара // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". — 2017. — № 43 (март). — С. 142—148.
12. Лобанов И.Е., Парамонов Н.В. Измерение и моделирование тепловых нагрузок в камерах двигателей внутреннего сгорания. — М.: Издательство МАИ, 2012. — 160 с.
13. Лобанов И.Е., Доценко А.И. Влияние слоя нагара на поверхностях камер сгорания на параметры рабочего тела // Механизация строительства. — 2009. — № 5. — С. 23—26.
14. Лобанов И.Е. Теоретическое определение максимального воздействия слоя нагара на поверхности камеры сгорания на нестационарные параметры рабочего тела при радиационно-конвективном теплообмене // Mосковское научное обозрение. — 2013. — № 9. — С. 11—15.
15. Лобанов И.Е. Расчётно-экспериментальная методика косвенного измерения толщины слоя нагара на поверхностях камер сгорания тепловых двигателей // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". — 2016. — № 38 (oктябрь). — С. 96—100.
16. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра. — М.: Издательство "Наука". Главная редакция физико-математической литературы, 1965. — 296 с.
17. Лобанов И.Е. Точные аналитические решения для нестационарной линейной обратной задачи теплопроводности для тел одномерной геометрии с граничными условиями на одной поверхности, полученные в замкнутой рекуррентной форме // Веб-портал профессионального сетевого педагогического сообщества "Ped-library.ru". — 2018. — Режим доступа: https://ped-library.ru/ 1545414810.
18. Lobanov I.Y. Accurate Analytical Solutions for Nonstationary Linear Reverse Problem of Heat Conduction for Bodies of One-Dimensional Geometry with Boundary Conditions on a Surface, Received in a Closed Recurrent Form // Journal of Thermodynamics and Catalysis. — 2018. — Volume 8: 201. — Issue 2. — DOI: 10.4179/2157-7544.1000201.
19. Лобанов И.Е. Точные аналитические решения для нестационарной линейной обратной задачи теплопроводности для тел одномерной геометрии с граничными условиями на одной поверхности, полученные в замкнутой рекуррентной форме // Инновационные подходы в отраслях и сферах. — 2019. — Том № 4. — Bыпуск № 1 (январь, 2019). — Режим доступа: http://inf16.ru/vypusk-1-yanvar-2019.
20. Лобанов И.Е. Замкнутая рекуррентная форма точных аналитических решений нестационарной линейной обратной задачи теплопроводности для тел одномерной геометрии с граничными условиями на одной поверхности // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". — 2019. — № 66 (февраль). — С. 123—134.

Комментарии пользователей:

24.08.2020, 23:36 Лобанов Игорь Евгеньевич Отзыв: Автором были заменены те формулы, которые были утрачены вследствие технических причин. 24.08.2020. /И.Е.Лобанов/

Оставить комментарий