- » Антропология
- » Археология
- » Архитектура
- » Астрономия
- » Библиотековедение
- » Биология
- » Биотехнологии
- » Ботаника
- » Ветеринария
- » Военные науки
- » География
- » Геология
- » Журналистика
- » За горизонтом современной науки
- » Зоология
- » Информационные технологии
- » Искусствоведение
- » История
- » Культурология
- » Лингвистика
- » Литература
- » Маркетинг
- » Математика
- » Машиностроение
- » Медицина
- » Менеджмент
- » Методика преподавания
- » Музыковедение
- » Нанотехнологии
- » Науки о Земле
- » Образование
- » Оптика
- » Педагогика
- » Политология
- » Правоведение
- » Психология
- » Регионоведение
- » Религиоведение
- » Сельское хозяйство
- » Социология
- » Спорт
- » Строительство
- » Телекоммуникации
- » Техника
- » Туризм
- » Управление и организация
- » Управление инновациями
- » Фармацевтика
- » Физика
- » Физическая культура
- » Филология
- » Философия
- » Химия
- » Экология
- » Экономика
- » Электроника
- » Электротехника
- » Юриспруденция
Феномен наногерцовых гравитационных волн
УРАВНЕНИЕ СОСТОЯНИЯ ПРОДУКТОВ ДЕТОНАЦИИ ОКТОГЕНА ИЗ ЭКСПЕРИМЕНТА И ИЗ ТЕРМОХИМИЧЕСКОГО РАСЧЕТА
Гипотеза о возможности образования больших галактик уже в ранней Вселенной
Рассуждения о быстрых гамма-всплесках «космических струн» Стивена Хокинга
Разделы: Физика
Размещена 30.09.2020. Последняя правка: 15.10.2020.
Просмотров - 1133
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИНТЕНСИФИЦИРОВАННОГО ТЕПЛООБМЕНА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ПОПЕРЕЧНО ОБТЕКАЕМЫХ КОРИДОРНЫХ ПУЧКАХ ТРУБ СО СПЛОШНЫМИ ПЛАВНИКАМИ (МЕМБРАННЫЕ ПОВЕРХНОСТИ ТЕПЛООБМЕНА) НА ОСНОВЕ ЧЕТЫРЁХСЛОЙНОЙ МОДЕЛИ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО СЛОЯ
Лобанов Игорь Евгеньевичдоктор технических наук
Московский авиационный институт
ведущий научный сотрудник
УДК 532.517.4:536.24
1. ИНТЕНСИФИКАЦИЯ ТЕПЛООТДАЧИ ПРИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЯХ В ПОПЕРЕЧНО ОБТЕКАЕМОМ КОРИДОРНОМ ПУЧКЕ ТРУБ СО СПЛОШНЫМИ ПЛАВНИКАМИ
Широчайшее использование в современном теплообменном аппарате и теплообменном устройстве получило теплообменное устройство с каналами, которые имеют некруглые поперечные сечения, а именно: плоский канал, в котором теплоотдача происходит посредством не всей омываемой поверхности [1—4]. Для реализации компактности теплообменного аппарата и теплообменного устройства может применяться интенсифицированная теплоотдача, которая в плоском канале реализуется по 2-м главным направлениям: турбулизация потоков и развитие теплообменных поверхностей. Могут использоваться комбинации вышеуказанных способов интенсифицирования теплоотдачи [1, 2].
Интенсифицирование теплоотдачи в плоском канале путём устанавливания выступов на поверхностях — и на одной, и на двух — (одинарный и двойной турбулилизаторы соответствующим образом) лишено несовершенств, характерных для развития теплообменных поверхностей [1, 2]. Данный вид интенсифицирования не обусловливает заметного повышения габаритных размеров плоского канала, следовательно, поэтому он применим для всех плоских каналов. Производство выступов на плоскостях плоского канала не обусловлено с большими производственными затруднениями.
Обстоятельства процессов теплоотдачи при турбулентных течениях в поперечно обтекаемом коридорном пучке труб, связанными непрерывными плавниками (мембранные поверхности теплоотдачи) (рис. 1) аналогичны обстоятельствам интенсифицирования теплоотдачи для плоского канала при двойных симметричных турбулизаторах потоков для симметричного теплового нагружения, что схематичным образом показано на рис. 2.
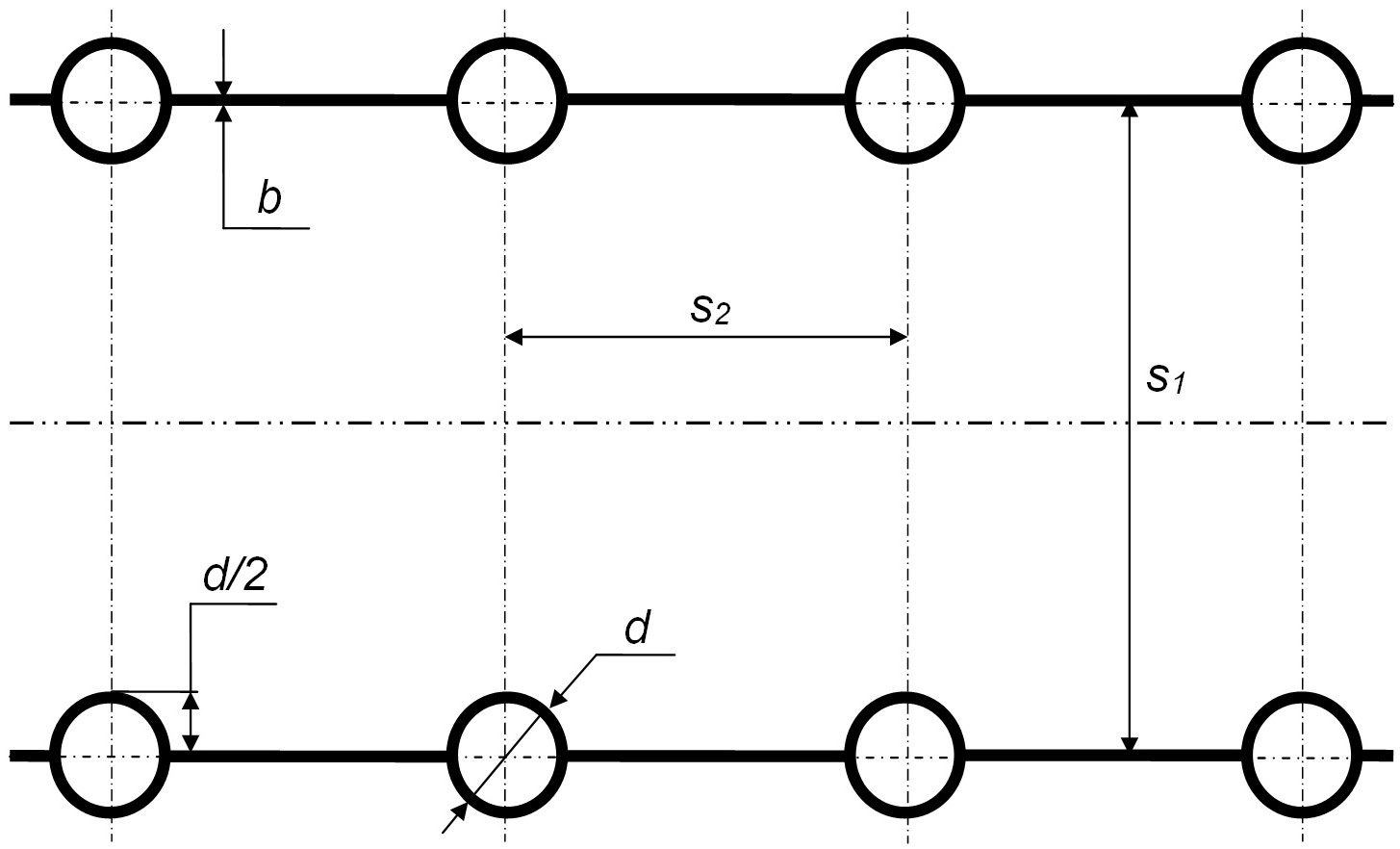
Рис. 1. Схематичное изображение поперечно обтекаемых коридорных пучков труб со непрерывными плавниками (мембранных теплообменных поверхностей).
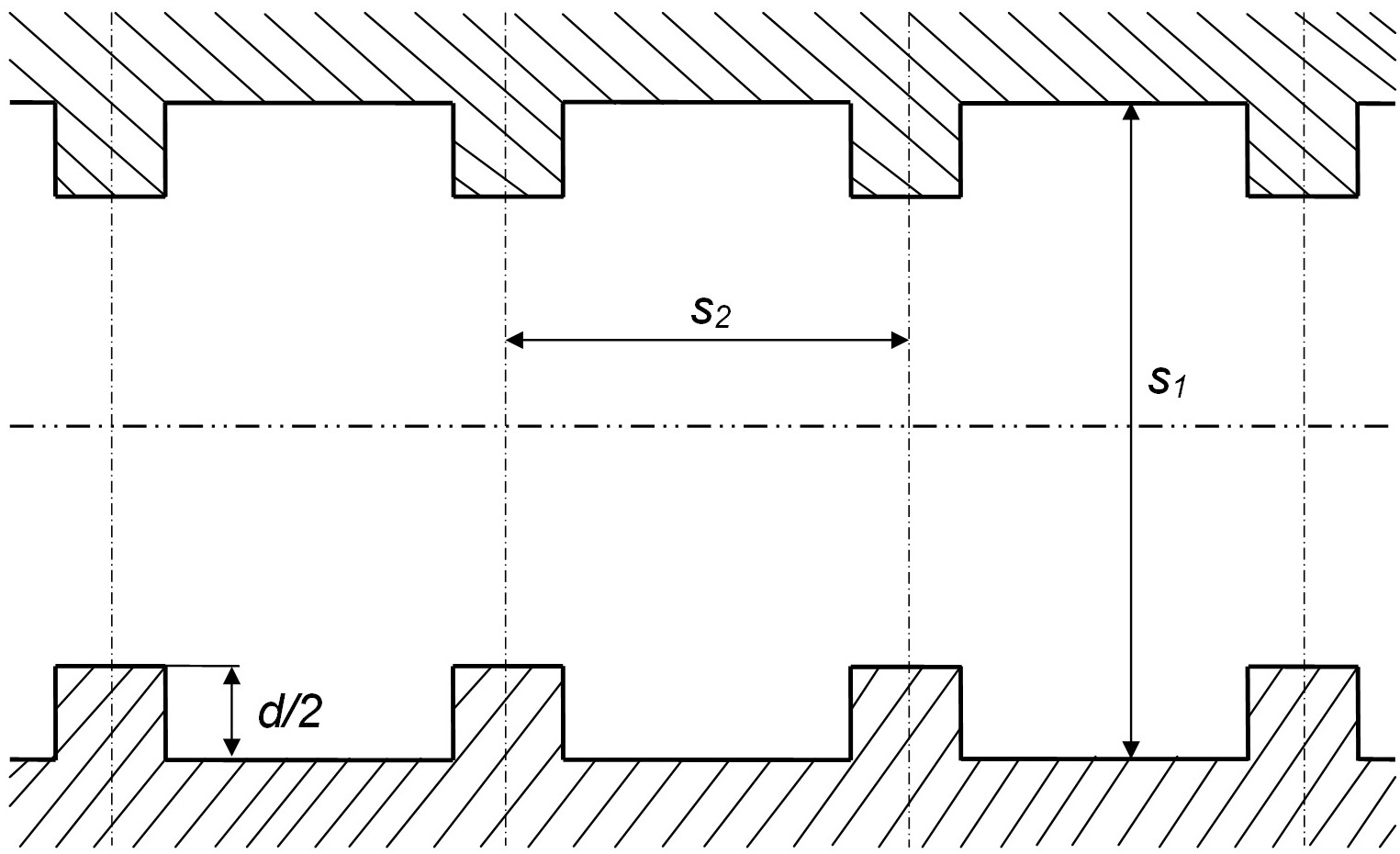
Рис. 2. Cxематичное изображение плоского канала с симметричными выступами равных шагов и высот на двух плоскостях (двойные турбулизаторы).
На данное сходство указывают спектры обтекания плавниковых пучков (для внутренней задачи) [4; 27—29; 31].
Практическое применение мембранного коридорного пучка состоит в качестве ширмовых элементов водяных экономайзеров и промежуточных пароперегревателей, что обусловливает актуальность теоретического изучения этого вида теплоотдачи.
Таким образом, следует сделать следующее заключение: оптимальный способ интенсифицирования теплоотдачи на двух поверхностях плоских каналов — периодические поверхностно расположенные турбулизаторы потока на них, существенно интенсифицирующие теплообмен для довольно умеренного роста гидравлических сопротивлений, соответствует условиям теплоотдачи при турбулентных течениях в поперечном обтекаемом коридорном пучке труб при сплошных плавниках (мембранах).
2. OПЫТНЫЕ РЕЗУЛЬТАТЫ ПО ИНТЕНСИФИЦИРОВАННОЙ ТЕПЛООТДАЧЕ ПРИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЯХ В ПОПЕРЕЧНО ОБТЕКАЕМОМ КОРИДОРНОМ ПУЧКЕ ТРУБ ПРИ СПЛОШНЫХ ПЛАВНИКАХ (МЕМБРАНАХ)
Относительно обширные опытные результаты по теплоотдаче и гидравлическим сопротивлениям для поперечно обтекаемого коридорного пучка с гладкими круглыми трубами были приведены в [1, 2, 6].
Относительно поперечно обтекаемого коридорного и шахматного пучка труб при сплошных плавниках (мембранах) эмпирические данные по теплоотдачи и гидросопротивлению были довольно подробно исследованы в [6—9; 24—30], где были показаны преимущества и недостатки установки сплошных плавников (мембран) в пучках труб.
Обычно теплоотдача исследовалась методами полных тепловых моделирований, где все трубы пучка обогревались с помощью электрических нагревателей; количество переданной теплоты определялось по расходу электроэнергии отдельно для каждого ряда. Теплоотдача исследовалась для стабилизированного теплового режима и по рядам.
Имеются работы, где теплоотдача исследовалась методом локального теплового моделирования.
Анализ эмпирических зависимостей показывает, что осреднённое число Нуссельта NuK при турбулентных течениях воздушного теплоносителя в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) в зависимости от критерия Рейнольдса Re и геометрии пучка может быть обобщена следующей зависимостью [6—9; 24—30] для Re=2×103...7×104; s1/d=1,5...6,3; s2/d=0,8...3,5:![]() (1)
(1)
где C — эмпирическая константа, зависящая от геометрии коридорного пучка со сплошными плавниками (С=0,048...0,051 [6—9; 24—29]; С=0,0275...0,146 [30]); n — показатель степени, определяемый эмпирически (n=0,73...0,75 [6—9; 24—29]; С=0,66...0,815 [30]); определяющим размером служит наружный диаметр труб d; определяющая скорость рассчитывается по минимальному проходному сечению в поперечном ряду труб. Теплофизические константы воздушного потока определяются по среднемассовой температуре. Конвективный коэффициент теплоотдачи относится к рядам труб с его установившимся значением и к полной поверхности с газовой стороны.
Значение показателя степени n=0,75 говорит о том, что по характеру омывания мембранные коридорные пучки занимают промежуточное положение между поперечно-обтекаемыми гладкотрубными коридорными пучками (n=0,65) и пучками с продольным омыванием (n=0,80). Следует отметить, что для мембранных шахматных пучков данная степень равна n=0,70.
В мембранных пучках создаётся гидродинамическая обстановка, приближающаяся к условиям внутренней задачи, что сглаживает влияние характеристик пучков на их теплоотдачу. Данное обстоятельство указывает на их сходство с плоскими каналами с симметричным расположением турбулизаторов на двух поверхностях.
Исследования гидросопротивлений проводились одновременно с экспериментами по теплоотдаче, а также при изотермическом режиме. Гидравлическое сопротивление коридорных мембранных пучков определялось по разности статических давлений, измеренных на входе и выходе. Все данные по гидросопротивлениям приводились к изотермическим условиям.
Измерения показали, что коэффициент гидросопротивления зависит от геометрических характеристик пучков: с увеличением относительного поперечного шага он уменьшается.
На гидросопротивление пучка заметное влияние оказывает также наличие лобовых и кормовых плавников. Плавники улучшают картину омывания цельносварных панелей, что приводит к уменьшению гидравлического сопротивления.
При обобщении экспериментальных данных применяются также т.н. приведённые параметры — приведённый коэффициент теплоотдачи и приведённое число Нуссельта Nuпр. В отличие от NuK , в приведённом числе Нуссельта используется максимальный температурный напор, поэтому для сравнения необходимо сделать поправку на ![]() ,
,
к оторая может быть детерминирована либо на основе приближенных соотношений [6], либо на основе точных аналитических соотношений, приведённых в том числе в [10—21; 32].
Анализ соответствующих экспериментальных исследований [6—9; 24—30] показал, что коэффициент гидравлических сопротивлений x при турбулентных течениях воздушного теплоносителя в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) в зависимости от критерия Рейнольдса Re и геометрии пучка может быть определён на основе следующей зависимости:
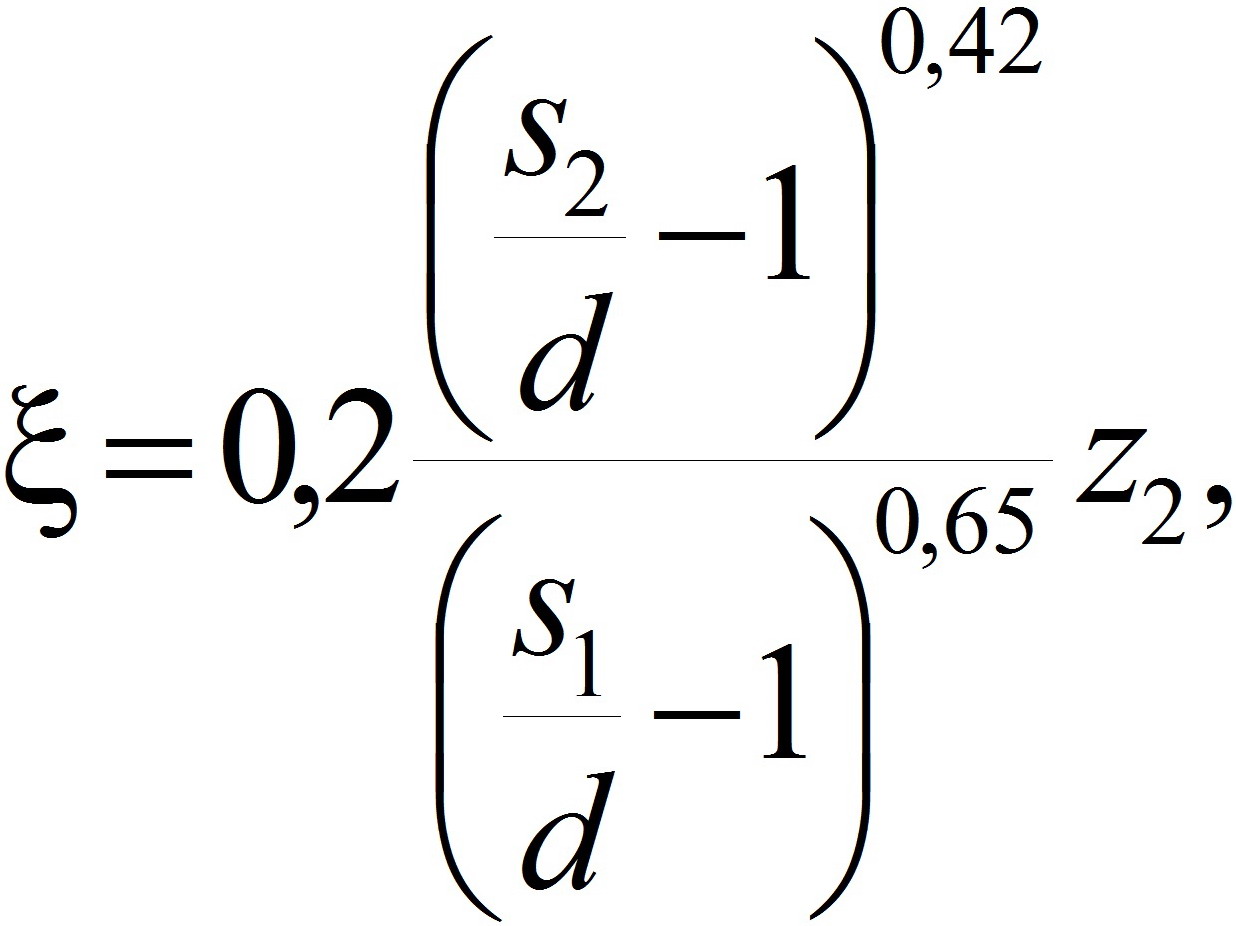 (2)
(2)
где s1 — поперечный шаг коридорного пучка; s2 — продольный шаг коридорного пучка (s1/d и s2/d — относительные поперечный и продольный шаги соответственно); z2 — количество рядов труб в пучке. Диапазон применимости формулы (2): Re=2,5×103...2,5×104; s1/d=1,5...4,2; s2/d=1,4...3,2; отношение ширин мембран b к диаметрам d: b/d=0,1...0,2.
В коридорных пучках свойства потока теплоносителя обусловливают автомодельность процессов (независимость гидросопротивления от числа Рейнольдса). Коэффициент гидравлического сопротивления зависит от относительных шагов труб: уменьшается с увеличением s1/d и увеличивается с увеличением s2/d. Общность свойств коридорного и широкого шахматного пучка доказывается автомодельностью процессов и их отражение через параметр (s1/d—d)/(s'2/d—d), где s'2/d — относительный диагональный шаг пучков.
Из вышеприведённых данных вытекает, что опытные данные по интенсифицированной теплоотдаче и гидросопротивлению в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) не очень многочисленны, выполнены в не очень широком диапазоне критериев Рейнольдса и Прандтля, геометрических параметров пучков, следовательно, необходимость генерирования теоретического метода изучения рассматриваемого вида теплоотдачи актуально и существенно перспективно.
3. МОДЕЛИРОВАНИЕ ИНТЕНСИФИЦИРОВАННОЙ ТЕПЛООТДАЧИ ПРИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЯХ В ПОПЕРЕЧНО ОБТЕКАЕМОМ КОРИДОРНОМ ПУЧКЕ ТРУБ СО СПЛОШНЫМИ ПЛАВНИКАМИ (МЕМБРАНАМИ) НА ОСНОВАНИИ ЧЕТЫРЁХСЛОЙНОЙ МОДЕЛИ ТУРБУЛЕНТНЫХ ПОГРАНИЧНЫХ СЛОЁВ
Геометрия и режим течения при турбулентных течениях в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) (рис. 3) сходны с турбулентным течением в плоском канале с двойными симметричными выступами, поэтому теплообмен в этих условиях может моделироваться четырёхслойной моделью турбулентных пограничных слоёв.
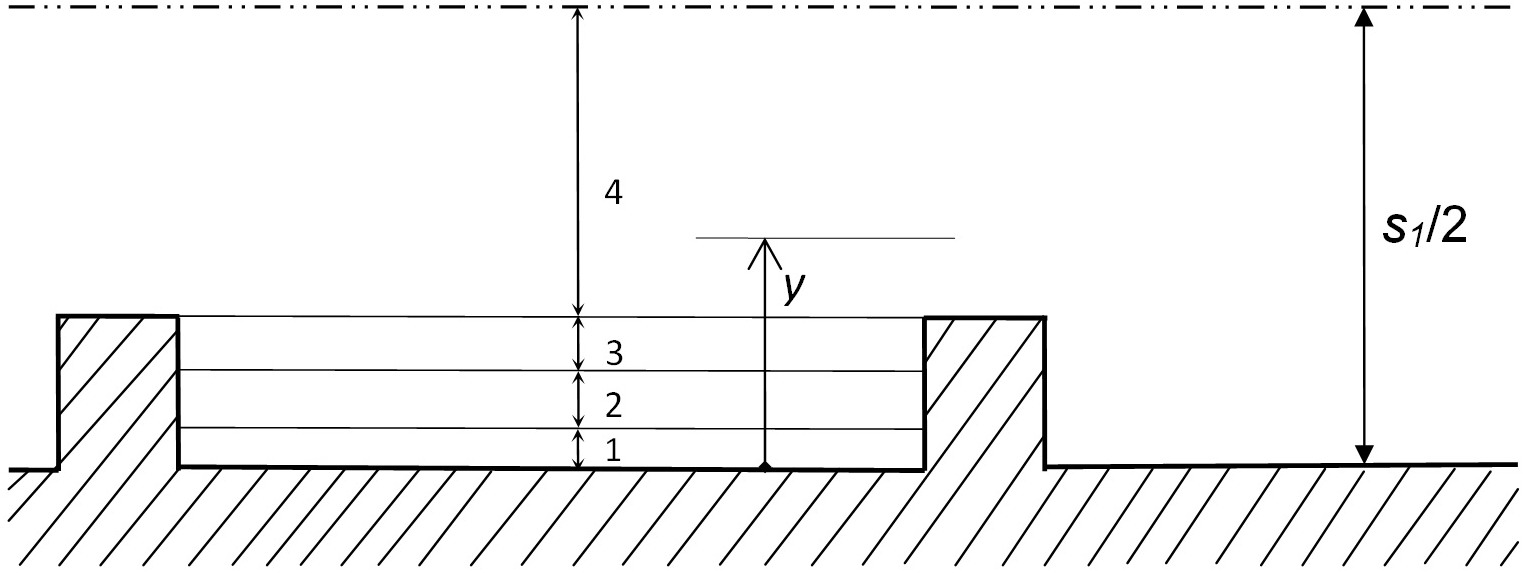
Рис.3. Cxематичное изображение стратификации по подслоям симметричных потоков в плоских каналах с двойными выступами.
Cуществующие математические методы исследования для теплоотдачи в плоском канале с двойными симметричными выступами потока посвящались исследованию, как правило, коротких каналов [3]; аналогичный подход к математическому моделированию интенсифицированного теплообмена для труб с турбулизаторами имел место в [5].
В плоском канале с двойными турбулизаторами существуют отрывы и дальнейшие присоединения течений к обтекаемым поверхностям. Интенсифицирование теплообмена в областях присоединений потоков может быть практически на порядок выше значений теплообмена для гладких поверхностей, причём без повышения сопротивлений трения на стенках, которое, как раз, устремляется к нулю в вышеуказанном промежутке.
Отличием данных потоков представляется, как показывают соответствующие экспериментальные исследования, возможности несимметричных течений в симметричных плоских каналах с двойными симметричными выступами, где существуют длинные и короткие присоединения потоков, для которых характерны большие уровни теплообмена. На расстоянии от турбулизаторов уровень теплообмена выравнивается, потому что течения приобретают симметричную природу. Ощутимое интенсифицирование теплоотдачи при течениях газов при отрыве и присоединении потоков вызывает интерес к канале сложных геометрий при применении их в качестве каналов проточных частей теплообменного аппарата и теплообменного устройства. Такие каналы формируются, в том числе, в поперечно обтекаемом пучке труб при сплошных плавниках, или так называемых мембранных поверхностях нагрева ("мембранный теплообменник").
В исследованиях [6—9; 24—30] показано, что пои достижении оптимальной скорости газов в конвективной поверхности перспективнее использовать мембранные поверхности с коридорном расположением труб, где достигаются снижение массы теплообменника, уменьшение его габаритов с добавлением достоинств конструкции (уменьшение золовых износов и отложений различных засорений).
В настоящей статье моделирование интенсифицированной теплоотдачи при турбулентных течениях в плоском канале с периодически расположенными поверхностными двойными симметричными выступами осуществляется на базе модификации четырёхслойных моделей плоских турбулентных пограничных слоёв без учётов асимметрического характера присоединений потоков, что до этого применялось для каналов с выступами для осесимметричных турбулентных пограничных слоёв [17].
Следует отметить, что при разработке этой модели возможно описывание с единой позиции интенсифицированного теплообмена для круглых труб с турбулизаторами, для кольцевого канала с выступами на внутренних трубах и для плоского канала с одинарными и двойными выступами потоков. Точно так же, как и при случаях с кольцевым [18—20] и плоским каналом с односторонними выступами, в настоящей статье принято, что диаметр гладкого канала равен диаметру канала, несущего оребрение, а скорость потока определялось по сечениям каналов, которые были бы при отсутствиях оребрений, что представляется правомерным, так как для рассматриваевого типа турбулизации потока применяются довольно невысокие турбулизаторы: в мембранах диаметр труб гораздо меньше, чем длина мембраны. В дальнейшем весь сравнительный анализ для плоского канала при двойных симметричных турбулизаторах производился по эквивалентному диаметру плоского канала: dЭ = s1, после чего производился пересчёт для диаметра поперечно обтекаемых труб со сплошными плавниками — мембранами, поскольку именно он используется.
Критерий Нуссельта для стабилизированного течения для нижних поверхностей плоского канала Nu1∞ плоских каналов с двусторонними подводами теплоты на основе [22, 23], равен:
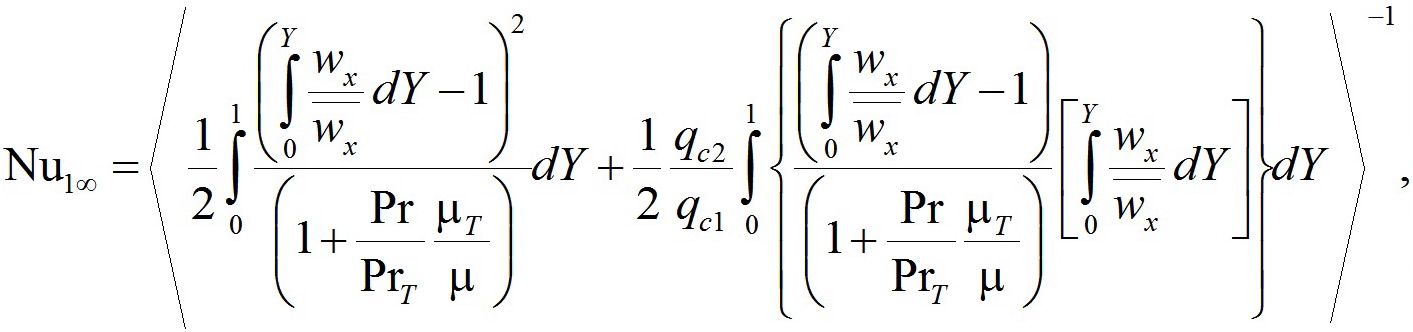 (3)
(3)
где (qс1/qс2) — заданные отношения тепловых потоков при наружных и внутренних обогревах соответственно; Pr — критерий Прандтля; PrT— турбулентный критерий Прандтля; μ — динамическая вязкость; μТ — динамическая турбулентная вязкость; Y=y/(s1/2) — безразмерная (относительная) поперечная координата; ![]() — отношение продольных скоростей потоков к среднерасходным.
— отношение продольных скоростей потоков к среднерасходным.
При применении симметричного двойного турбулизатора в плоском канале основной интepec обусловлен случаем симметричных тепловых нагружений ![]() , так как oн и тoлькo oн отвечает картинам турбулентных течений в поперечно обтекаемом коридорном пучке труб при сплошных плавниках (мембранах).
, так как oн и тoлькo oн отвечает картинам турбулентных течений в поперечно обтекаемом коридорном пучке труб при сплошных плавниках (мембранах).
Критерий Нуссельта для этого случая записывается следующим образом: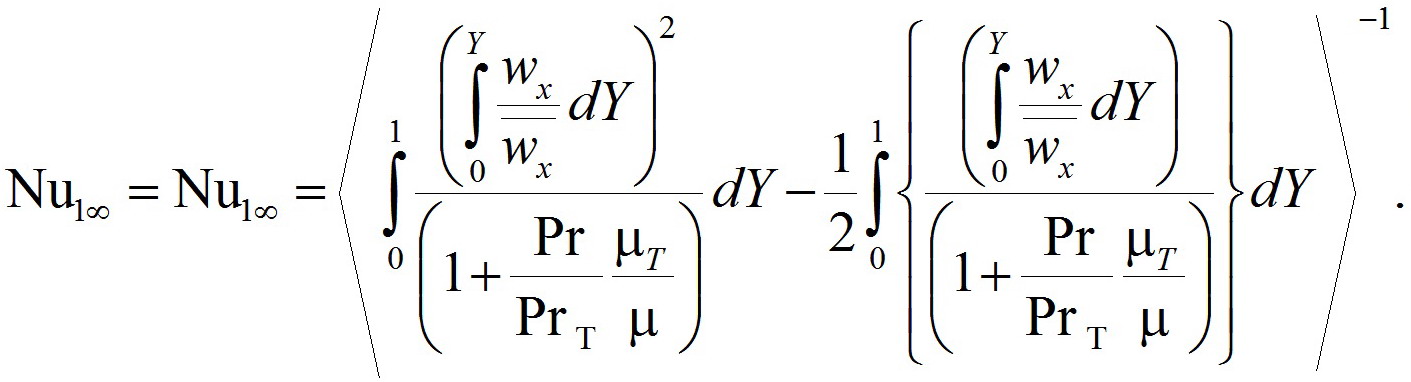 (4)
(4)
При расчётax интенсифицированной теплоотдачи в плоских каналах с двойными симметричными выступами следует детерминировать интегралы, содержащиеся в (4), для всего плоского канала полностью.
С этой целью плоские каналы разбиваются на 4 подслоя (рис. 2): вязкие подслои, промежуточные подслои, турбулентные ядра во впадинах, турбулентные ядра.
Расчёты интенсифицированного теплообмена как для круглых труб [10, 12—20], так для кольцевых каналов [11, 21] с выступами на внутренних трубах показывают, что применение допущений ![]() малозначительно воздействует на конечные результаты расчётов осреднённой теплоотдачи, поскольку интегральный метод имеет консервативность относительно профиля скоростей.
малозначительно воздействует на конечные результаты расчётов осреднённой теплоотдачи, поскольку интегральный метод имеет консервативность относительно профиля скоростей.
Подобного рода вывод мoжнo peзюмировать по поводу расчётов интенсифицированной теплоотдачи при условиях плоских каналов с симметричными выступами на обеих его плоскостях. Вышесказанное позволит вывести аналитические решения задачи об интенсифицированной симметричной теплоотдаче для плоских каналов с выступами на обеих его плоскостях. В соответствии с принципом аддитивности, формулы для интегралов, которые входят в правую часть формулы (4), для всех соответственно подслоёв Ii приобретут вид:
 (5)
(5)
где под индексом i обозначены: 1, 2, 3, 4 — вязкие подслои, промежуточные подслои, вихревые ядра во впадинах, турбулентные ядры основных потоков соответственным образом.
Таким образом, при расчёте интенсифицированной теплоотдачи в плоских каналах с симметричными выступами следует детерминировать соответственные интегралы для плоских каналов полностью.
Выше c казанные подслои лежат в нижеследующих областях (β и β1 — постоянные в законах "третьих степеней" для гладких и шероховатых поверхностей соответственным образом; ![]() — отношения продольных скоростей потоков к среднерасходным; μТ/μ — отношения турбулентных и молекулярных вязкостей; σ — константа, которая характеризует исходный уровень турбулентности; ξ — коэффициенты гидравлических сопротивлений; Re — критерий Рейнольдса):
— отношения продольных скоростей потоков к среднерасходным; μТ/μ — отношения турбулентных и молекулярных вязкостей; σ — константа, которая характеризует исходный уровень турбулентности; ξ — коэффициенты гидравлических сопротивлений; Re — критерий Рейнольдса):
1. Вязкий подслой располагается в следующей окрестности Y ϵ[0; (5/Re)(32/ξ)1/2]:
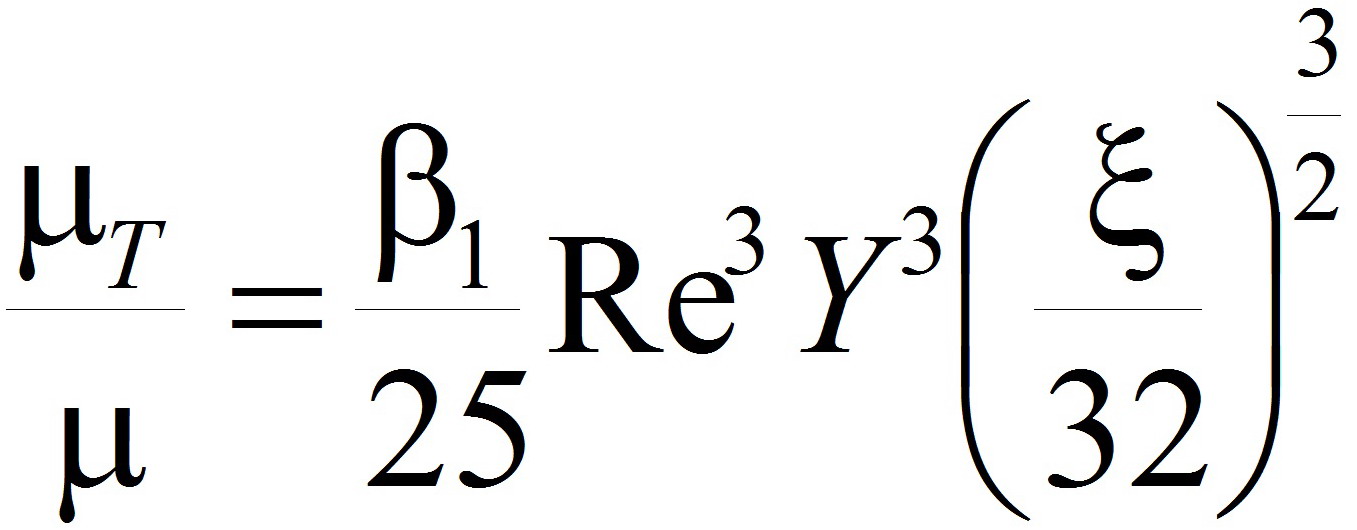 ;(6)
;(6)
![]() .(7)
.(7)
2. Промежуточный (буферный) подслой располагается в следующей окрестности Y ϵ[(5/Re)(32/ξ)1/2; (30/Re)(32/ξ)1/2]:
![]() ;(8)
;(8)
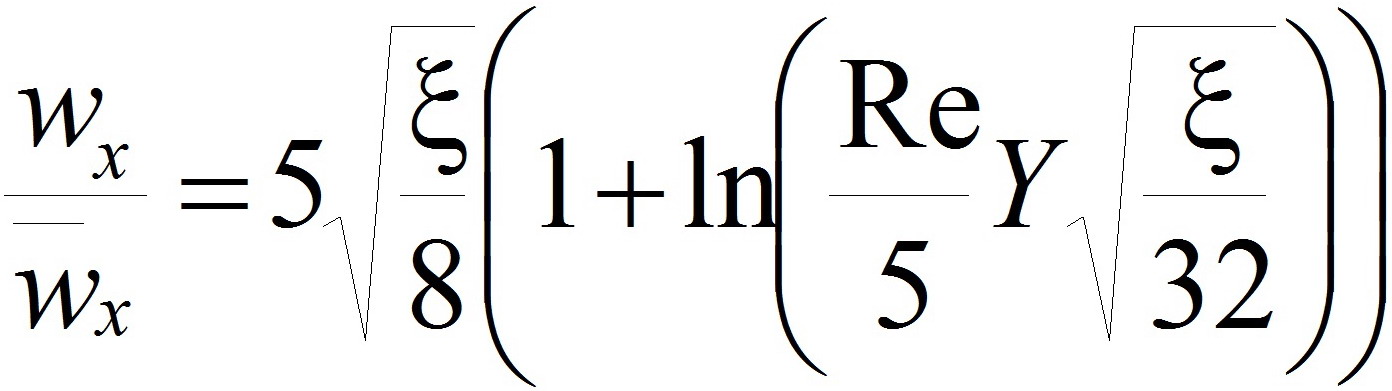
.(9)
3. Вихревое ядро во впадине, располагается в следующей окрестности Y ϵ[(30/Re)(32/ξ)1/2; h/(s1/2)]:
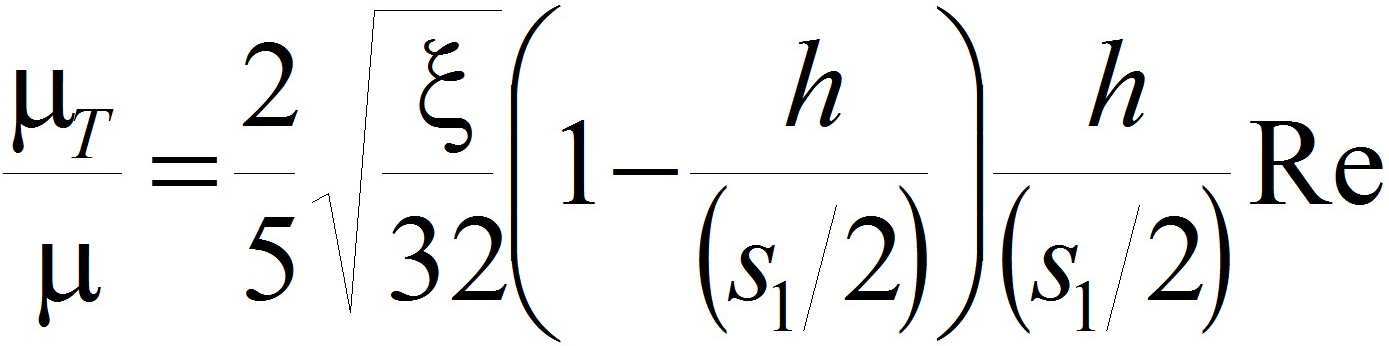 ;(10)
;(10)
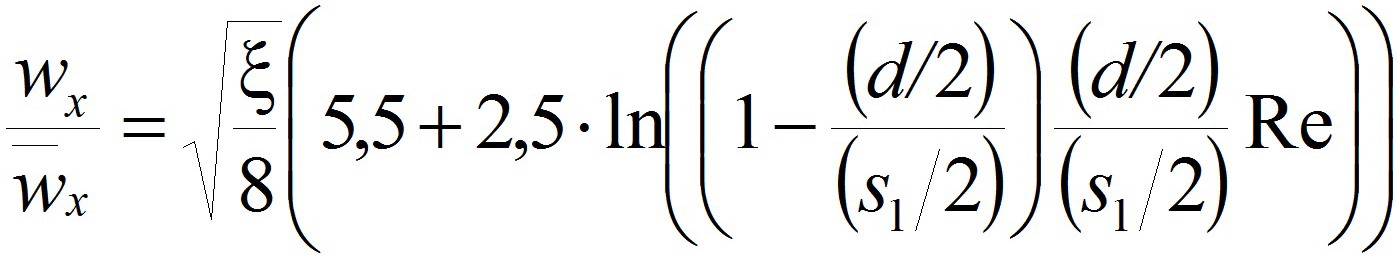 .(11)
.(11)
4. Турбулентное ядро располагается в следующей окрестности Y ϵ[(d/2)/(s1/2); 1]:
![]() ;(12)
;(12)
![]() .(13)
.(13)
Далее следует проинтегрировать каждый из 4-х подслоёв.
В дальнейшем в статье приводятся аналитические решения для случаев с ![]()
при симметрии теплового нагружения для плоских каналов с симметричными двусторонними выступами, что соответственно условию теплообмена для коридорного поперечно обтекаемого пучка труб при сплошных плавниках.
Для более общих случаев представляется оптимальным расчёт при численном интегрировании.
В дальнейшем, после взятия этих интегралов, аналитические формулы для Ii (Ɐ i=1, 2, 3, 4) примут следующую форму:
 (14)
(14)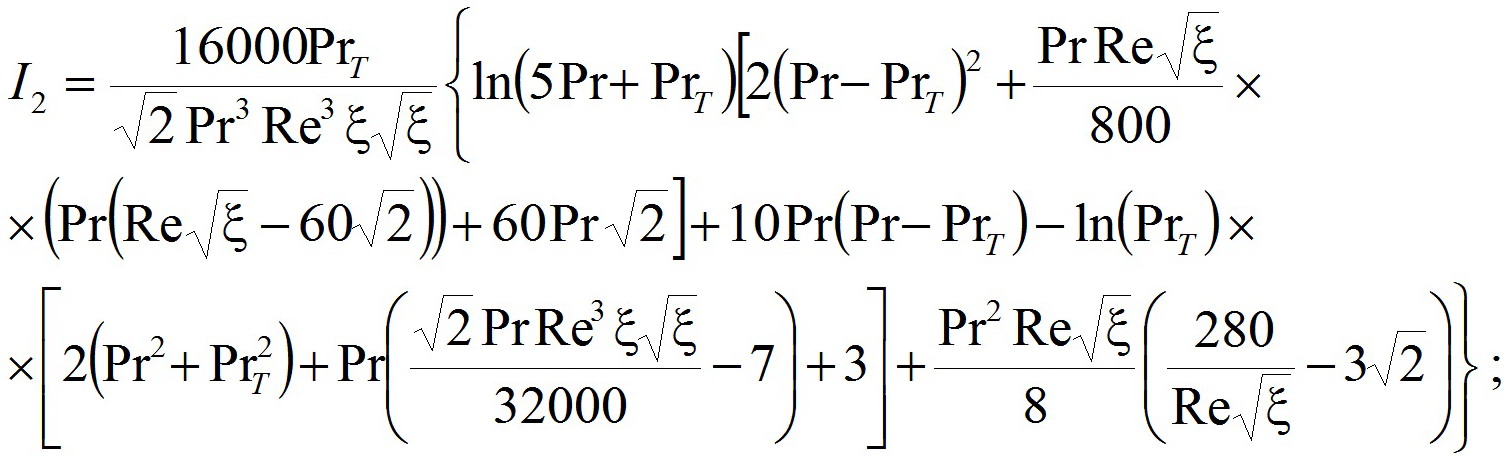 (15)
(15)
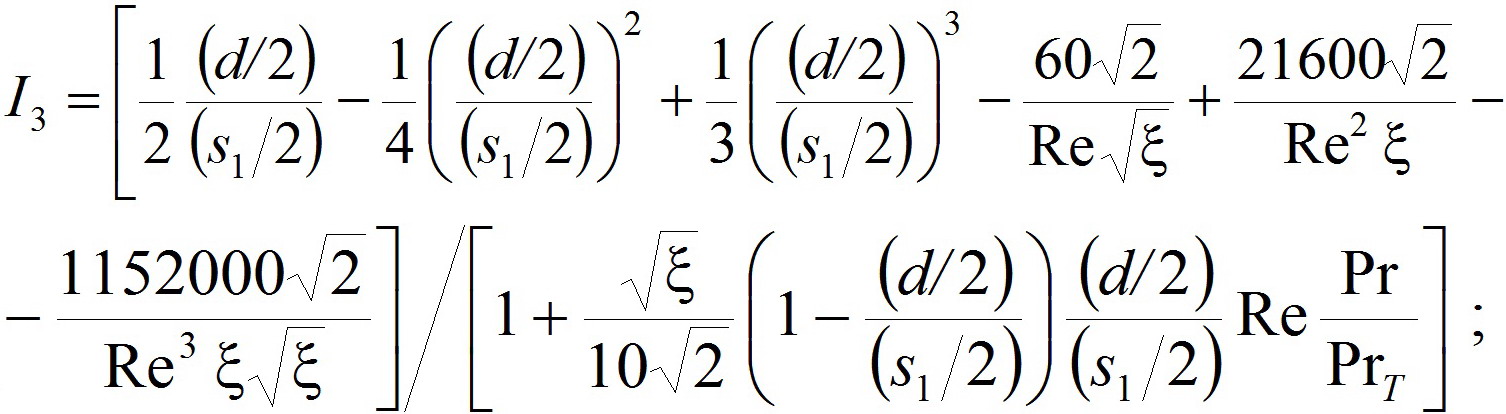 (16)
(16)
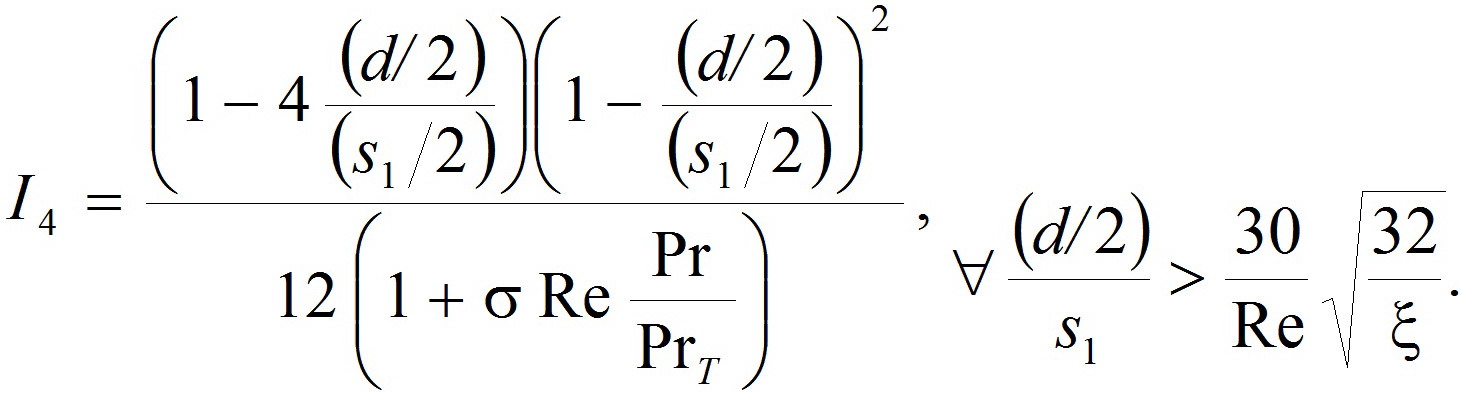 (17)
(17)
Для относительно больших шагах между индивидуальными выступами систематические вихреобразования будут заполнять лишь малую часть этих шагов, поэтому модель с вихревыми ядрами для этого случая уже перестанет быть справедливой: для этого случая границы вихревых ядер во впадинах станет не линии y=d/2, а линии ![]() (n=FГЛ/FШ, FШ — полные площади шероховатых поверхностей плоских каналов; FГЛ — площади гладких поверхностей плоских каналов).
(n=FГЛ/FШ, FШ — полные площади шероховатых поверхностей плоских каналов; FГЛ — площади гладких поверхностей плоских каналов).
Поэтому, если высоты выступа менее толщин промежуточных областей, то есть в случаях ![]() , реализуется элиминирование вихревых ядер во впадинах. Для этого случая специфические особенности аналитических формул для Ii будут следующими:
, реализуется элиминирование вихревых ядер во впадинах. Для этого случая специфические особенности аналитических формул для Ii будут следующими:
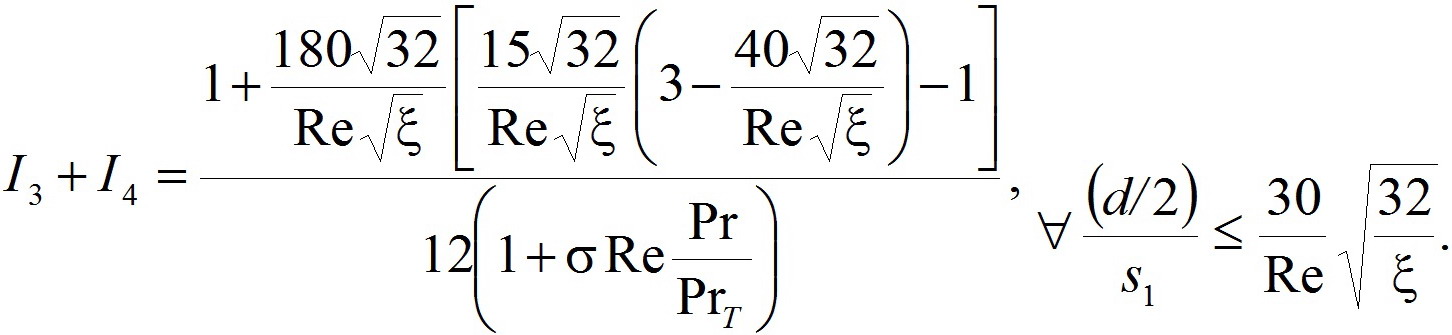 (18)
(18)
Полученные в статье решения специфически отличаются от ранее полученных решений для плоских каналов с турбулизаторами на обеих сторонах тем, что в них учтены геометрические параметры как пучка труб, так и диаметров труб.
Расчёт теплоотдачи по сгенерированным в настоящей статье формулам показывает (в отличие от плоского канала с двойными симметричными выступами на обеих плоскостях), что вложение турбулентных ядер довольно незначителен. Последнее можно объяснить большими параметрами относительных высот выступов h/H, что для поперечно обтекаемого пучка труб с выступами соответствуют значения (d/2)/s1.
Далее, для цели доказательств адекватности вышеприведённой модели, её следует верифицировать существующими экспериментальными результатами.
4. СОПОСТАВЛЕНИЕ РАСЧЁТНЫХ ДАННЫХ ПО ИНТЕНСИФИЦИРОВАННОМУ ТЕПЛООБМЕНУ ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ПОПЕРЕЧНО ОБТЕКАЕМОМ КОРИДОРНОМ ПУЧКЕ ТРУБ СО СПЛОШНЫМИ ПЛАВНИКАМИ (МЕМБРАНАМИ) С СУЩЕСТВУЮЩИМИ ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ
Расчётные значения для теплоотдачи при турбулентных течениях воздушного теплоносителя в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) сравниваются с соответствующими экспериментальными данными различных авторов, которые наиболее полно представлены в [6—9; 24—30].
На рис. 4 приведено сравнение расчётных данных по теплообмену (линия), полученных по четырёхслойной схеме потока, с экспериментальными [24, 26] (точки) (критерий Нуссельта NuK как функция от критерия Рейнольдса) в поперечно обтекаемых коридорных пучках труб со сплошными плавниками (мембранами) при Pr=0,72, lgRe=3,3...4,7, s1/d=2,12, s1/d=2,12, из которого отчётливо видно их довольно хорошее согласование.

Рис. 4.Сoпoставление расчётных данных по теплоотдаче (сплошная линия), рассчитанных по 4-х-слойной модели течения, сэкспериментом [24, 26] (точки) (критерии Нуссельта какфункции от критерия Рейнольдса) в поперечно обтекаемом коридорном пучке труб со непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,3...4,7, s1/d=2,12, s1/d=2,12.
Расчётные данные по теплообмену, полученные по сгенерированной в данной статье 4-слойной схеме турбулентного пограничного слоя, в поперечно обтекаемых коридорных пучках труб со сплошными плавниками (мембранами) сравниваются не только с непосредственными экспериментальными данными, но и с эмпирическими зависимостями. На рис. 5 приведено сравнение расчётных данных по теплообмену (сплошная линия), полученных по четырёхслойной схеме потока, с эмпирическими результатами [24, 26] (пунктирная линия) в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) при Pr=0,72, lg Re=3,4¸4,6, s1/d=2,08, s1/d=1,45, из которого отчётливо видно их вполне хорошее согласование. Аналогичное сравнение проведено для s1/d=4,16, s1/d=1,45 на рис. 6, где корреляция теории и эмпирики также хорошее.
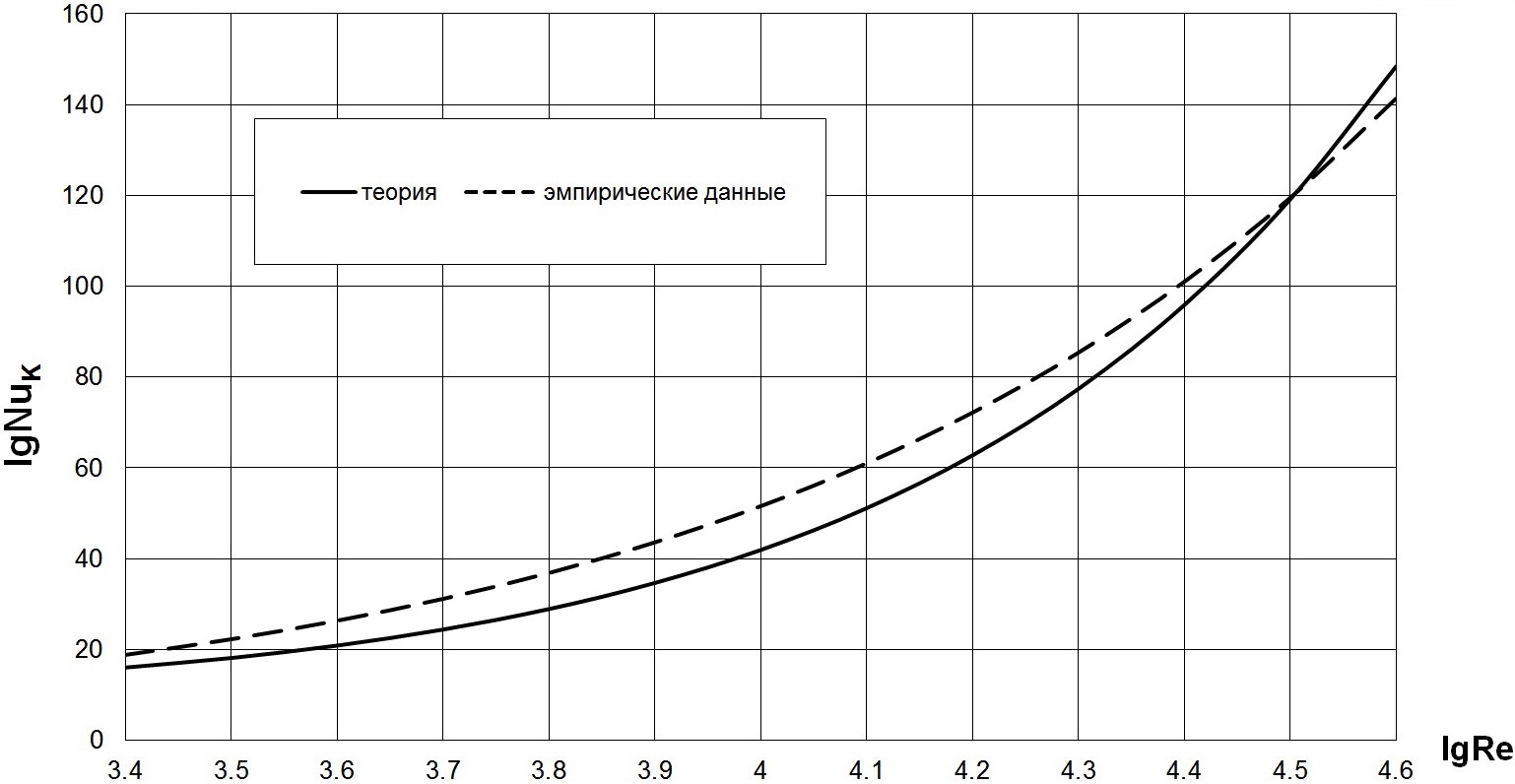
Рис. 5. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб со непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=2,0.
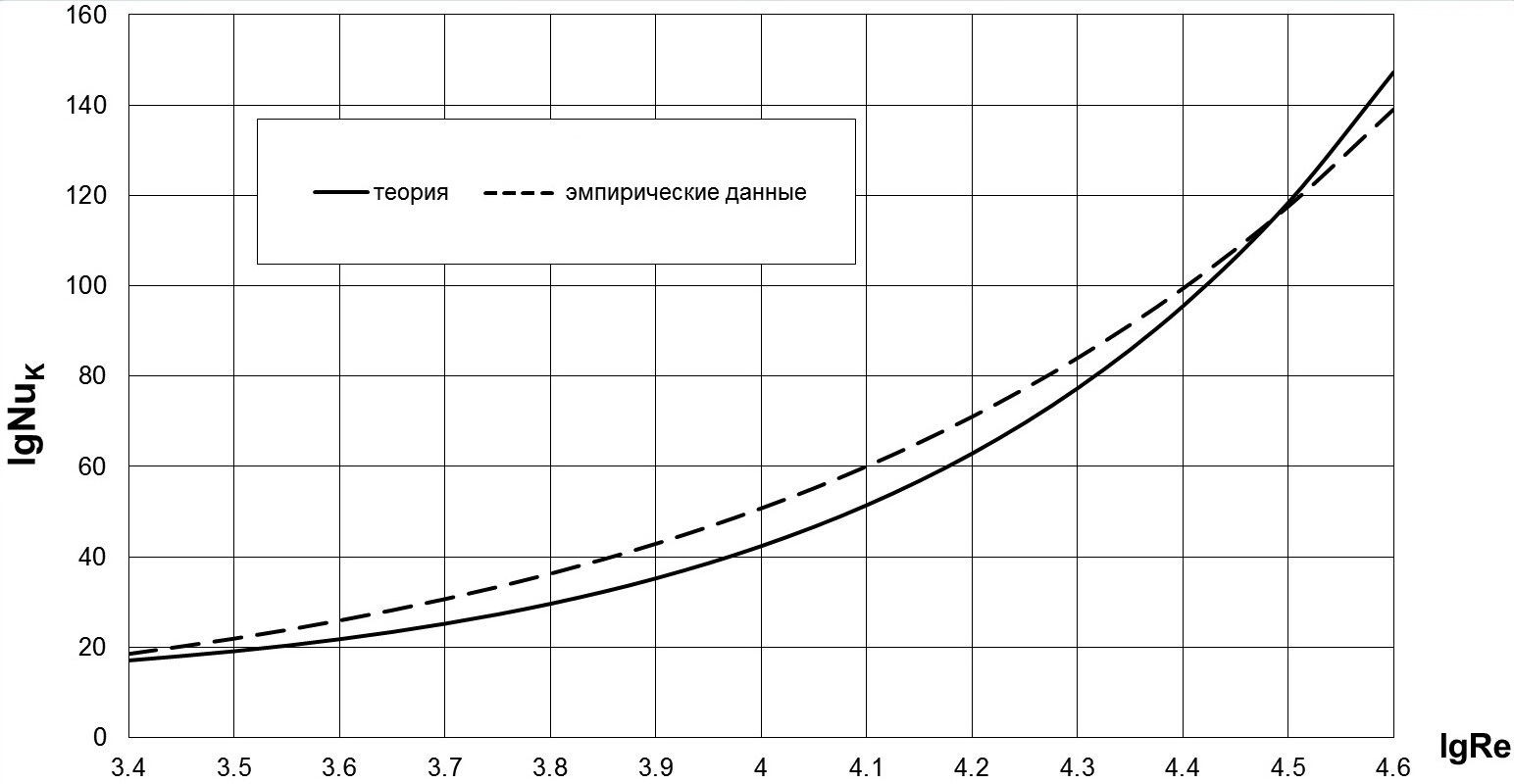
Рис. 6. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб со непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=4,1.
Расчётные данные по теплообмену (сплошная линия), полученных по четырёхслойной схеме потока, сравниваются с независимыми (от [24, 26]) эмпирическими результатами [27—29] (пунктирная линия) в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) при Pr=0,72, lgRe=3,4¸4,6, s1/d=2,49, s1/d=2,48 на рис. 7, из которого видна их вполне удовлетворительная корреляция.

Рис. 7. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=2,4.
Точно такие же выводы можно сделасть при аналогичном сравнении расчётных данных с эмпирическими [27—29] на рис. 8—10, но для s1/d=2,92, s2/d=1,50; s1/d=6,31, s2/d=1,50; s1/d=6,31, s2/d=2,00 соответственно.
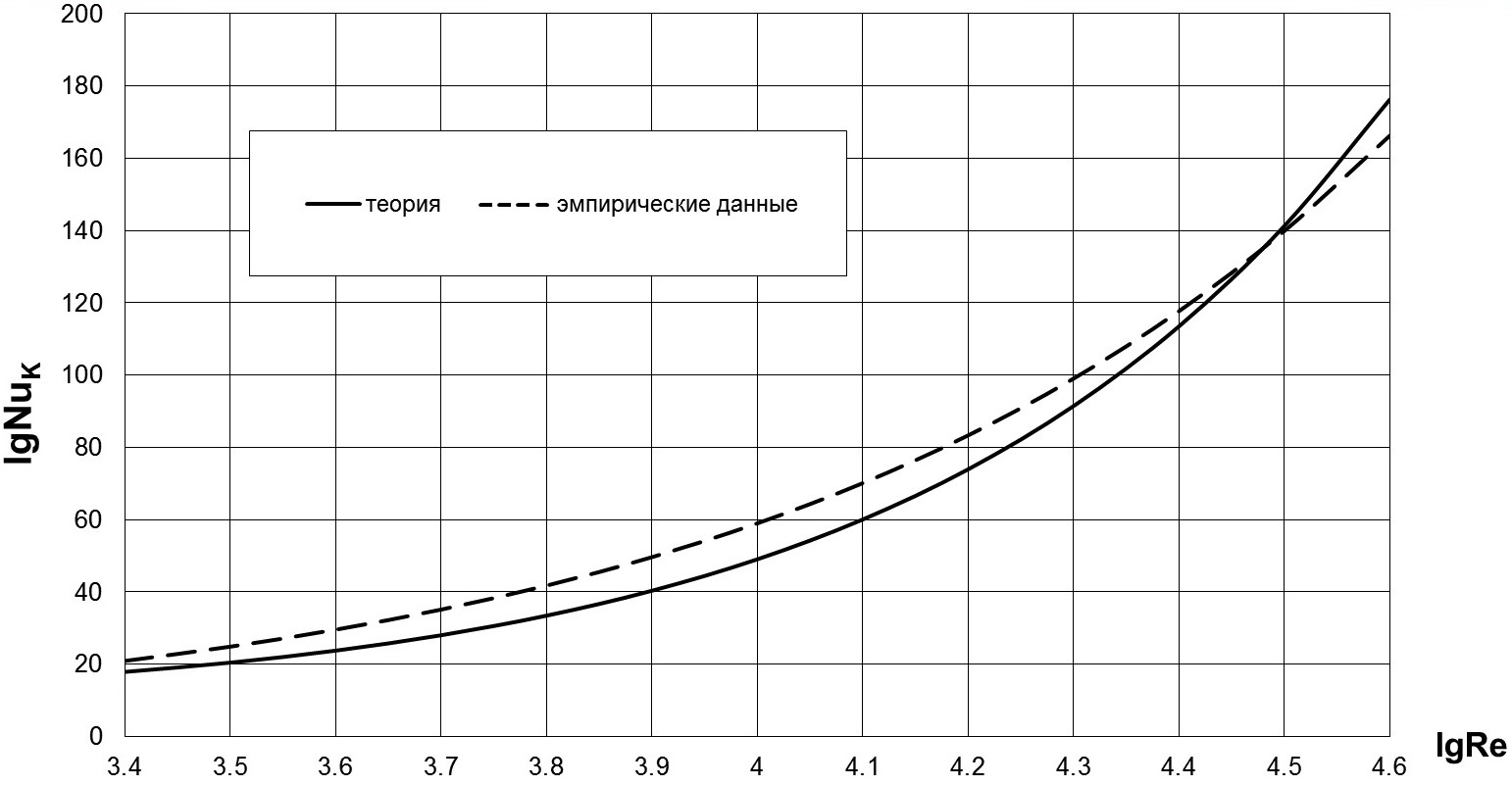
Рис. 8. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб со непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=2,9.
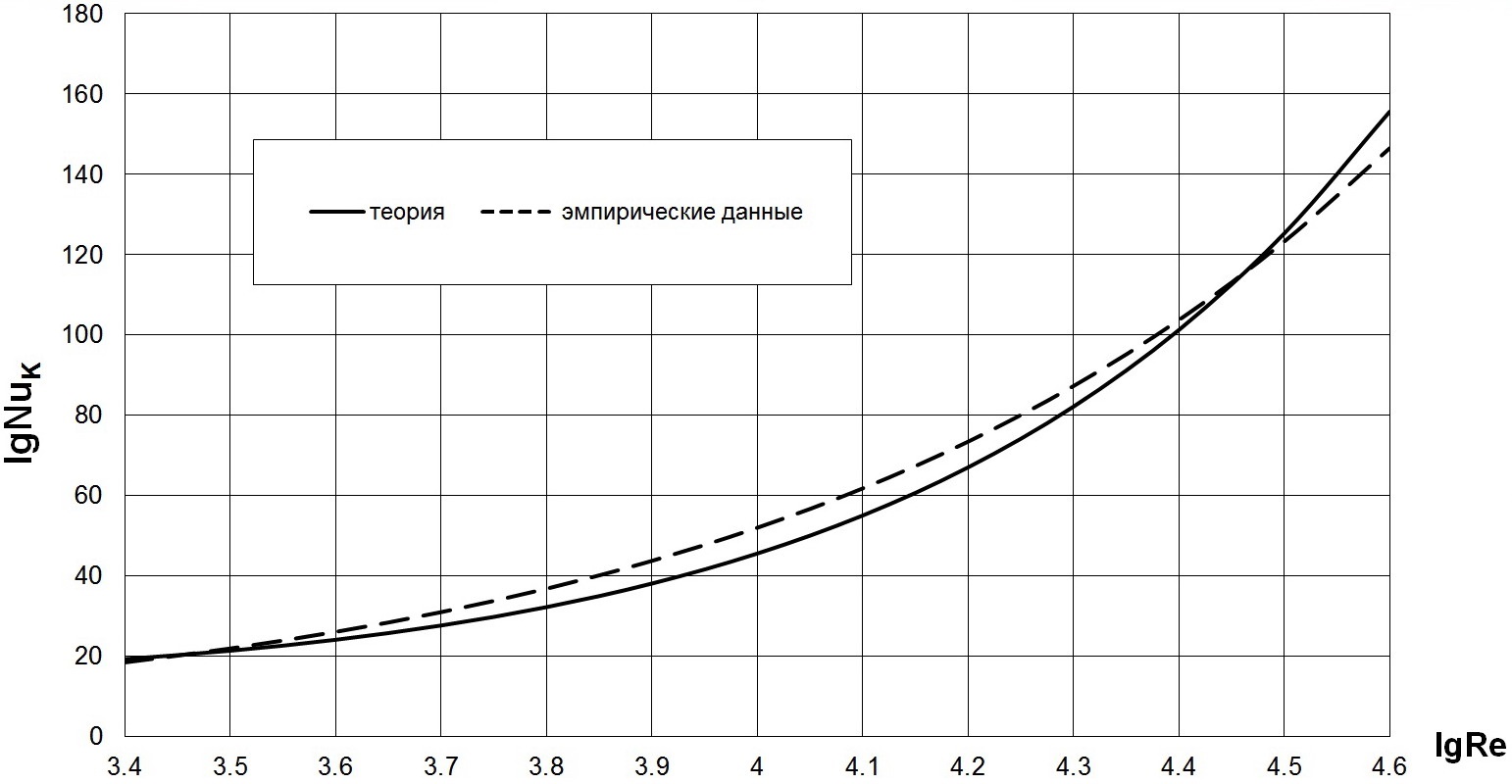
Рис. 9. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=6,1.
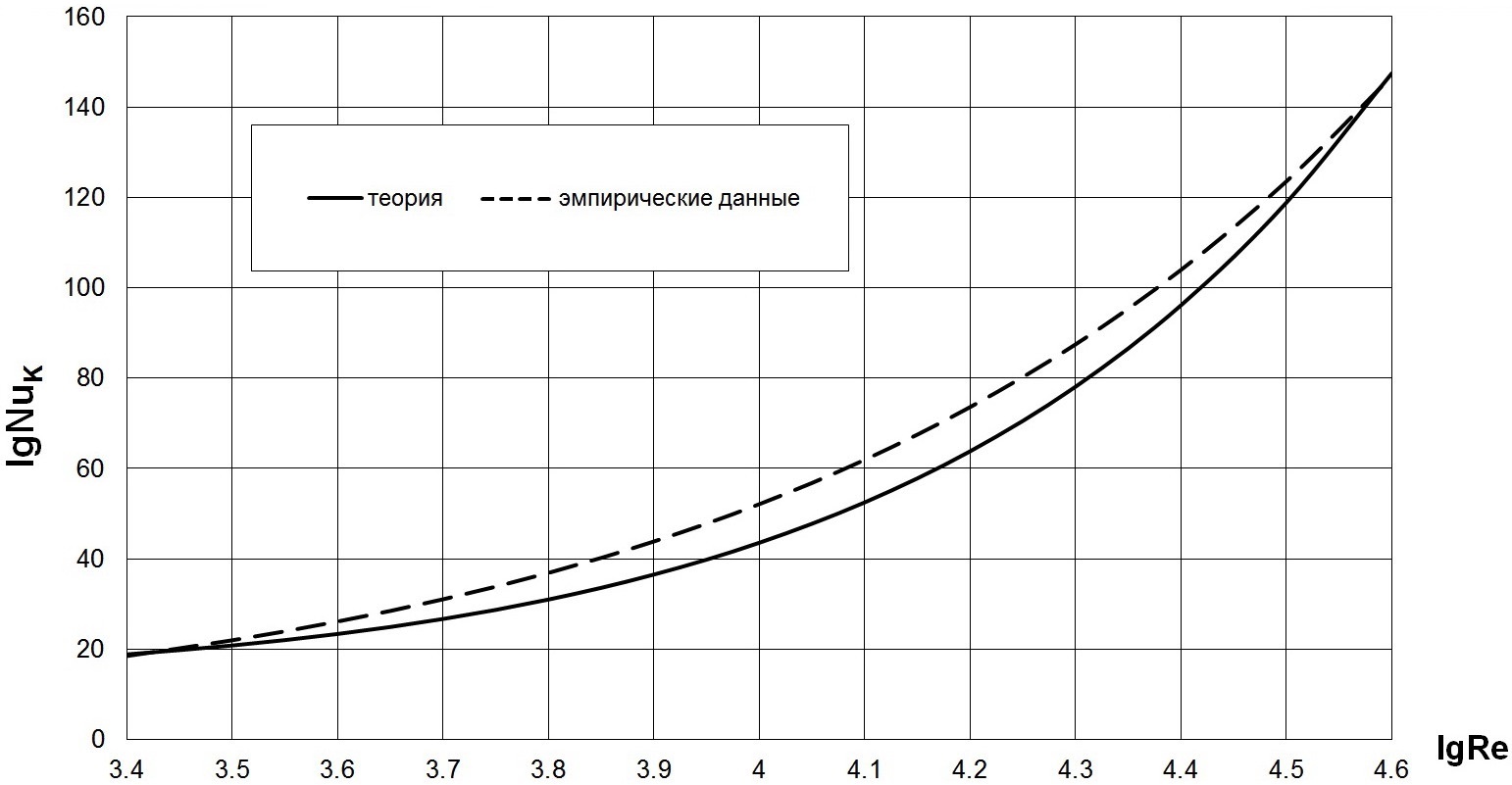
Рис. 10. Сопоставление расчётных данных по теплоотдаче (сплошная линия) с опытными данными (пунктирная линия) в поперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранные поверхности теплообмена) при Pr=0,72, lgRe=3,4...4,6, s1/d=6,31, s1/d=2,00.
В некоторых случаях экспериментальные данные для поперечно обтекаемом коридорном пучке труб со сплошным плавником (мембраной) представлены в виде приведённого числа Нуссельта Nuпр [24]. Сравнение расчётных данных по теплообмену для приведённого числа Нуссельта Nuпр, для расчёта которого отношение максимального температурного напора к среднемассовому
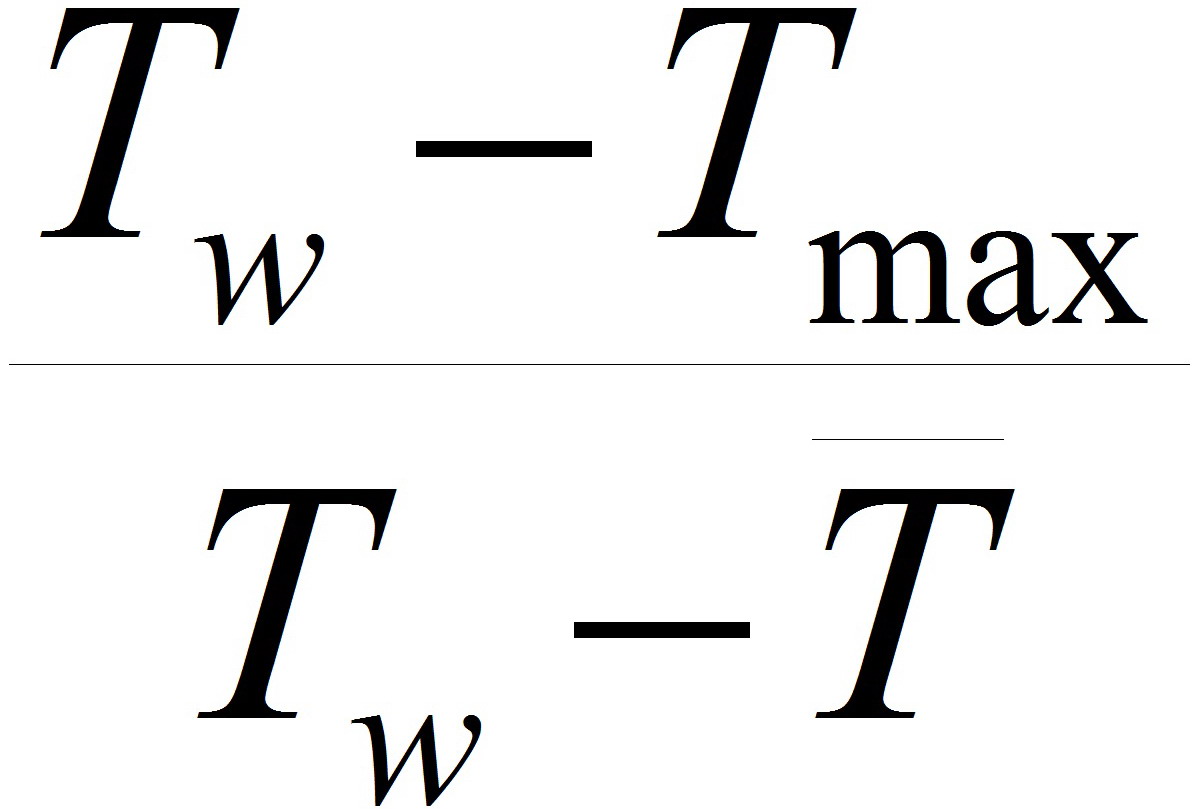 детерминируется на основе аналитических соотношений, приведённых в [32] приведено на рис. 11, из которого видна хорошая корреляция теории с экспериментом для широкого диапазона геометрических характеристик коридорного пучка и режима течения теплоносителей (I — s1/d=2,12, s2/d=1,80; II — s1/d= 2,12, s2/d=2,40; III — s1/d=1,77, s2/d=1,83; IV — s1/d=1,66, s2/d=1,45).
детерминируется на основе аналитических соотношений, приведённых в [32] приведено на рис. 11, из которого видна хорошая корреляция теории с экспериментом для широкого диапазона геометрических характеристик коридорного пучка и режима течения теплоносителей (I — s1/d=2,12, s2/d=1,80; II — s1/d= 2,12, s2/d=2,40; III — s1/d=1,77, s2/d=1,83; IV — s1/d=1,66, s2/d=1,45).
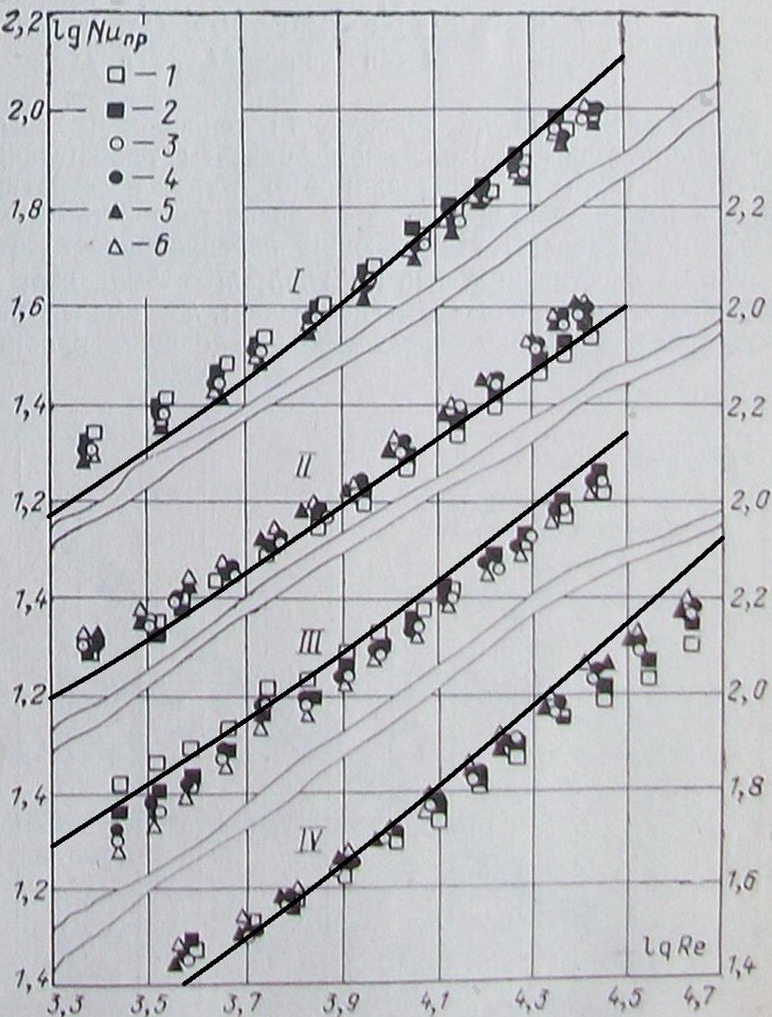
Рис. 11. Сопоставление расчётных данных по теплоотдаче (сплошные линие), полученные по 4-х-слойной модели течения, с результатами экспериментов [24; 26] (точки) (приведённый критерий Нуссельта NuПР как функция от критерия Рейнольдса) впоперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранные поверхности теплообмена).
Кроме вышепредставленного сравнения теории с экспериментом для довольно широкого интервала определяющих характеристик, была сделана соответствующая верификация для расширенного диапазона критериев Рейнольдса, Прандтля и геометрических характеристик в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) на базе 4-слойной модели турбулентного пограничного слоя, показавшее довольно адекватное согласование разработанной теории с имеющимся экспериментальным материалом.
5. ОСНОВНЫЕ ВЫВОДЫ
Разработана математическая теоретическая модель для расчётов и получены аналитические зависимости для интенсифицированной теплоотдачи при турбулентных течений в поперечно обтекаемом коридорном пучке труб со сплошными плавниками (мембранами) на основе 4-слойной модели турбулентных пограничных слоёв как зависимость от геометрических характеристик каналов и режимов течений теплоносителей.
Получены расчётные результаты для интенсифицированной теплоотдачи в плоском канале с двумя симметричными турбулизаторами как зависимость от определяющих характеристик, которые очень хорошо согласуются с имеющимися экспериментальными материалами, но имеющие перед опытными данными определённое преимущество, так как допущения, принятые при их выводах, распространяются на гораздо более широкий диапазон определяющих характеристик, нежели ограничения, наложенные на опытные данные.
Теорию необходимо использовать для расчёта теплообмена некоторых каналов проточной части теплообменных аппаратов и устройств, образующихся в поперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранные поверхности нагрева, мембранные теплообменные аппараты).
По результатам расчётов на основе разработанной четырёхслойной модели турбулентного пограничного слоя можно осуществлять оптимизацию интенсификации теплообмена в поперечно обтекаемом коридорном пучке труб с непрерывными плавниками (мембранами) на базе 4-х-слойной модели турбулентного пограничного слоя, а также управлять данным процессом интенсификации теплообмена.
Практическое применение мембранного коридорного пучка состоит в качестве ширмовых элементов водяных экономайзеров и промежуточных пароперегревателей, в теплонасосных отопительных системах, в авиации - в системах кондиционирования воздуха (СКВ).
1. Эффективные поверхности теплообмена / Э.К.Калинин, Г.А. Дрейцер, И.З.Копп, и др. — М.: Энергоатомиздат, 1998. — 408 с.
2. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах. — М.: Машиностроение, 1972. — 220 с.
3. Величко В.И., Пронин В.А. Расчёт теплоотдачи в плоском канале с отрывом и присоединением воздушного потока // Межвузовский тематический сборник научных трудов № 54. Интенсификация тепломассообмена в энергетических установках. — М.: МЭИ, 1985. — С. 84—91.
4. Мигай В.К., Фирсова Э.В. Теплообмен и гидравлическое сопротивление в пучках труб. — Л.: Наука, 1986. — 195 с.
5. Лобанов И.Е., Мякочин А.С., Низовитин А.А. Моделирование интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами на базе уравнения баланса турбулентной пульсационной энергии // Вестник МАИ. — 2007. — Т. 14. — № 4. — С. 13—22.
6. Эффективность использования в котлах мембранных конвективных и ширмовых поверхностей нагрева / В.А.Локшин, И.Д.Лисейкин, И.А.Сотников и др. // Теплоэнергетика. — 1973. — № 6. — С. 43—48.
7. Локшин В.А., Лисейкин И.Д. Исследование и расчёт теплоотдачи мембранных конвективных поверхностей нагрева // Теплоэнергетика. — 1971. — № 2. — С. 36—40.
8. Локшин В.А., Лисейкин И.Д. Исследование и расчёт аэродинамики мембранных конвективных поверхностей нагрева // Теплоэнергетика. — 1971. — № 9. — С. 35—37.
9. Локшин В.А., Мочан С.И., Фомина В.Н. Обобщение материалов по аэродинамическим сопротивлениям шахматных поперечно омываемых пучков труб // Теплоэнергетика. — 1971. — № 10. — С. 67—70.
10. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах: Диссертация на соискание учёной степени доктора технических наук. — М., 2005. — 632 с.
11. Дрейцер Г.А., Лобанов И.Е. Моделирование теплообмена в кольцевых каналах с турбулизаторами с помощью семислойной модели турбулентного пограничного слоя // Доклады Академии Наук. — 2005. — Т. 402. — № 2. — С. 184—188.
12. Лобанов И.Е. Моделирование теплообмена в кольцевых каналах с турбулизаторами с помощью семислойной модели турбулентного пограничного слоя // Проблемы газодинамики и тепломассообмена в энергетических установках: Труды XV Школы-семинара молодых учёных и специалистов под руководством академика РАН А.И.Леонтьева. — М.: МЭИ, 2005. — T.1. — С. 103—106.
13. Dreitser G.A., Myakotchin A.S., Lobanov I.E. A simple method for evaluation of heat transfer enhancement in tubular heat exchangers under single-phase flow, boiling, condensation and fouling conditions // Proceeding of the Third International Conference on Compact Heat Exchangers and Enhancement Technology for the Process Industries held at the Davos Congress Centre. — Davos (Switzerland), 2001. — P. 445—455.
14. Dreitser G.A., Myakotchin A.S., Lobanov I.E. Effective Heat Transfer Enhancement in Tubular Heat Exchangers under Single–Phase Flow, Boiling, Condensation and Fouling Conditions // International Journal of Heat Exchangers. — 2002. — V. III. — № 3. — P. 105—127.
15. Лобанов И.Е. Моделирование теплообмена и сопротивления при турбулентном течении в каналах теплоносителей в условиях интенсификации теплообмена // Труды Третьей Российской национальной конференции по теплообмену. В 8 томах. Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. — М.: МЭИ, 2002. — С. 140—143.
16. Дрейцер Г.А., Лобанов И.Е. Исследование предельной интенсификации теплообмена в трубах за счёт искусственной турбулизации потока // Теплофизика высоких температур. — 2002.— Т. 40. — № 6. — С. 958—963.
17. Дрейцер Г.А., Лобанов И.Е. Моделирование изотермического теплообмена при турбулентном течении в каналах в условиях интенсификации теплообмена // Теплоэнергетика. — 2003. — № 1. — С. 54—60.
18. Dreitser G.A., Lobanov I.E. Modelling of Heat Transfer and Hydraulic Resistance of Turbulent Gas and Liquid Flow in Tubes with Circular Turbulizers // Proceeding of the Fourth International Conference on Compact Heat Exchangers and Enhancement Technology for the Process Industries held at the Fodele Beach Hotel. — Crete Island (Greece), 2003. — P. 139—147.
19. Дрейцер Г.А., Лобанов И.А. Моделирование предельной интенсификации теплообмена в трубах за счёт искусственной турбулизации потока для различных теплоносителей с постоянными и переменными теплофизическими свойствами // Тезисы докладов и сообщений V Минского международного форума по тепломассообмену. — Минск, 2004. — Т. 1. — С. 67—69.
20. Дрейцер Г.А., Лобанов И.А. Моделирование предельной интенсификации теплообмена в трубах за счёт искусственной турбулизации потока для различных теплоносителей с постоянными и переменными теплофизическими свойствами // Труды V Минского международного форума по тепломассообмену. — Минск, 2004. — Т.1. — № 27. — С. 1—9.
21. Доценко А.И., Максимов Д.А., Лобанов И.Е. Математическое моделирование теплообмена при турбулентном течении в кольцевых каналах с турбулизаторами на внутренней трубе с применением семислойной модели турбулентного пограничного слоя // Современные проблемы науки и образования. — 2009. — № 4. — С. 122—133.
22. Новиков И.И., Воскресенский К.Д. Прикладная термодинамика и теплопередача. — М.: Госатомиздат, 1961. — 548 с.
23. Новиков И.И., Воскресенский К.Д. Прикладная термодинамика и теплопередача. — М.: Атомиздат, 1977. — 349 с.
24. Локшин В.А., Лисейкин И.Д., Аронов Д.И. Исследование и расчёт теплоотдачи и аэродинамических сопротивлений мембранных коридорных пучков труб. — Теплоэнергетика. — 1975. — № 11. — С. 75—77.
25. Лисейкин И.Д., Джанелидзе M.М. Исследование теплоотдачи и аэро¬динамического сопротивления в поперечно-омываемых мембранных шахматных пучках труб. — Теплоэнергетика. — 1982. — № 9. — С. 63—67.
26. Лисейкин И. Д. Теплоотдача и аэродинамическое сопротивление мембранных конвективных поверхностей нагрева. — Теплоэнергетика. — 1984. — № 12. — С. 66—70.
27. Мигай В.К., Быстров П.Г., Моргун А.В. Исследование локальной теплоотдачи конвективных мембранных поверхностей нагрева котлов. — Теплоэнергетика. — 1982. — № 10. — С. 43—46.
28. Мигай В.К., Быстров П.Г., Моргун А.В. Исследование локального конвективного теплообмена в мембранных пучках труб парогенераторов. — Труды ЦКТИ. — 1982. — Вып. 192. — С. 14—20.
29. Леньков Ю.А., Назаренко В.С, Моргун А.В. Теплообмен в мембранных конвективных коридорных пучках. — Труды ЦКТИ. — 1982. — Вып. 192. — С. 27—33.
30. Конвективный теплообмен и температурный режим мембранного экономайзера / А.Ю.Вески, А.И.Гольдберг, А.М.Копелиович и др.. — Энергомашиностроение. — 1979. — № 12. — С. 9—11.
31. Мигай В.К. Моделирование теплообменного энергетического оборудования. — Л.: Энергоатомиздат. Ленинградское отделение, 1987. — 263 с.
32. Lobanov I.E., Stein L.M. Theory of intensified heat exchange in turbulent flow reattachment areas in tubes with turbulators // Университетский научный журнал. — 2014. — № 8. — С. 77—90.
Рецензии:
30.09.2020, 21:16 Мирмович Эдуард Григорьевич
Рецензия: Все работы Игоря Евгеньевича, как и настоящая, обладают всем набором признаков научности и практической ценности, отвечают требованиям научной публицистики. Она безусловно рекомендуется к печати в двух вариантах. Либо в представленном виде, либо, по усмотрению автора, с учётом робких замечаний рецензента.
Желательно не сразу работу представлять в 4 автономных статей, а что-то впереди обобщающее сказать в виде введения.
Желательно в заключении уточнить конкретику: не просто получены аналитические выражения, а добавить: "в которых в отличие от полученных ранее..." или ещё что-то конкретное. Чуть-чуть. А то в аннотации мы узнали, что созданы модели и получены соотношения, и в заключении то же самое. А надо что-то узнать, не читая и не изучая всю работу.
Просмотреть описки типа: "Лок-шин", "критерий Нуссельта равно", "разработаноа" и др.
Комментарии пользователей:
|
15.10.2020, 23:21 Лобанов Игорь Евгеньевич Отзыв: Я исправил имеющиеся недостатки, связанные с опечатками и т.д., и т.п. Я добавил конкретные приложения для данного вида теплообменных аппаратов. Относительно того, как полученные решения отличаются от предыдущих, то могу сказать, что ранее на данную тему результаты по теплообмену ещё не были получены. Я добавил несколько слов о том, чем данное решение отличается от ранее полученных решений для плоских каналов. |
|
16.10.2020, 8:19 Галкин Александр Федорович Отзыв: Любопытно наблюдать постоянный многолетний диалог между И.Е.Лобановым и Э.Г.Мирмовичем. Неужели г-ну Мирмовичу не понятно, что автор пишет эти "статьи" исключительно для себя и никто из специалистов их не читает. Найдите хотя бы одну ссылку на любую публикацию автора в этом журнале. Их НЕТ!!! И не будет. Как раз из-за того. что они "обладают всем набором признаков научности и практической ценности", но только признаками! |
Оставить комментарий
Вверх