Разделы: Математика
Размещена 22.04.2024. Последняя правка: 01.05.2024.
Просмотров - 203

МАТЕМАТИЧЕСКИЕ СКАТЕРТИ. ИССЛЕДОВАНИЕ ПРОСТЫХ ЧИСЕЛ И ЧИСЛОВЫХ РЯДОВ

Соловьёв Виктор Григорьевич

ООО "Бизнескоп Консалтинг"

Математик-программист

УДК 511

Введение. Изучение математиками простых чисел в части поиска закономерностей их распределения известно с древнейших времен. Конечной целью такого изучения является доказательство того, что кажущийся хаос распределения простых чисел - всего лишь наше недопонимание каких-то общих законов математики и природы в целом. Поэтому подобные задачи никогда не теряют свой актуальности, каждой раз приближают нас с помощью новых открытий к пониманию математической общности.

С помощью современной компьютерной техники программистам-математикам удалось значительно продвинуться в использовании графических методов изучения поведения простых чисел на координатной плоскости. Суть таких методов сводится к визуальному и аналитическому восприятию графических паттернов при размещении на плоскости по заданным координатам точек огромного количества простых чисел. В первую очередь, этому способствовало открытие знаменитым ученым, кстати не математиком (!), Станиславом Уламом, так называемой, математической скатерти [2], состоящей из прямоугольных витков спиралей и размещением на ней простых чисел. Удивительно, но другой знаменитый ученый, Роберт Сакс (тоже не математик!), продолжил изучение простых чисел, открыв математическую скатерть в виде архимедовой спирали [5].

Теория математической скатерти. Если последовательно расположить числа натурального ряда, начиная с единицы, по закрученной против часовой стрелки спирали, как показано на рисунке 1а, а потом оставить на ней только простые числа (рисунок 1б), то можно заметить определенную закономерность их расположения по диагональным прямым.

 

Особенно это хорошо видно при огромном числе простых чисел, нанесенных в виде точек на скатерть Улама (см. рисунок 1в). Рассмотрим скатерть Улама, в дальнейшем U-скатерть (в терминологии автора работы), не в виде спирали, но в виде концентрических колец квадратной формы, как показано на рисунке 2.

С учетом того, что любое число на U-скатерти расположено в клетке с номером равным самому числу, выделим прямую и обратную задачи, относящиеся к теории U-скатерти. Первая (или прямая) задача состоит в определения прямоугольных координат для любого числа-клетки на U-скатерти, а именно:

координаты X и Y с номером N клетки, выражающим натуральное число, на U-скатерти вычисляются по формулам

                                                                                             

 

где U – номер кольца U-скатерти (единица расположена на нулевом кольце, числа 2 -9 расположены на 1-ом кольце, числа 10 – 25 расположены на 2-ом кольце и т.д.)

                              

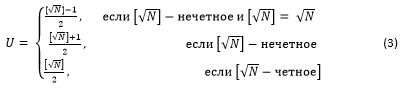
Q – номер четверти кольца U-скатерти

Квадратные скобки означают вывод целой части числа.

Каждая четверть кольца включает числа в заданном диапазоне и начинается с числа большего на единицу от углового и заканчивается ближайшим последующим угловым числом. Например, первая (правая или восточная) четверть кольца с номером 4 включает числа из диапазона 50 ÷ 57, вторая (ве            рхняя или северная) четверть - 58 ÷ 65, третья (левая или западная) четверть - 66 ÷ 73, и, наконец, четвертая (нижняя или южная) четверть - 74 ÷ 81.

Вторая (или обратная) задача состоит в определении числа или номера клетки на U-скатерти по заданным координатам. Тогда,

номер N клетки на U-скатерти по известным координатам X и Yвычисляется по формулам

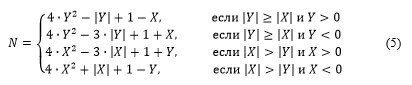
Прямые скобки означают вывод числа по модулю.

Рассмотрим пример вычислений кординат по прямой задаче. Пусть имеем число N = 97, кстати это простое число. Требуется вычислить его прямоугольные координаты. По формуле (3) вычисляем номер кольца U и получаем 5. По формуле (4) вычисляем четверть кольца Q и получаем 2. Подставляя параметры U и Q в уравнения (1) и (2) получаем, что X = -1, а Y = 5.

Рассмотрим пример вычислений по обратной задаче. Пусть имеем значения координат X = -1, Y = 5. Требуется вычислить клетку-число N. По условиям формулы (5) заданные координаты соответствуют первой строке. Тогда, N = 4 * 5^2 – 5 + 1 – (-1) = 97. Метод вычислений становится особенно эффективным при очень больших значениях N, с которыми мы будем иметь дело в дальнейших наших рассуждениях.

Также отметим дополнительно некоторые свойства колец:

- число клеток (чисел) Ku на каждом кольце U определяется формулой

- максимальное число  Nmax, расположенное на кольце с номером U равно

- минимальное число Nmin, расположенное на кольце с номером U равно

- каждое последующее кольцо U содержит число клеток-чисел на 8 больше предыдущего.

Конечно, существуют и другие методы вычислений координат, в частности,  L-метод или Turtle-метод [3], согласно которому используется управление рисованием в полярной системе координат, связанной с текущим положением роботоподобного устройства (черепахи). Однако, в отличие от него, приведенные выше формулы, позволяют выполнять вычисления для любой отдельно стоящей клетки независимо от положения других чисел. 

Теория математической скатерти Сакса. Для последующих сравнений выделим также математическую скатерть Сакса (в терминологии автора работы S-скатерть), на которой натуральные числа расположены (рисунок 3а) последовательно на архимедовой спирали,

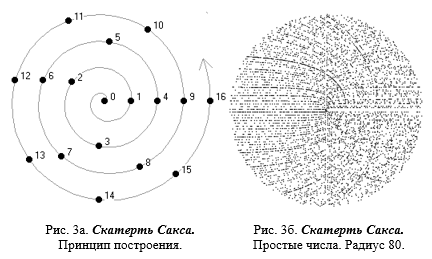
определяемой полярными координатами, связанной с декартовыми прямоугольными координатами следующими соотношениями

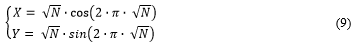
По аналогии со скатертью Улама, Сакс также расположил на спирали только простые числа, получив картину в виде заметных спиральных паттернов (рисунок 3б), являющимися кривыми произведений как множество квадратных уравнений.

Теоретическое обоснование новой модели математической скатерти. Наиболее близкой к оригинальной модели V-скатерти (в терминологии автора работы) является также известная модель, в свое время разработанная автором и изложенная в [4]. Числа на модернизированной V-скатерти расположены следующим образом:

- представим скатерть в виде набора концентрических колец квадратной формы, как показано на рисунке 4

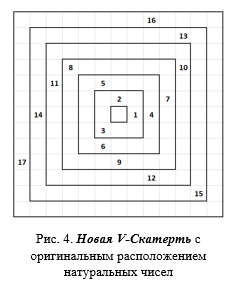
- условно поместим в центр V-скатерти (нулевое кольцо) ноль, не вписывая в скатерть;

- следующее натуральное число (единицу) разместим на V-скатерти, отсчитав от нуля по первому кольцу против часовой стрелке до 1;

- следующее натуральное число (двойку) разместим на V-скатерти, отсчитав от единицы по первому кольцу против часовой стрелки до 2;

- следующее натуральное число (тройку) разместим на V-скатерти, отсчитав от двойки по первому кольцу против часовой стрелки до 3;

- следующее натуральное число (четверку) разместим на V-скатерти, отсчитав от тройки по первому кольцу с переходом на второе кольцо против часовой стрелки до 4;

- аналогично поступаем со всеми последующими натуральными числами, записывая каждый раз натуральное число по кольцам, отстоящего от предыдущего на число клеток, равным следующему числу.

На рисунке 4 на первых 6-ти кольцах уместилось 17 последовательных натуральных  чисел. На первый взгляд, кажется, что бессистемным образом. Однако это не так, что и будет продемонстрировано далее при анализе большого количества данных. Причем результаты окажутся мало прогнозируемыми,  в какой-то мере эвриститическими!

Таким образом, получаем ряд натуральных чисел на V-скатерти, которые более разрежены на плоскости, нежели на U-скатерти или S-скатерти, при этом координаты X и Y любого натурального числа N определяются по формулам (1) и (2) с тем лишь отличием, что в них

Фактически, каждое натуральное число N на V-скатерти расположено в клетке с номером равным сумме чисел по накоплению до N. Вот почему мы так подробно остановились на теории U-скатерти.

Если на U-скатерти на K кольцах расположено количество Ku натуральных чисел

то на V-скатерти на K кольцах расположено количество Vu натуральных чисел

Сравнение и анализ паттернов математических скатертей. Для визуального представления в расположении на математических скатертях различных математических рядов при поиске закономерностей необходимы вычисления координат большого множества чисел. Современные вычислительные средства позволяют выполнить все требуемые для наших задач вычисления. Рассмотрим некоторые математические ряды, расположенные для сравнения на U-скатерти, S-скатерти и V-скатерти, главное внимание уделив, конечно же, ряду простых чисел.

Ряд натуральных чисел (1, 2, 3, …) приведен на рисунках  5а, 5б и 5в соответственно на U-S-Vскатертях

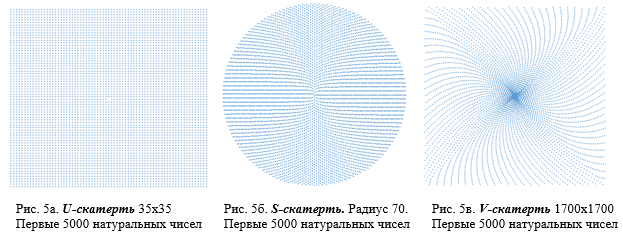
Ряд натуральных четных чисел (2, 4, 6, …) приведен на рисунках 6а, 6б и 6в соответственно на U-S-Vскатертях

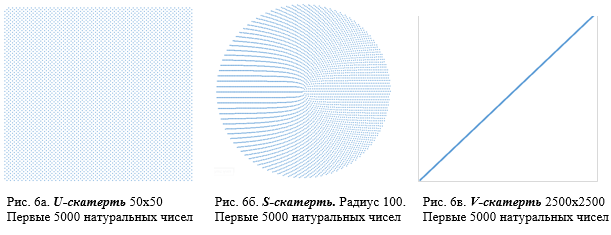
Ряд натуральных нечетных чисел (1, 3, 5, …) приведен на рисунках 7а, 7б и 7в соответственно на U-S-Vскатертях

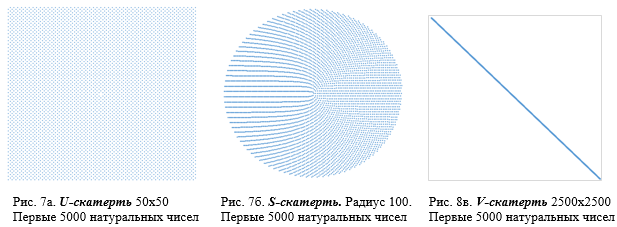
По рисункам 5-7 видно, что в отличие от V-скатерти, числа, расположенные на U-S-скатертях практически неизменны по своим графическим паттернам.

Главный вывод о применимости математических скатертей следующий:

V-скатерть универсальна с точки зрения графических построений числовых натуральных рядов и может быть рекомендована как инструмент исследований в этом качестве.

Вероятно, при исследовании многих других числовых рядов с помощью V-скатерти можно получить интересные результаты. Впрочем, подобные исследования выходят за рамки данной работы и возможны в дальнейшем как продолжение работы.

Переходим к самому примечательному ряду простых чисел (2, 3, 5, 7, 11, 13, 17, 19, 23, …) на V-скатерти, на которой простые числа в зависимости от максимального члена ряда или кольца приведены на рисунках 8а-8г, для наглядности несколько увеличенных в размерах.

 

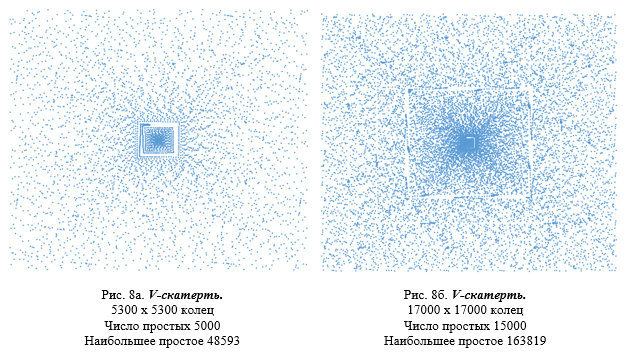
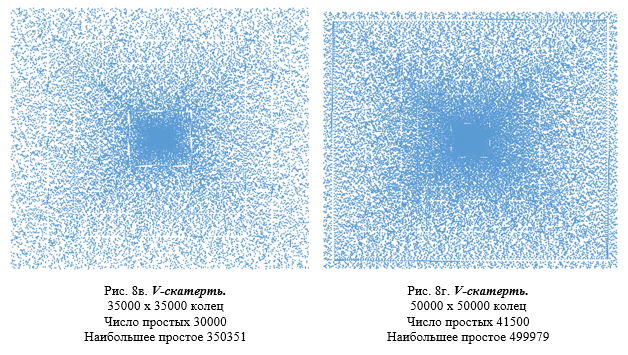
Если на U-скатерти и S-скатерти графические паттерны образуют соответственно диагональные и спиральные области повышенной плотности распределения точек, то на  всех последних рисунках, относящихся к V-скатерти, отчетливо видны графические паттерны в виде квадратов разных размеров практически с нулевой плотностью. Это объясняется тем, что на одной части колец V-скатерти ряд чисел совершают приблизительно один или несколько полных оборотов на кольцах с небольшим смещением, при этом образуя на V-скатерти, видимое прямое и попятное движение, а на другой части V-скатерти  ряд простых чисел совершает один или несколько неполных оборотов, распределяясь более равномерно и случайно на V-скатерти. Поэтому мы и наблюдаем пустые кольца, не занятые простыми числами на V-скатерти.

Причудливость, а может и для кого-то красота узоров (для автора уж точно!), еще больше проявляется, если посмотреть график плотности распределения точек по одной оси, например, оси X, в заданном диапазоне, как показано на рисунке 9, на котором отчетливо видна периодичность “пустых” колец равная приблизительно 2500 кольцам. В частности, первое пустое кольцо, которое проявилось в районе 500-го кольца (см. рисунок 8а), имеет ширину около 200 колец (на рисунке 9 видна как маленькая зазубринка слева)

 

Еще одной особенностью распределения простых чисел на V-скатерти является то, что отношение Z значения простого числа P к номеру кольца U, как показано на графике (рисунок 10)

 

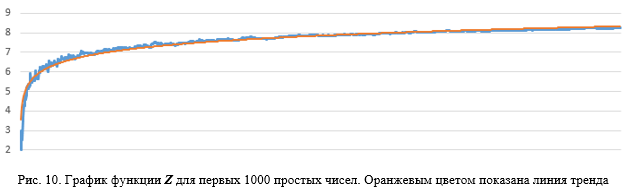
подчиняется определенному не случайному закону и оценивается формулой

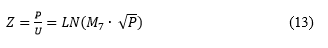
в которой M₇ = 127 – число Мерсенна [1].

Безусловно, вариантов рассмотрения положений ряда простых чисел на V-скатерти можно продолжать до бесконечности. Авторские исследования только в начале пути, о чем свидетельствует данная работа. Продолжение следует...

Выводы. Распределенностью простых чисел на числовой оси или математической скатерти занимаются многие математики с целью доказать отсутствие хаоса в ряде простых чисел. Анализ поведения простых чисел на оригинальной V-скатерти - лишнее тому доказательство, позволяющее открыть новые законы в теории чисел.

1. Brent R.P., Zimmermann P. Random number generators with period divisible by a Mersenne prime // Lecture Notes in Computer Science. 2003. Т. 2667. С. 1-10.
2. Гарднер M. Простые числа // Математические досуги. — М.: Мир, 1972. С.413-417.
3. Николов Р., Сендова Е. Начала информатики. Язык Лого / Под ред. Б. Сендова, Пер. с болг. Под ред. А. В. Гиглавого. М.: Гл. ред. физ.-мат. лит., 1989.
4. Соловьев В.Г. Решето Хаоса. LAP LAMBERT Academic Publishing RU. C. 42 -47.
5. Спираль Сакса. [Электронный ресурс]. Режим доступа: https://numberspiral .com/ (дата обращения: 16.04.2024).

Комментарии пользователей:

Оставить комментарий