Статья опубликована в №9 (май) 2014
Разделы: Математика
Размещена 20.05.2014. Последняя правка: 19.05.2014.
Просмотров - 3389

К вопросу о математической модели вселенной и измерениях. Новое в понятии «бесконечность»

Ганичева Наталия Владимировна

numero 1 etude Paris

professeur maths

УДК 51-71

Одной из целей статьи является понятие описываемого феномена простыми школьниками, поэтому автор использует доступный язык без сложных математических терминов. 

Вспомним всем известную координатную плоскость с осями OX, OY , и  центром О - начале координат.

Еще со школьных времен все мы привыкли к определенному восприятию знака бесконечности. Нас учили, что числовая прямая удаляется вправо, - к плюс, и влево, - к минус бесконечности. Таким образом, мы привыкли представлять, что бесконечностей несколько, как показано на рисунке 1:

На ваше внимание выносится модель координатной плоскости, объединяющая классическую и сферическую, где все бесконечности замыкаются в одну. Ее автор, Ганичева Наталия Владимировна , учитель математики предлагает принять, что бесконечность одна, но к ней можно подойти с разных сторон и по разным осям, как показано на рисунке 2.

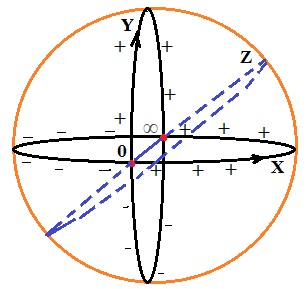
Описание рисунка:

Перед нами точка О, начало координат. Вправо идут числа с плюсом, влево - с минусом. Ось ОХ замыкается в кольцо сзади в точке, называемой бесконечностью и противоположной нулю. Как видим, к ней можно подойти как со стороны положительных так  и со стороны отрицательных чисел. Порядок счета около бесконечности будет :... ∞-1, ∞, ∞ +1 ...

Пример :  ∞-1 +2=∞+1    (раньше подобных примеров не рассматривалось , так как подразумевались  разные бесконечности)

Новшество этой теории заключается в том, что бесконечность в математическом смысле воспринимается не  как неограниченность некоего процесса, а как конкретная точка, неисчисляемая, но конкретная, противоположная нулю и находящаяся на самом дальнем от него расстоянии – на другом полюсе вселенной.

К бесконечности можно подойти и другими путями - по оси ОY (вверх по плюсу и вниз по минусу) и, наконец, по оси ОZ в одну сторону, соединяя точки ноль и бесконечность (сплошная синяя линия), и в другую сторону, соединяя эти же точки, но с внешней стороны обрамленной оранжевым цветом сферы (пунктирная синяя линия).

Теория о замыкании всех бесконечнотей в одну ведет нас к совершенно конкретному видению модели вселенной.

Казалось бы, что прямой путь внутри сферы самый короткий,  но это не так. Следует исходить из того, что все расстояния по всем осям одинаковы.  Чтобы это понять и представить, мы должны ввести понятие «искривление пространства». Длина синей сплошной линии на рисунке (внутри сферы) равна длине синей пунктирной линии (снаружи сферы). И хотя по рисунку этого не видно, представлять этот феномен - значит найти ключ к понятию кривизны трехмерного пространства.

Как видим, мы используем все пространство рисунка - и снаружи, и внутри сферы, представляя вселенную как сферу, которая вворачивается в себя и выворачивается из себя одновременно. 

Мало того, она вворачивается и выворачивается не по одной оси ОZ, а по всем., распределяя это искривление поровну на все оси. По данной модели мы можем сделать 3 предположения:

- либо общее искривление пространства вселенной равно 360°, и при распределении на все оси мы получим  по 120° искривления на ось, или по 60° на каждое  направление.,

- либо искривление пространства по каждой оси равно 360°, то есть общее искривление пространства вселенной равно 1080°.

- либо общее искривление пространства вселенной равно 360°, и искривления по всем осям независимы, то есть по каждой оси оно тоже будет составлять 360° . (Теории на проверку)

Несколько слов об измерениях. Нужно определится с этим понятием. Измерения - это миры, где все меры находятся на порядок или несколько порядков выше или ниже от наших. Назовем наше измерение «декаизмерением», где размеры соответствуют  10¹ – мы меряем расстояния метрами, массу килограммами, силу тока амперами.

Измерение же, в котором живут насекомые (такие как муравьи или мушки дрозофилы) - является на порядок ниже нашего, назовем его «миллиизмерением». В нем все примерно в 1000 раз меньше, чем в нашем: насекомые составляют несколько миллиметров., весят несколько миллиграмм, общаются на ультразвуке, чья частота выше нашей в тысячу раз (если наш верхний предел около 20 тысячь герц, то их - примерно 20 миллионов герц). Автор считает, что, следуя такой динамике, логично предположить, что и остальные важные меры отличаются от наших в тысячу раз: сила тока, время, термодинамическая температура, колличество вещества и сила света.

Развиваем идею об измерениях: следующим после «миллиизмерения» идет «микроизмерение», где все меры в миллион раз отличаются от наших. В этом измерении господствуют существа размера микроба. Затем идет «наноизмерение», где живут молекулы. Надо отметить, что это очень интересное измерение – в нем скорости могут быть настолько  велики, что время может останавливаться. В качестве примера можно сказать, что время жизни стабильной молекулы водорода бесконечно. С другой стороны, если произойдет событие, при котором молекула переходит из стабильного состояния в другое (например смещение электрона), то время ее жизни может укоротиться до наносекунд. Изучение наноизмерения принесет нам много открытий.

Затем идет «пиктоизмерение», или 10 в минус 12 степени, где господствуют кварки и бозоны и т.д.

Автор этой теории не исключает, что более дальние измерения населены суббозоновыми частицами, чья масса и размер отрицательны. Если в нашем измерении вселенная расширяется, то в измерениях с размерами от 10 в минус 26 степени  вселенная сужается.  Во всяком случае, наука уже доказала, что если плотность материи меньше критического значения  10 в минус 26 степени , то кривизна пространства отрицательна.

Говоря о макроизмерениях, можно  отметить сначала мир, населенный созданиями , меряющими расстояния километрами и весящими тонны – здесь мы говорим о климатических явлениях - ураганах, землетрясениях и тп. После «килоизмерения» идет «мегаизмерение» , населением которого являются планеты, затем «гигаизмерение», где царствуют галактики и т.д.

Надо сказать, что следуя данной модели вселенной, мы можем наблюдать только ее половину, только часть, которая расширяется. Возможно, что  на уровне «петаизмерения» 10¹⁵ вселенная снова начинает сужаться, но это в принципе не важно - важна закономерность: вселенная делится на определенное колличество измерений, в половине из которых она выворачивается из себя, а в другой половине сворачивается.

Следует отметить, что нами рассматривались только измерения по параметру «физические меры» (размер, вес, колличество вещества), но параметров может быть несколько , и они зависят от разных видов материи и энергии. Все измерения по параметру физических мер замыкают вселенную в круг (пусть это будет ось OZ), а все измерения по всем возможным параметрам мер будут замыкать ее в сферу. Автор данной теории не исключает, что такой феномен, как «душа», (определяемый автором как особое энергетическое поле, содержащее полную информацию о всех актах, мыслях и чувствах его ностителя) является жителем одного из таких измерений.

Автор этой теории считает, что ни один феномен, открытый до сегодняшнего дня не противоречит такой модели.

Утверждение того, что вселенная расширяется не противоречит данной модели, так как вселенная действительно расширяется в нашем измерении и во всех измерениях, какие мы способны наблюдать. Данная модель предполагает, что «большой взрыв», который считается началом вселенной , является лишь моментом, при котором наша вселенная начала расширятся, то есть масса вещества перешла критическую точку.

 Данная модель предполагает, что общая энергия вселенной равна нулю . Это значит, что энергия расширения вселенной равна энергии ее сужения.

Что касается времени, то это параметр, показывающий скорость расширения /сужения вселенной. Для жителей каждого измерения оно длится одинаково, но при выходе в другое измерение оно убыстряется или замедляется. (например замедляется в гигоизмерении, убыстряется в миллиизмерении.)

Утверждение о том, что при получении атомной энергии , так же как и при выходе на орбиту Земли наблюдается искривление пространства тоже подтверждает правильность данной модели. Действительно, если базироваться на том, что полное искривление пространства вселенной равно 360°, а вселенная состоит из измерений, то на каждое измерение приходится определенное колличество градусов искривления. Выходя из нашего , «килоизмерения» в «гигоизмерение», на орбиту Земли, мы сохраняем приборы нашего измерения, и они показывают точное искривление пространства, соответствующее разности между нашими измерениями. Исходя из того, сколько градусов составляет это искривление, можно сделать вывод о колличестве измерений по параметру физических мер. (Например, если искривление составляет 1 грудус, то вселенная состоит из 360 измерений по физическим мерам)

Хотелось бы, чтобы классическая математика адаптировала предложенное понятие единой бесконечности и данную модель вселенной, поскольку она проста и обобщает все открытые физические явления.

1. Эйнштейн, А. О специальной и общей теории относительности (общедоступное изложение)Перевод с 12-го изд. под ред. С. Я. Лившица. — М.: Государственное издательство, 1922. — 79 с. — (Популярно-научная библиотека)
2. Damour, Thibault. Le renouveau de la relativité générale (фр.) // La Recherche. — Paris: Financière Tallandier (Sophia Publications), Juin 1987. — Vol. 18. — № 189. — P. 766—776. — ISSN 0029-5671.

Рецензии:

21.05.2014, 8:46 Назарова Ольга Петровна
Рецензия: Интересный материал. Рекомендуется к печати.

5.04.2016, 19:08 Мирмович-Тихомиров Эдуард Григорьевич
Рецензия: Сначала проанализируйте теорему Пифагора на сфере. Она выполнима лишь при микроуглах и параметре контракции (а/2)/sin(а/2), стремящемся к 1. В остальных случаях пространства сумму углов треугольника стремится к 270 град. В общем, всё намного сложнее. Намного. Под вопросом даже 360-градусное,а не стерадианное измерение пространства постоянной кривизны и финдслеровых пространств вообще. И снова неприятно читать "колличество", "растонии" и др. Я против публикации такой статьи со ссылками на популярный сборник или работу 30-летней давности. Не рекомендуется к опубликованию как не соответствующая современному уровню. А Ольгу Петровну уважаю.



Комментарии пользователей:

21.05.2014, 17:15 Любенкова Елена Петровна Отзыв: Очень интересная статья и написана простым доходчивым языком. Данная модель вселенной может объяснить многие современные загадки.

9.06.2016, 22:10 Головорушко Сергей Яковлевич Отзыв: Уважаемая Наталия Владимировна! Я поражен широтой вашей фантазии и кругозора! По модели Вселенной у меня нет слов, а вот по математическому аспекту есть вопрос. Вы, как математик, имеете общее представление о структуре математики как науки. Знаете, когда и зачем вводятся в программу обучения координатные системы. И даже, может быть, знаете, что такое измерения в классическом представлении. В этой связи хочется узнать, в каком месте учебной программы следует начать знакомство с вашей плоско-сферической системой координат и что учитель должен сказать, предваряя знакомство с этой системой? И пару дополнительных вопросов, если можно. Вы задумывались над вопросом, что такое цифры и числа и, если да, то в чем их различие и что означает ноль? И что такое координатная система и оси координат?

9.06.2016, 22:25 Головорушко Сергей Яковлевич Отзыв: Опрометчивые заявления делает Эдуард Григорьевич! Что-то я сильно сомневаюсь, что теорема Пифагора на сфере "выполняется лишь при микроуглах"! Он, похоже, даже не задумался над тем, что сказал. То ли дело Ольга Петровна: "Интересный материал. Рекомендуется к печати." Ни чем материал интересен, ни почему рекомендуется! Не придерешься!

Оставить комментарий