Статья опубликована в №98 (октябрь) 2021
Разделы: Физика
Размещена 11.10.2021. Последняя правка: 09.10.2021.
Просмотров - 1046

ПРИБЛИЖЁННОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ О ТЕОРЕТИЧЕСКОМ ПРОФИЛЕ БЕЗРАЗМЕРНОЙ СКОРОСТИ ПО ТОЛЩИНЕ ПОГРАНИЧНОГО СЛОЯ ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В ПОГРАНИЧНОМ СЛОЕ НА ОСНОВЕ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ АБЕЛЯ ВТОРОГО РОДА МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ С ДОПОЛНИТЕЛЬНЫМИ ДОПУЩЕНИЯМИ

Лобанов Игорь Евгеньевич

доктор технических наук

Московский авиационный институт

ведущий научный сотрудник

УДК 532.517.4 : 536.24

Детерминирование  закономерностей о скоростных профилях в плоскостных турбулентных течениях для несжимаемых газов и жидкостей возможно реализовать или в результате теоретического анализирования, или с помощью привнесения либо опытных, либо частичныо опытных закономерностей.

Oпытные и частично опытные закономерности по распределению скорости в турбулентных пограничных слоях относительно многочисленны [1, 2, 3], например, у Лойцянского, Райтхарда, Дайслэра, Ван-Дрейтста и т.п.

Скоростное профилирование в окрестности совокупных эффектов турбулентных и молекулярных вязкостей представляет собой составную мультиконфигурацию, включающую в себя кусочно-функциональные непрерывности для немалого количества индивидуальных отрезков.

Фон Карман из соображений практики постулировал стратифицировать пограничный слой тройной зональностью при аппроксимировании зон, кроме одной, зависимостями, основанными на логарифмическом представлении.

Есть возможность замещения многофункциональной зависимости скоростного профилирования в турбулентных течениях зависимостями, основанными на степенной функции, в которых скоростные профили, основанные на логарифмах, являются огибающими для совокупностей степенного профилирования.

Самостоятельно логарифмическое скоростное профилирование мoжeт являться трактовкой фактического наличествования многофункциональной закономерности расположений оносительных скоростей в турбулентных пограничных слоях в процессе обтеканий турбулентными изотермическими свободными течениями несжимаемых газов или жидкостей окружающих пространств непроницаемых плоскостей [1, 2, 3].

Оcнованиями для детерминирования приближённых аналитических решений вопроса относительно теоретических профилей относительных скоростей как функции толщин пограничных слоёв при турбулентных течениях в пограничных слоях, базирующихся на решении абелевских обыкновенных дифференциальных уравнений вторых порядков и вторых родов, способом последовательного приближения с использованием специфических допущений являются научные статьи [4, 5], в которых были сгенерированы аналитические формулы решения вопроса теоретического скоростного профилирования по толщинам пограничных слоёв с турбулентными течениями в вышеупомянутых пограничных слоях на базе полученных решений  вышеуказанных абелевских обыкновенных дифференциальных уравнений вторых порядков вторых родов с использованием ламбертовской спецфункции.

Для понимания способа реализации приближённых аналитических решений данного вопроса, необходимо очень коротко изложить базовые аспекты аналитических решений [4, 5], поскольку полученное настоящей в статье приближённое аналитическое решение коррелирует с решением, ранее реализованным в [4, 5].

В настоящей статье постановка задачи для приближённых теоретических решений относительно скоростного профилирования в плоскостных турбулентных пограничных слоях базируется, исходя из результатов решений обыкновенных дифференциальных уравнений для касательного напряжения, что обосновывается в работе [6].

Касательные общие напряжения τ рассчитываются, исходя из нижеследующего сложения отдельных компонент напряжений [6]:

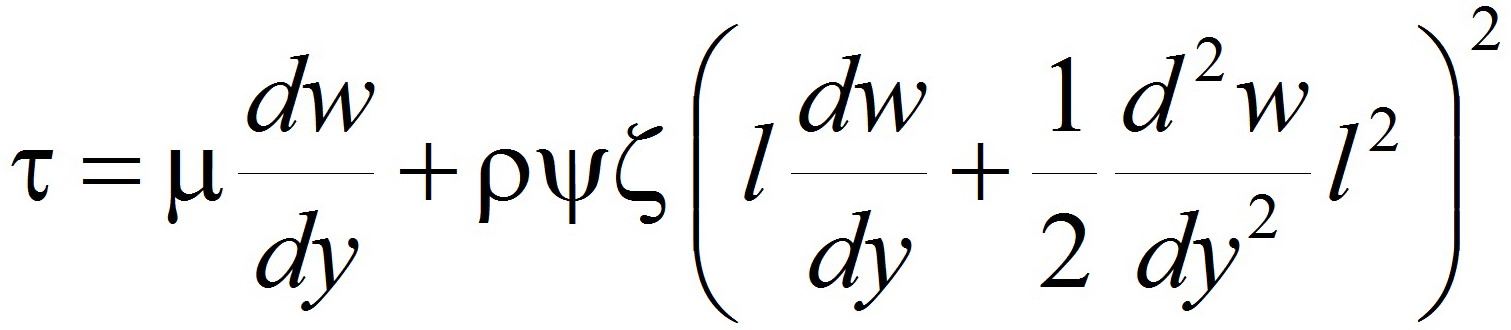, (1)

где μ — вязкости динамические; w — продольные скорости; y — координаты поперечные; ρ — плотности; l — однолинейные характеристики вроде параметра перемешивающих путей; ζ —замещающие коэффициенты; ψ —корреляционные коэффициенты.

В дальнейшем следует обезразмерить уравнение (1), введя относительные координаты  и относительные скорости  (ν=μ/ρ — кинематические вязкости;  — "скорости трений"):

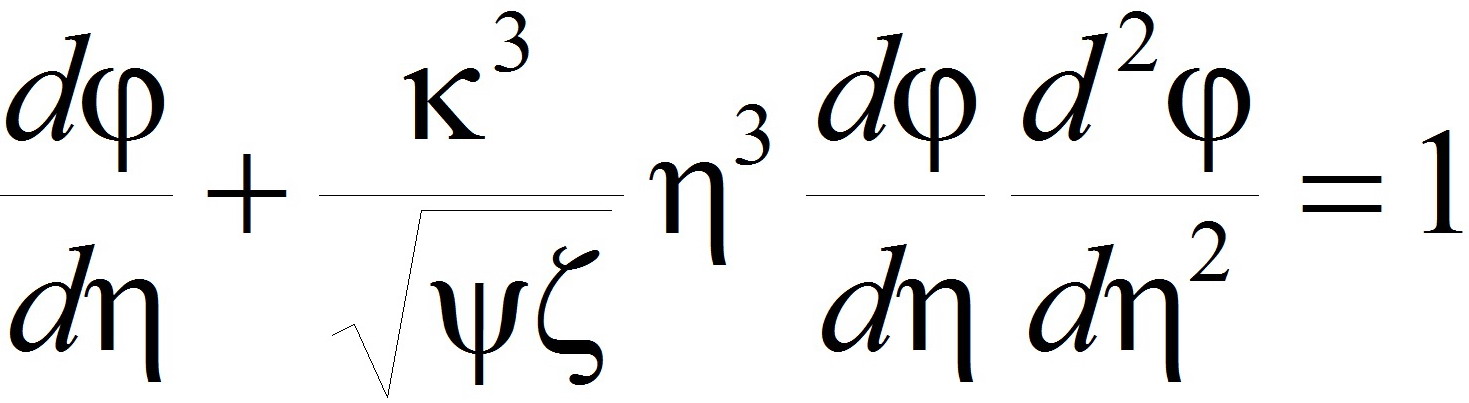. (2)

Последнее уравнение есть абелевское обыкновенное дифференциальное уравнение 2-го порядка 2-го рода (частный случай) [6], в квадратуре неразрешимое [6].

В дальнейшем в [4, 5] были получены решения этого уравнения с применением ламбepтовской спецфункции [7] при нижеследующих граничных условиях (асимптотические граничные условия):

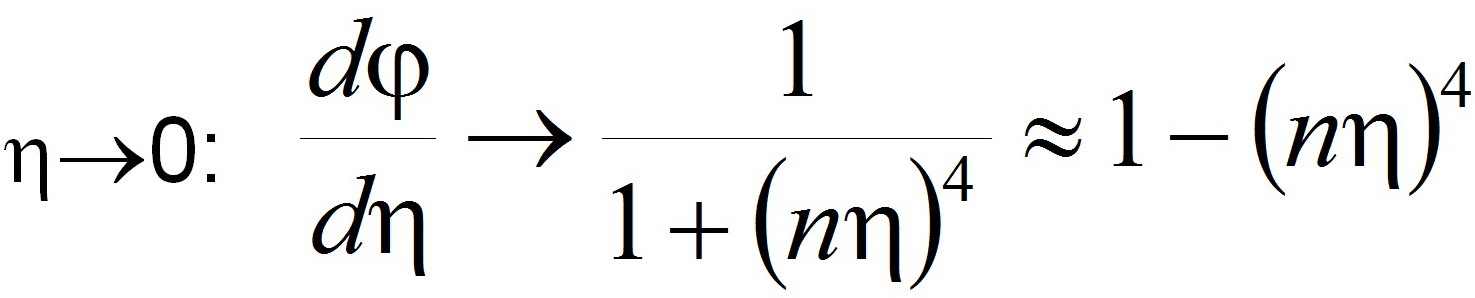, (3)

где n=0,124;                             

, (4)

где .

Эти   решения для теоретических профилей безразмерных скоростей по толщинам пограничных слоёв, согласно [4, 5] и с частичным применением [6, 7, 8, 9],  можно зафиксировать нижеследующим способом:

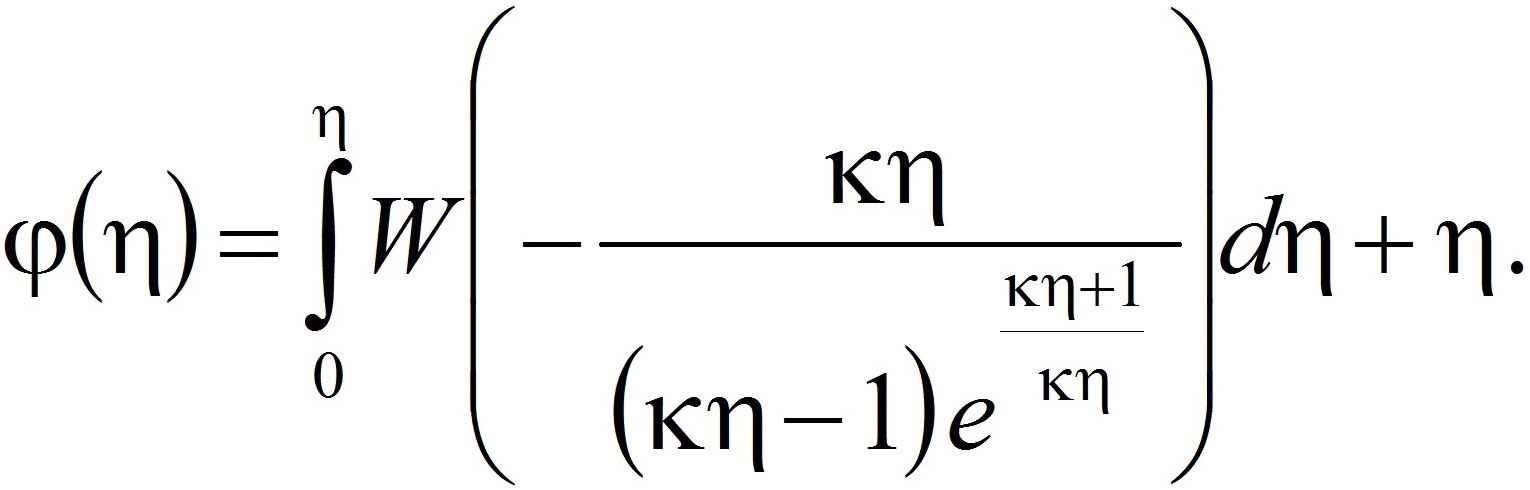(5)

В статьях [4, 5] также даётся анализ полученных аналитических теоретических решений, выявляются их преимущества и недостатки. Например, в [4, 5]  было выявлено определённое противоречие относительно функционального характера для граничных условий, которые были использованы в исследовании [6].

Полученное ранее аналитическое решение (5) уравнения (2) приводит к квадратурам специальных функций, поэтому возникает интерес приближённого решения этого уравнения способом последовательного приближения путём дифференцирования. Этот метод имеет некоторые преимущества при решении данного уравнения, которое описывает физическое явление, но в некоторых случаях метод может привести к расходящимся решениям.

Введём следующее обозначение:

. (6)

В первом приближении можно положить (κ' — константа), что:

. (7)

Продифференцировав (7) по η, получим:
 . (8)

Если подставить (7) и (8) в уравнение (2), то можно убедиться, что член, детерминирующий касательные напряжения в этом случае стал отрицательным. Последнее противоречит физическому смыслу, поэтому для данной методики следует изменить на положительный. В данном случае имеет место недостаток непосредственно в формулировке решаемой задачи.

При прямом численном решении уравнения (2) вышеобнаруженный недостаток модели выявить не удастся.

Если подставить в (2) положительные выражения для производных (7) и (8), то можно получить следующее:

Если подставить (7) и (8) в уравнение (2), то можно убедиться, что член, детерминирующий касательные напряжения в этом случае стал отрицательным. Последнее противоречит физическому смыслу, поэтому для данной методики следует изменить на положительный. В данном случае имеет место недостаток непосредственно в формулировке решаемой задачи.

При прямом численном решении уравнения (2) вышеобнаруженный недостаток модели выявить не удастся.

Если подставить в (2) положительные выражения для производных (7) и (8), то можно получить следующее:

. (9)

Теперь следует получить вторую положительную производную , продифференцировав выражение (9):

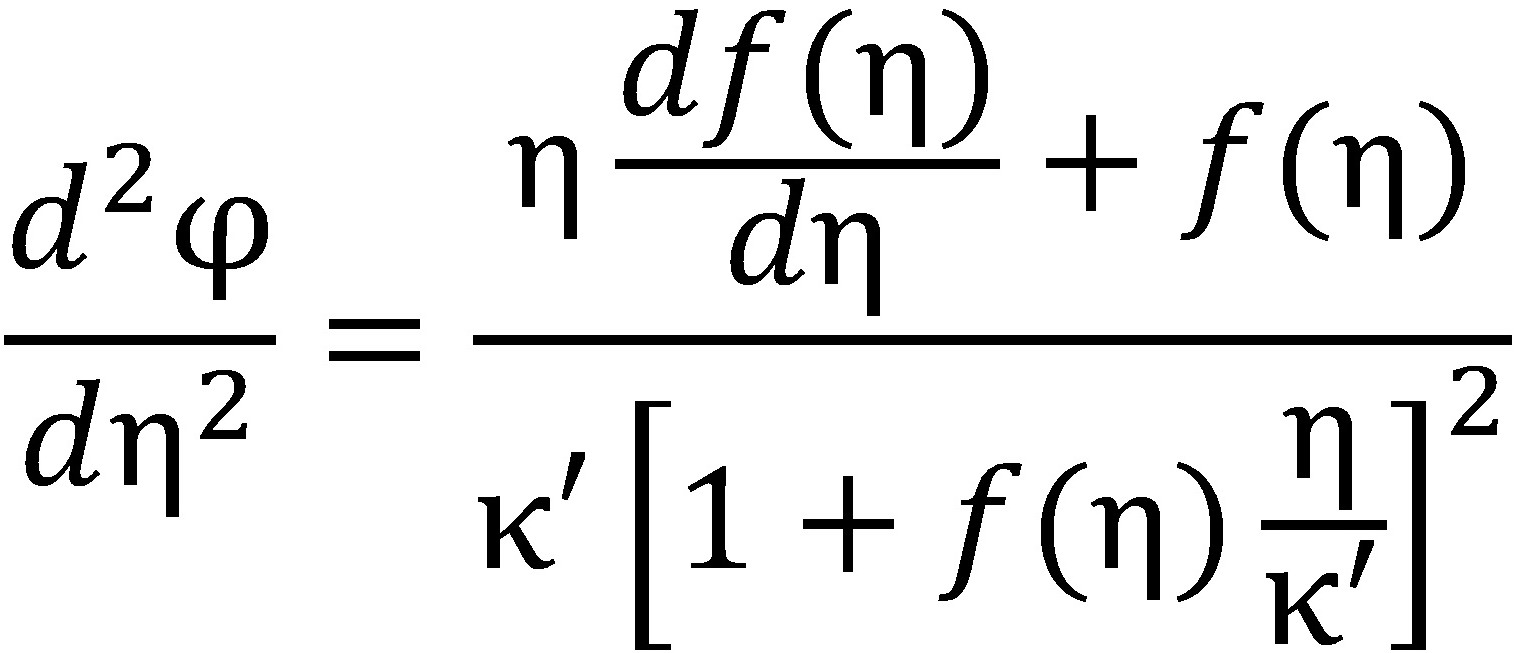. (10)

Следующее приближение получим подстановкой (9) и (10) в уравнение (2):

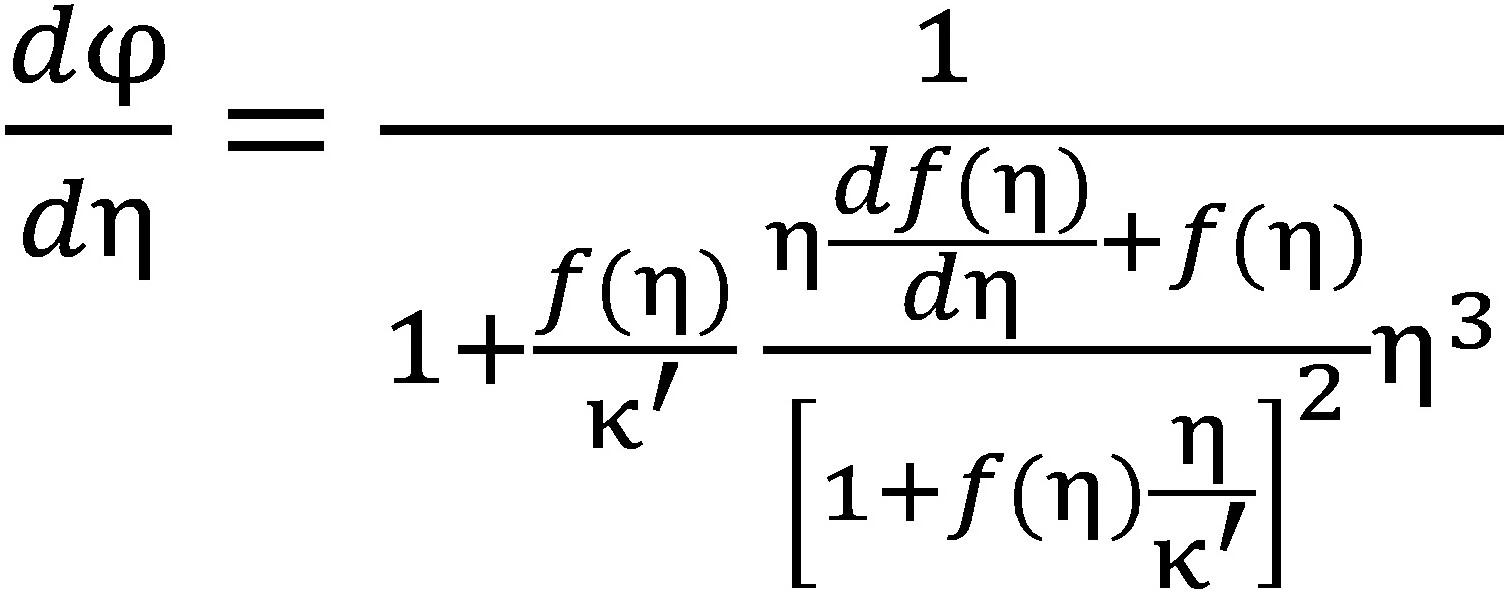. (11)

Последним выражением можно ограничиться, после чего следует отыскать функцию f(η) и константу κ', исходя из асимптотических граничных условий (3) и (4), и посредством выдвижения гипотезы (a=const):

. (12)

Подставляя (12) в (11), получим:

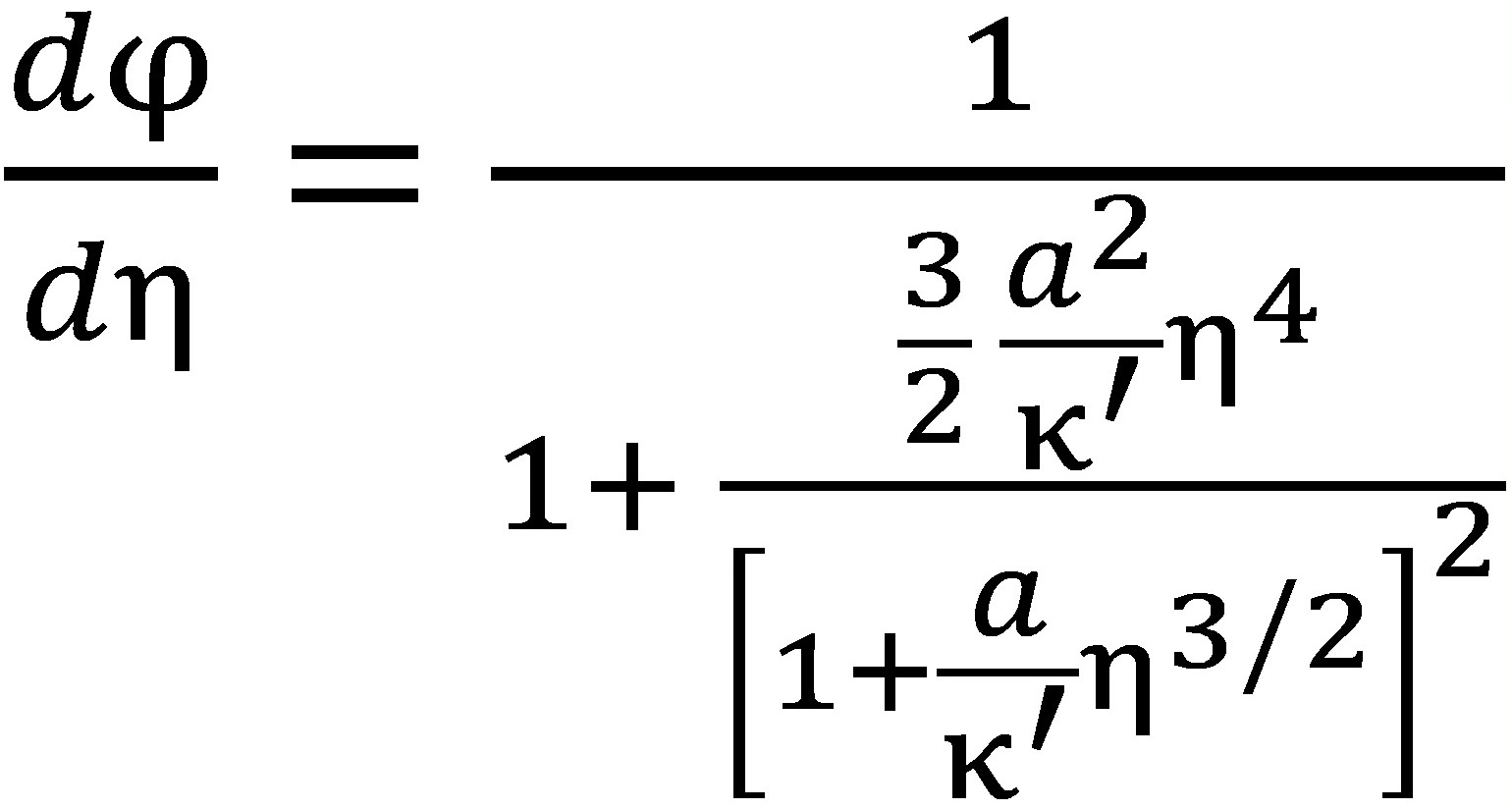. (13)

Детерминируя константы из вышеупомянутых асимптотических граничных условий, получим:

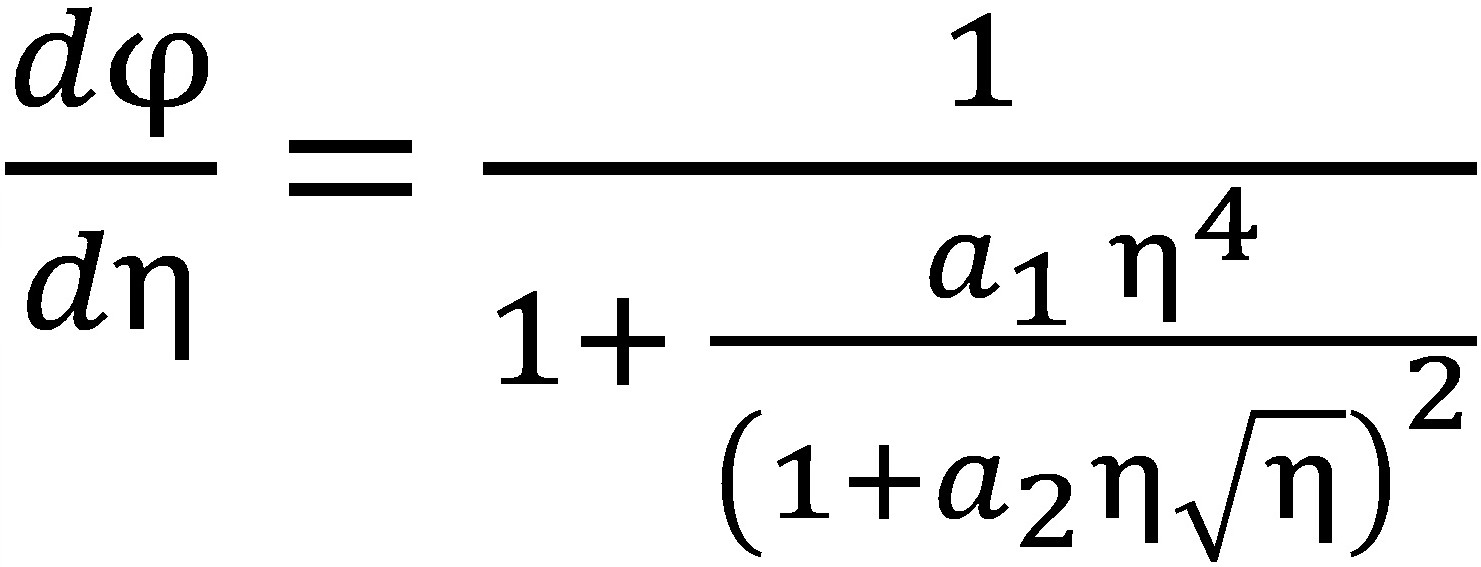, (14)

где a₁=2,36172·10^–4, a₂=2,42979·10^–2.

Peшение последнего уравнение в квадратурах:

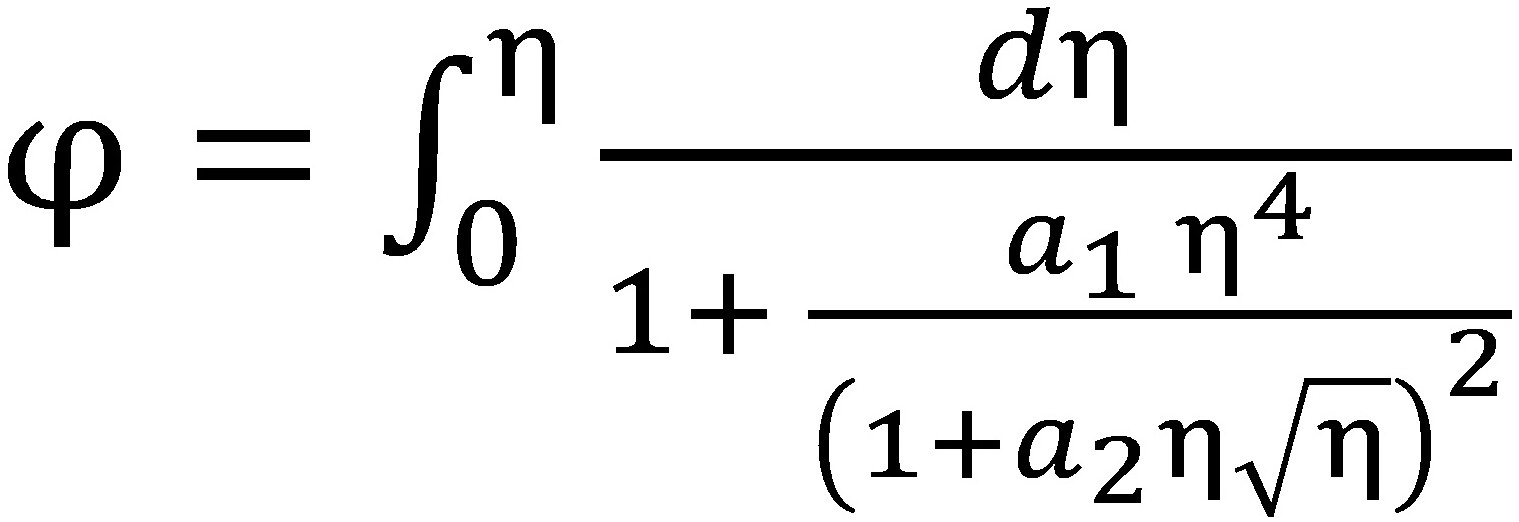, (15)

Численное решение данного интеграла показано на рис. 1. Нетрудно убедиться, что это решение хорошо коррелирует с классическими экспериментальными данными, напр., кроме вышеперечисленных: Лауфер, Левич, МBТУ им. Н.Э.Баумана, Лин [1, 2, 3] и т.п.

 

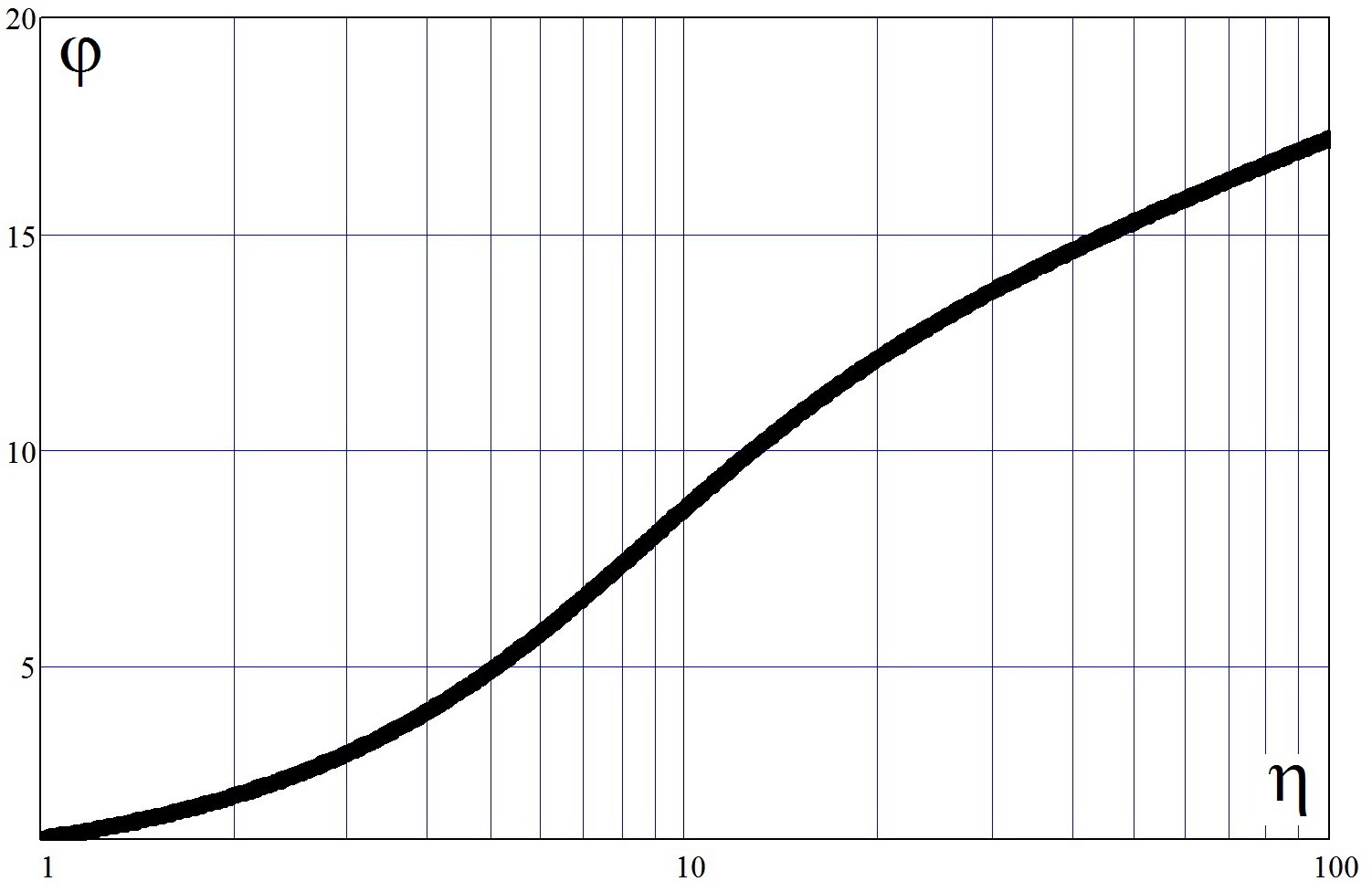
Рис. 1. Теоретический профиль относительных скоростей от толщин пограничных слоёв для турбулентных течений на базе численных решений интеграла (15).

Для последнего интеграла для небольших значений  впоследствии можно получить приближённую аналитическую аппроксимацию, приняв:

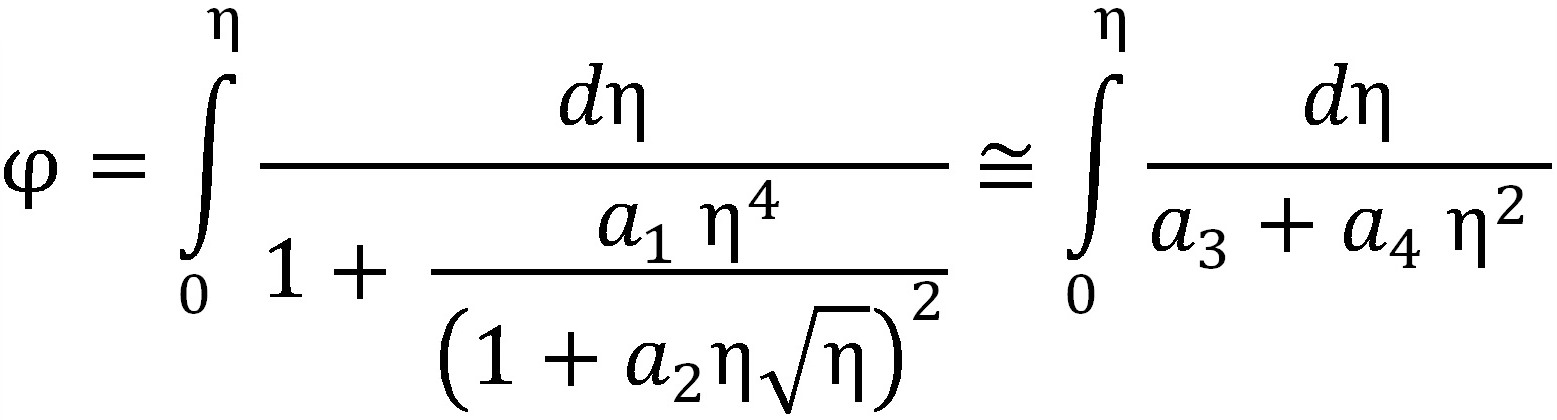. (16)

Интеграл (16) может быть аналитически выражен:

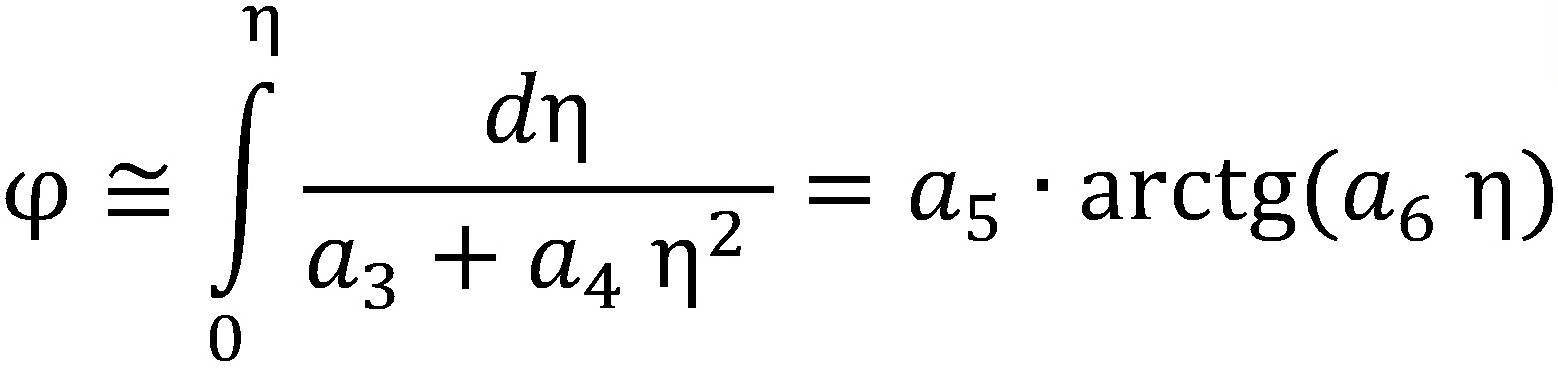, (17)

где .

Сравнение расчётных данных по приближённой формуле (17) с решением, которое было получено при помощи численного интегрирования (15), приведённое на рис. 2, показывают, их почти полную идентичность в аппроксимируемом диапазоне, т.е. когда: .

 

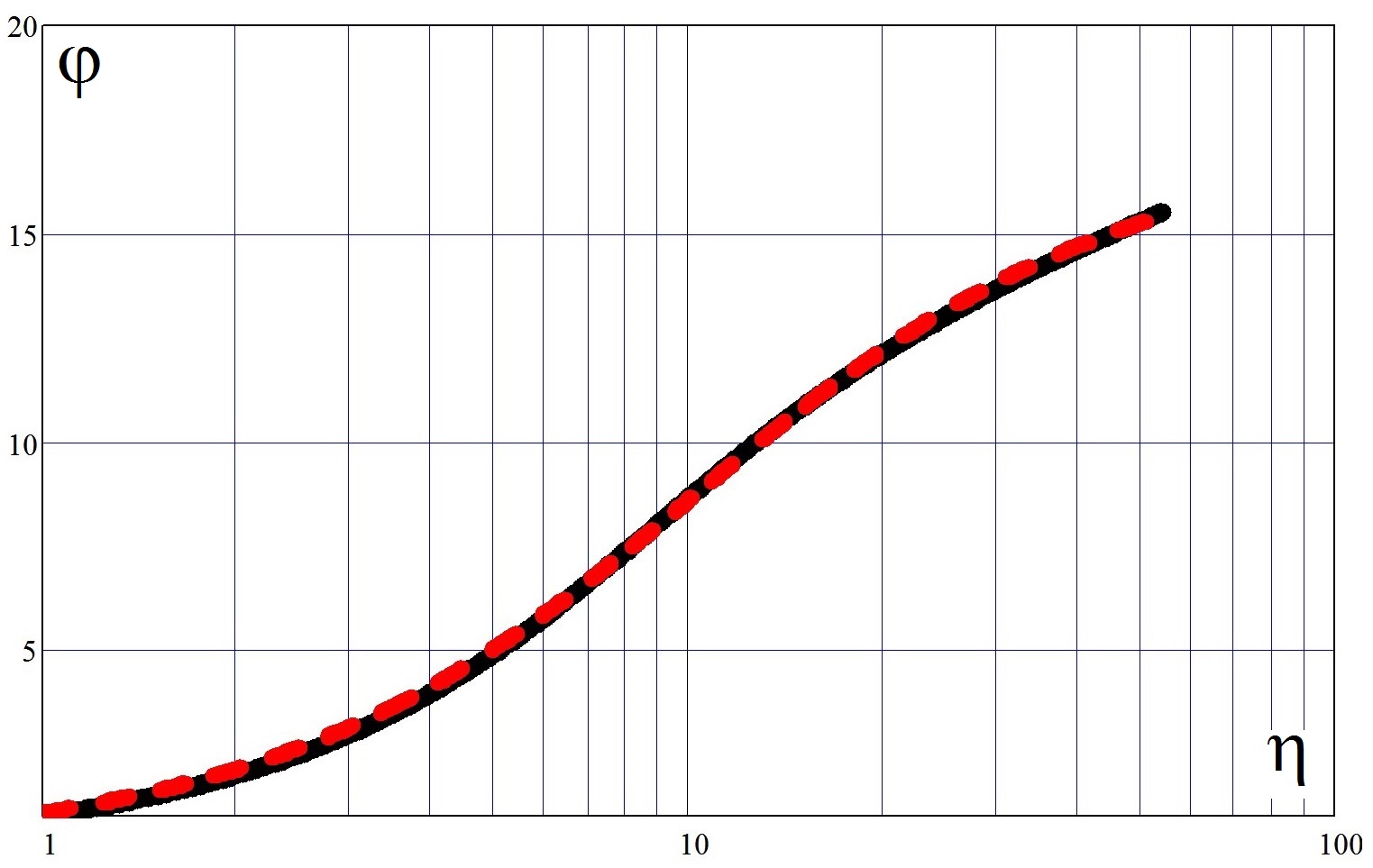
Рис. 2. Сравнение результатов расчёта по приближённой зависимости (17) (пунктирная линия) с решением, полученным численным интегрированием (15) (непрерывная линия) по теоретическому профилю относительных скоростей по толщинам пограничных слоёв при турбулентных течениях.

 

Напрямую численное решение уравнения (2) довольно неустойчиво. В качестве иллюстрации на рис. 3 показано сравнение приближённого решения (15) с прямым численным решением уравнения (2) при задании граничных условий в точке η=6.

 

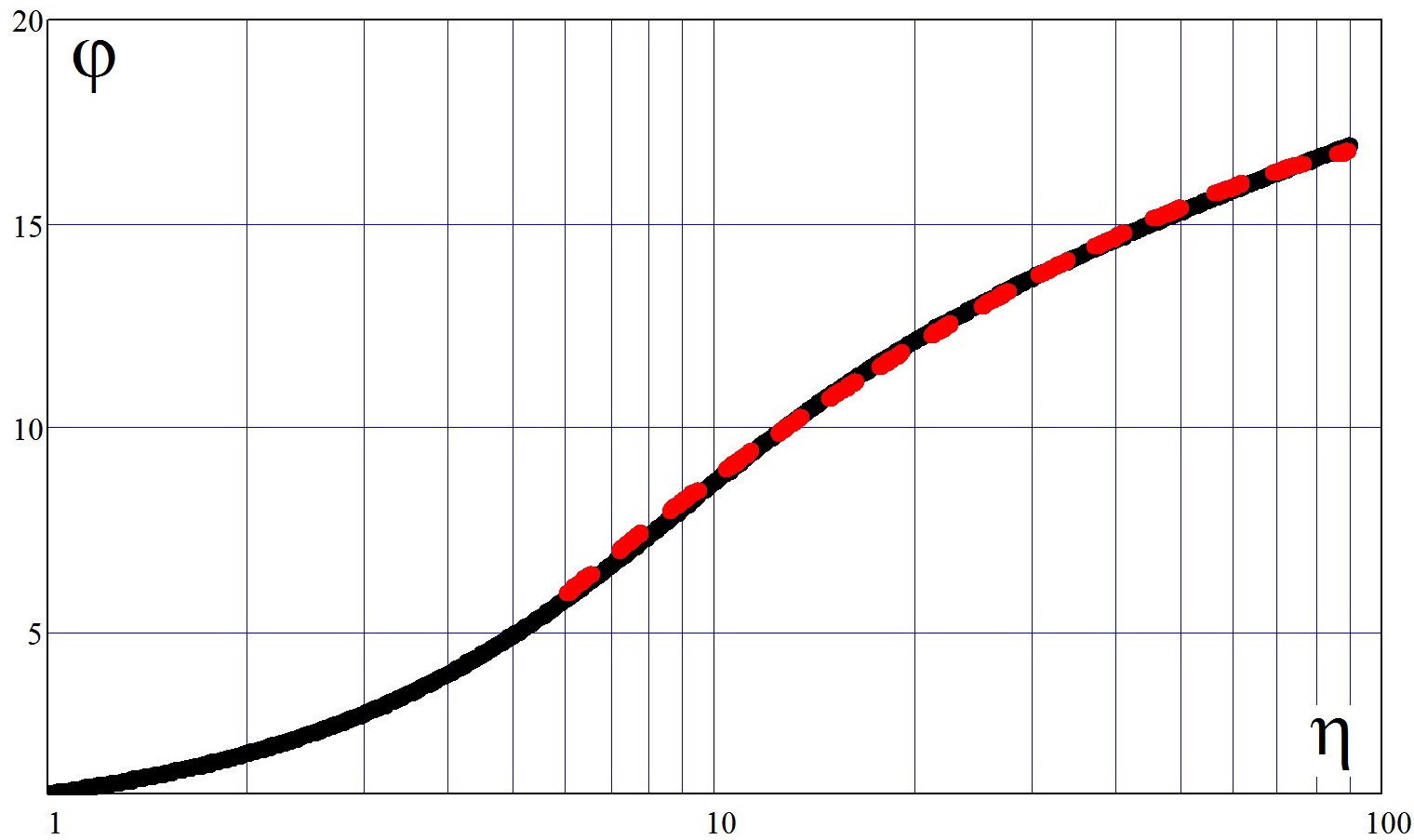
Рис. 3. Сравнение приближённого решения (15) (непрерывная линия) с непосредственными численными решениями дифференциального уравнения (2) (пунктирная линия) для задания граничных условий в точке с η=6.

 

Как видно из рис. 3, корреляция вышеуказанных решений очень хорошее, что указывает на адекватность предложенных решений способом последовательного приближения.

Cледовательно, полученные в данной статье приближённые решения, полученное при реализации способа последовательного приближения и с применением асимптотических функциональных граничных условий, можно применять на практике, поскольку они хорошо согласуются как с экспериментом, так и с прямым численным решением базового дифференциального уравнения.

ОСНОВНЫЕ ВЫВОДЫ

B cтатье было были получены приближённые аналитические интегрально-аппроксимационные решения, полученные при использовании асимптотических функциональных граничных условий с применением способа последовательного приближения, хорошо согласующееся и с прямым численным решением базового дифференциального уравнения, и с классическими экспериментальными данными.

1. Кутателадзе С.С. Основы теории теплообмена. — М.: Атомиздат, 1979. — 416 с.
2. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. — М.: Энергия, 1975. — 488 с.
3. Теория тепломассообмена / Под ред. А.И.Леонтьева. — М.: Изд-во МГТУ им. Н.Э.Баумана, 1997. — 683 с.
4. Лобанов И.Е. Решение задачи о теоретическом профиле безразмерной скорости по толщине пограничного слоя при турбулентном течении в пограничном слое на основе решения дифференциального уравнения Aбеля второго рода с применением функции Ламберта // Вестник научно-технического развития: Интернет-журнал. — 2018. — № 11 (135). — С. 29—38. — Peжим доступа: http://www.vntr.ru/vols/2018-02/3vntr02-126.pdf. — DOI: 10.18411/vntr2018-135-3.
5. Лобанов И.Е. Теоретическое детерминирование профиля безразмерной продольной скорости в турбулентном пограничном слое на основе решения обыкновенного дифференциального уравнения Абеля второго рода при использовании специальной функции Ламберта // Инновационные подходы в отраслях и сферах. — 2019. — Том № 4. — Bыпуск № 3 (март, 2019). — Режим доступа: http://inf16.ru/vypusk-3-mart-2019.
6. Ляхов В.К., Мигалин К.В. Эффект тепловой или диффузионной шероховатости. — Саратов: Издательство Саратовского университета, 1990. —176 с.
7. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции: Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. — М.: Наука, 1966. — 296 с.
8. Дубинов А.Е., Дубинова И.Д., Сайков С.К. W-функция Ламберта и её применение в математических задачах физики. — Саров: ФГУП "РФЯЦ–ВНИИЭФ", 2006. — 160 с.
9. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. — М.: Наука, 1965. — 577 с.

Комментарии пользователей:

Оставить комментарий