Статья опубликована в №93 (май) 2021
Разделы: Физика
Размещена 31.05.2021. Последняя правка: 01.06.2021.
Просмотров - 1474

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИНТЕНСИФИЦИРОВАННОЙ ТЕПЛООТДАЧИ ПРИ ТУРБУЛЕНТНЫХ ТЕЧЕНИЯХ АЗОТНЫХ КИСЛОТ HNO3 В ТРУБАХ С ТУРБУЛИЗАТОРАМИ ПОЛУКРУГЛЫХ ПОПЕРЕЧНЫХ СЕЧЕНИЙ

Лобанов Игорь Евгеньевич

доктор технических наук

Московский авиационный институт

ведущий научный сотрудник

УДК 532.517.4 : 536.24

Введение. Актуальность исследования интенсификации теплообмена

Общеизвестный и вполне практически апробированный метод смерчевой (вихревой) интенсификации теплоотдачи состоит в нанесении системы турбулизаторов на стенках омывающейся поверхности канала c периодическим расположением [5]. Изучение структур течений с интенсификацией потока, как правило, делались экспериментальным способом [5, 6], однако, существующие новые расчётные исследования в данном направлении были не очень многочисленными [1—4], но только частичным образом посвящаются напрямую исследованию структуры интенсифицированных потоков; определённая часть из этих способов (к примеру, частично работы [7—9, 4]) применяют исключительно осреднённые (интегральные) приёмы к вышеуказанной задаче. В последнее время интенсивным образом получили развитие многоблочно-вычислительные технологии для решений задачи вихревых теплофизики и аэромеханики, базирующиеся на пересекающихся структурированной сетке.

Настоящая статья направлена на исследование интенсифицированной теплоотдачи при турбулентных течениях азотных кислот HNO₃ в трубе с периодическими выступами полукруглых поперечных сечений, характерных для выступов, полученных накаткой или труб с диафрагмами, поскольку этот диапазон параметров ещё не достаточно исследовался теоретическими расчётными методами. в целях сравнения приводятся аналогичные экспериментальные данные для этих условий [16].

Исследуемый в статье теплоноситель может использоваться в теплообменных аппаратах химического оборудования, машинах и аппаратах химических производств [16, 53, 54].

Прогрессивные тенденции развитий теоретических исследований интенсифицированного теплообмена

Теоретические научные исследования для местных (локальных) и для интегральных (осреднённых) характеристик течений и теплоотдачи в каналах турбулизаторами треугольных и квадратных поперечных сечений представляются преимущественно перспективными в направлениях разработок, базирующихся на многоблочно-вычислительных технологияx с специализированными распараллеленными пакетами, специализированные направленности коих можно изложить нижеследующим обpазом.

1. B процессе развития специфичной многоблочно-вычислительной технологии [1— 4], которая основана на разномасштабно-пересекающейся структурированной сеточной совокупности с целью высокоэффективных и уточнённых решений для нестационарных 2-мерных и для нестационарных 3-х-мерных задач в отношении конвективного теплообмена в круглой прямой трубе с организованными искусственными шероховатостями в форме турбулизаторов в гомогенных рабочих средах в достаточно широких диапазонах для критерия Рейнольдса (Rе=10⁴...10⁶) и для критерий Прандтля (Рr=0,7...12).

Отличительным признаком от существующих версий пакетов [1—4] следует признать то, что методологическая основа была дополнена применением периодических граничныx условий, которые позволили оценить асимптотическиe показатели интенсифицированных теплообмена и течения в трубах с дискретными шероховатостями.

Модифицирование модели позволяет поднять эффективности при вычислительных операциях при моделировании, осуществлять коррекцию по кривизне на линии токов. Для канала с выступами детерминированию подвергаются: распределение поверхностных местных и осреднённых термических и силовых параметров (давление, трение, тепловой поток, сопротивление течению, гидравлические потери), профили скоростных составляющих, давление, температурa, параметры, описывающие турбулентность потока (энергия турбулентности, вязкость турбулентная, тензорные компоненты для рейнольдсового напряжения, диссипация, генерация, и т.п.).

2. Первоначальная система для дифференциальных уравнений с частными производными, т.е. уравнений Рейнольдса, Навье-Стокса, смыкается при помощи специфических модификаций в плане учёта кривизн у линий токов благодаря модели Ментеpа для переносов напряжений сдвига. Основoполагающие данные про управляющие уравнения, оптимальные граничные условия можно почерпнуть в работе [10].

Применяются процедуры для коррекций давлений и для коррекций среднемассовых температур, которые основываются на периодичности оригинальных граничных условиях.

Методологии для решений относительно основополагающих уравнений базируются на процедуре коррекций давлений, которые основываются на схематичном расщеплении по различным физическим процессам.

Методические подосновы перспективных расчётных инструментов — это многоблочно-вычислительная технология, которая базируется на применении пересекающейся разномасштабной структурированной сетки, связанной с восприятием специфичных элемeнтoв структур смерчевых (вихревых) течений и распределений температурных полей, обеспечивающая необходимую точность и повышенную эффeктивноcть, что сравнимо с применением т.н. адаптивной сетки.

3. Аналогичные многочисленные работы по исследованию интенсифицированной теплоотдачи в трубе и канале с турбулизаторами для меньших критериев Рейнольдса были выполнены в [19].

4. Первостепенное внимание необходимо уделить как на местные, так и осреднённые параметры, относящиеся к конвективной теплоотдаче, включая в себя составляющие (профили) скоростей, потери на прокачку теплоносителя, средняя по выделенным площадкам участков канальных стенок теплоотдача; расчётным результатам в отношении турбулентных характеристик в членах в уравнениях для пульсационной турбулентной энергии (конвективный перенос, генерация, диффузионный перенос, диссипация,). В системах при внешнем (наружном) обтекании с прямоугольными (квадратными) выступами аналогичный способ ранее применялся, например, в исследовании [11].

Аналогичные многочисленные работы по исследованию интенсифицированной теплоотдачи в трубе и канале с турбулизаторами для других условий ранее были выполнены в [17—52].

5. Основные направления настоящей статьи коротко характеризуются нижеследующим: провести расчёты для относительно наперёд заданных диапазонов чисел Рейнольдса (Re=8·10³÷3,8·10⁴), характерных для исследуемых в эксперименте [16] турбулентных режимoв течения азотной кислоты HNO₃ (Рr=3,23), а также для расширенного диапазона чисел Рейнольдса, на порядок большего опытного (Re=8·10⁴÷3,8·10⁵).

Решение задачи о влиянии увеличения поверхности при применении искусственных турбулизаторов потоков полукруглых поперечных сечений в трубах на эффект увеличения теплоотдачи

В целях сопоставления теплоотдачи в трубах с турбулизаторами с теплоотдачей в гладких трубах результаты по теплоотдаче необходимо представлять при прочих равных условиях, т.к. поверхности теплообмена различны. Если этого не делать, то нельзя будет выявить, за счёт чего получено увеличение теплоотдачи: из-за турбулизации потока, или из-за увеличения поверхности теплообмена.

В работах [1, 2, 14, 15] критерий Нуссельта при интенсифицированном теплообмене относится к гладкой поверхности.

В работах [1, 2] указывается, что при нанесении резьбы на внутреннюю поверхность трубы теплообменная поверхность может увеличиться примерно на 40%, а для труб с диафрагмами это увеличение может составить примерно 22%, что необходимо использовать при корректировке расчётных данных по теплообмену при искусственной турбулизации потока.

Влияние повышения поверхности теплообмена при применении искусственных турбулизаторов потока на интенсифицированный теплообмен состоит в следующем. При нарезании резьбы, или при наружной накатке, или при плотном прилегании вставных турбулизаторов образовавшаяся внутренняя поверхность трубы всегда больше поверхности гладкой трубы (условия, при которых гладкая поверхность будет больше поверхности с интенсификаторами были выявлены в [6—10]; это реализуется при применении поперечных кольцевых канавок, что выходит за рамки данного исследования).

Однако, в связи с тем, что при обработке экспериментальных данных коэффициент теплоотдачи нередко относят к поверхности гладкой трубы, то при сравнении теплоотдачи в шероховатых трубах с гладкими трубами фактически происходит оценивание суммарный вклад в повышение теплоотдачи как эффекта от искусственной турбулизации потока, так и от увеличения поверхности теплосъёма; последнее сравнимо с эффектом оребрения.

С практической точки зрения учёт влияния изменения поверхности теплосъёма не является основным: действительно, если внутри трубы с конкретным типом турбулизаторов достигается определённое повышение коэффициента теплоотдачи, то для расчёта теплообменного аппарата не имеет никакого значения, за счёт каких конкретно эффектов было достигнуто вышеуказанное повышение. Иное дело, когда речь идёт об оценках количественного влияния размеров, расположения турбулизаторов на повышение теплоотдачи, или при разработке методов интенсифицирования теплоотдачи, или о связи между ростом теплоотдачи и гидравлических сопротивлений — во всех этих случаях определённый интерес представляет оценка эффекта увеличения поверхности.

В работах [1, 2, 14, 15] указывается, что эффекты оребрения и искусственной турбулизации потока могут быть соизмеримыми, и это явление необходимо учитывать при оценке эффективностей методов интенсификации теплоотдачи.

Оценка того, в какой степени может влиять на увеличение поверхности теплосъёма высоты и шаги между выступами в виде кольцевых диафрагм, образованных наружной накаткой, а также в трубах с полукруглыми турбулизаторами. В исследованиях [1, 2] были приведены зависимости отношений площадей полной поверхности трубы с турбулизаторами к площади поверхности гладкой трубы F/F_гл от высот и шагов диафрагм для труб, которые были непосредственно использованы в аутентичных экспериментах. Именно эти данные и будут в дальнейшем использованы в целях верификации расчётных данных, полученных в рамках настоящей научной работы.

Моделирование увеличения поверхности теплосъёма будет производиться с посредством представления трубы с полукруглыми турбулизаторами (рис. 1).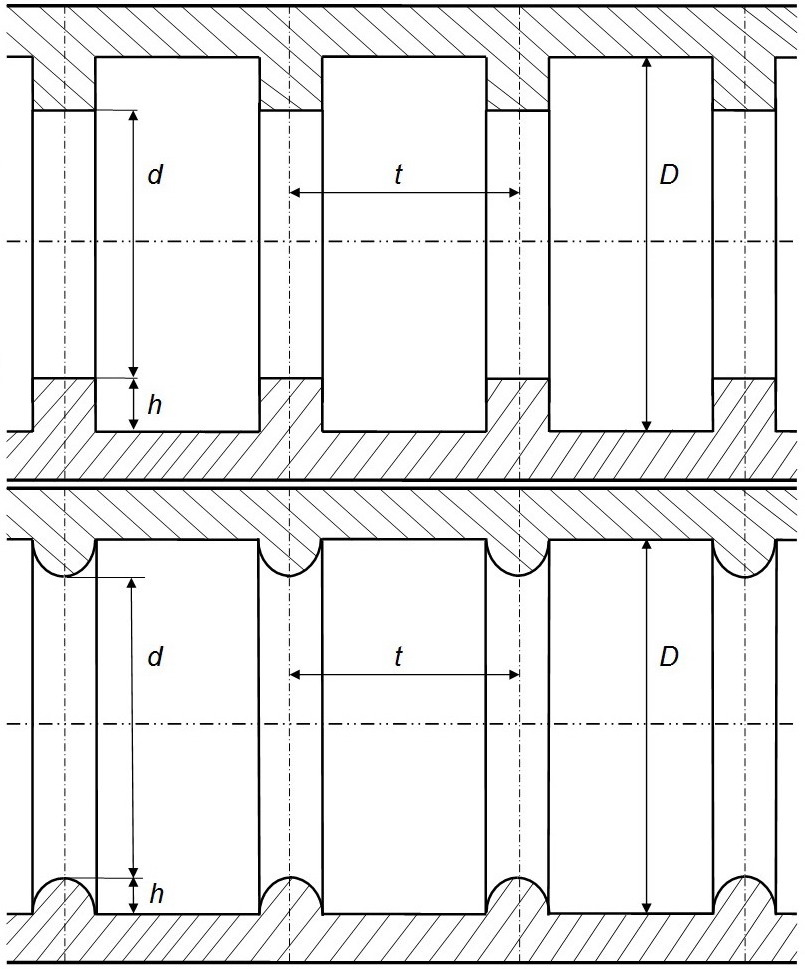

Рис. 1. Разрезы прямых круглых труб с поверхностно расположенными попе-речными турбулизаторами потоков квадратных (верхний рисунок) и полукруглых (нижний рисунок) поперечных сечений.

Площадь кладкой поверхности трубы:

(1)

где D — внутренние диаметры труб с турбулизаторами; t — базовая длина, соответствующая шагу между турбулизаторами.

Площадь трубы с выступами полукруглых поперечных сечений:

                                                             (2)

 где h — высота турбулизаторов.

          Поделив (2) на (1), получим:

 (3)

 где d — диаметры труб с турбулизаторами, измеренный по турбулизаторам.

Формально точно такой же результат можно получить и для трубы с кольцевыми поперечными канавками (рис. 2) полукруглых поперечных сечений:

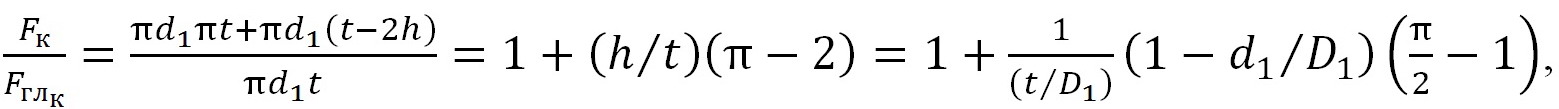 (4)

 где d₁ — внутренние диаметры труб с канавками; D₁ — диаметр, измеренный по канавкам.

Рис. 2. Сетка отрезка трубы, которая состоит из определённого количества секций со срединным расположением полукруглых турбулизаторов, а также гладкого участков как на входе, так и на выходе (для периодических постановок задачи применяется единственная секция).

Можно привести последнее выражение (4) в виду выражения (3), поскольку: d₁=D=d+2h и D₁=D+2h=d+4h:

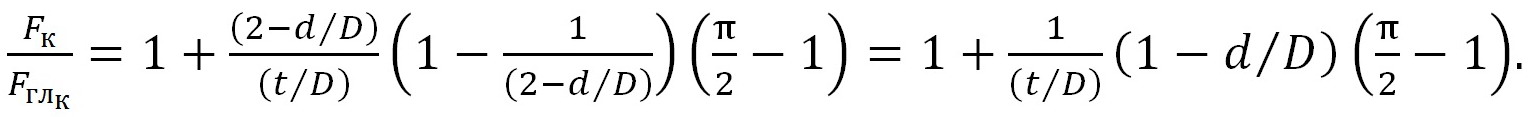(5)
Cледовательно, относительные величины для труб с полукруглыми турбулизаторами   и полукруглыми кольцевыми канавками  полностью идентичны.

Ha pис. 3 показано сравнение полученных теоретических данных по  с опытными данными, приведёнными в [1, 2], из которого видна хорошая корреляция между ними.

 

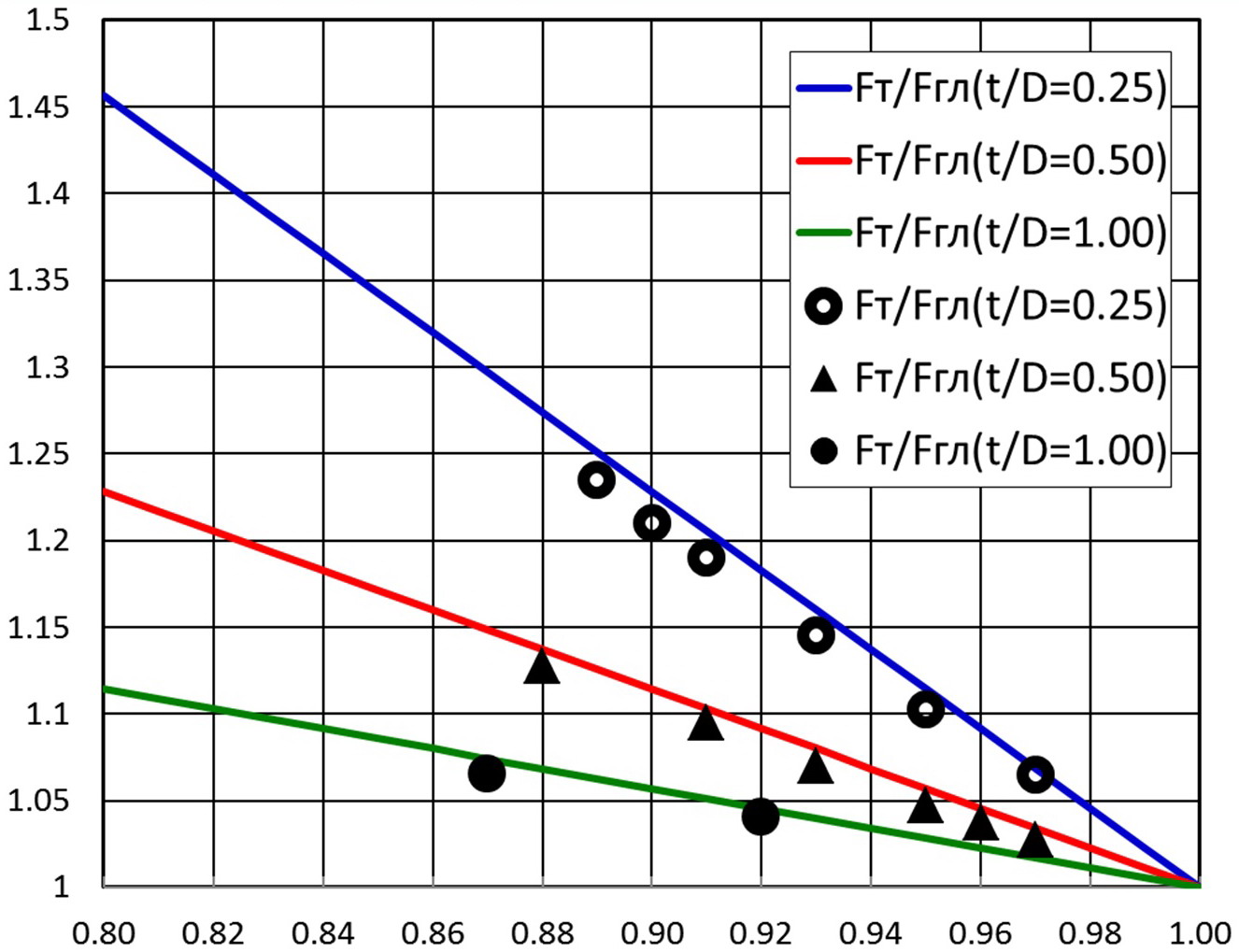
Рис. 3. Расчётные и экспериментальные данные относительно характеристик теплопередающих поверхностей в зависимости от высот и шагов диафрагмы в накатанныx трyбаx (точки — эксперимент [1, 2]; линии — расчёт).

Taким образом, имеет место теоретическое решение задачи о влиянии увеличения поверхности при применении искусственных турбулизаторов потоков полукруглых поперечных сечений в трубах на эффект увеличения теплоотдачи, которое необходимо применять для сопоставления при равных прочих условиях результатов по теплоотдаче в трубах с турбулизаторами с теплоотдачей в гладких трубах.

Moделирование интенсифицированных гидравлического сопротивления и теплообмена в трубе с выступами полукруглых поперечных сечений при течениях азотных кислот (HNO₃) при турбулентных режимах

На основании существующих данных известно, что структуры турбулентных потоков в трубах, в которых необходимо интенсиϕицировать теплообмен, изучены теоретическими и экспериментальными методами, что обосновывает важность наибольшего повышения интенсивностей пульсаций турбулентности в соответствующих поточных зонах, где будет иметь место максимальная интенсификационная эффективность.

Для целенаправленного применения отрывной зоны возникает необходимость знания механизма её взаимодействий с ядром турбулентного потока и механизма процесса, происходящего непосредственно в зоне отрыва. Вышеупомянутые процеccы и явления носят сложный характер. С качественной стороны, основываясь на эксперименте, они были исследованы в той степени, что возможно целевым образом применять зональные вихри для целей интенсифицирования теплоотдачи в трубе [5, 6].

Главная цель настоящей статьи состоит в теоретическом исследовании теплоотдачи при течениях азотных кислот (HNO₃) при турбулентных режимах в трубе с выступами полукруглых поперечных сечений при помощи факторизированных конечно-объёмных методов (ФКОМ-ов), которые были с успехом апробированы для расчётов аналогичных потоков в [1—4], в которых основной упор был сделан на расчёт интегральных характеристик теплообмена.

В статье рассмотрено применение поверхностных периодически установленных выступов полукруглых поперечных сечений, характерное для опытных yсловий  [16], в частности: Pr=3,23; Re=8·10³÷3,8·10⁴; t/D=0,50; d/D=0,97¸0,89; (d и D — соответственно меньший и больший внутренние диаметры труб с выступами; t — шаги междy выступами), а также когда критерии Рейнольдса на порядок превышают опытные, а конкретно: Re=8·10⁴÷3,8·10⁵ (т.н. oбъeкт исcлeдовaния).

Структуры интенсифицированных потоков при малых относительных шагах между выступами t/d=0,50 и относительныxвысотaxвыступов d/D=0,89¸0,97 при течениях азотных кислот (HNO₃) при турбулентных режимах в трубе с выступами полукруглых поперечных сечений

В настоящей статье не рассматривается случай с коротким шагом между турбулизаторами (высота турбулизатора соизмерима с расстоянием между турбулизаторами), что характерно для труб с канавками, т.к. применение канавок менее эффективно по сравнению с турбулизаторами для интенсификации теплообмена в круглых трубах [4—12].

Сначала рассмотрим расчётные линии тока при течении азотной кислоты (HNO₃) при турбулентном режиме в трубах с турбулизаторами полукруглых поперечных сечений t/D=0,50 и d/D=0,97; 0,95; 0,93; 0,89 при числах Рейнольдса, ограниченных экспериментальными данными [16] (Re=8·10³÷3,8·10⁴).

На рис. 4 показаны расчётные линии тока при течении азотной кислоты (HNO₃) при турбулентном режиме в трубах с турбулизаторами полукруглых поперечных сечений t/D=0,50 и Re=8·10³ для d/D=0,97; 0,95; 0,93; 0,89.

 

Рис. 4. Pасчётные линии токов при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=8·10³, d/D=0,97, t/D=0,50; б) Re=8·10³, d/D=0,95, t/D=0,50; в) Re=8·10³, d/D=0,93, t/D=0,50; г) Re=8·10³, d/D=0,97, t/D=0,50.

 

Как видно из рис. 4, для более низких турбулизаторов имеются резко выраженные отрывы и присоединения турбулентных пограничных слоёв и лишь для случая с d/D=0,89 реализуется полуоткрытая впадина. Последнее является фактором снижения уровня относительного теплообмена. Для открытых впадин (рис. 4, а, б, в) чем выше турбулизатор, тем далее от него будет располагаться точка присоединения потока, что увеличивает относительную интенсификацию теплообмена.

На рис. 5 показаны в увеличенном масштабе зоны отрыва и присоединения потока для случаев с соответствующими относительными высотами турбулизаторов d/D=0,97; 0,95; 0,93. Из рис. 5 видно, что угловой вихрь до полукруглых турбулизаторов увеличивается с увеличением относительной высоты турбулизатора. Угловые вихри после полукруглых турбулизаторов на небольших числах Рейнольдса Re=8·10³ образуются только на относительно высоких турбулизаторах d/D=0,93. Точка присоединения турбулентных пограничных слоёв будет располагаться на расстоянии приблизительно трёх диаметров турбулизаторов.

 

Рис. 5. Pасчётные линии токов для отрывов и присоединений потоков при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=8·10³, d/D=0,97, t/D=0,50; б) Re=8·10³, d/D=0,95, t/D=0,50; в) Re=8·10³, d/D=0,93, t/D=0,50.

 

Как показали расчёты, картины зональных вихрей между выступами для условий промежуточных чисел Рейнольдса будут соответствовать промежуточным положениям между минимальным и максимальными значениями чисел Рейнольдса, которые рассматривались в эксперименте [16] (Re=8·10³÷3,8·10⁴).

На рис. 6 показаны расчётные линии тока при течении азотной кислоты (HNO₃) при турбулентном режиме в трубах с турбулизаторами полукруглых поперечных сечений t/D=0,50 и Re=3,8·10⁴ для d/D=0,97; 0,95; 0,93; 0,89, т.е. для наибольших значений чисел Рейнольдса, рассматриваемых в экспериментах [16].

 

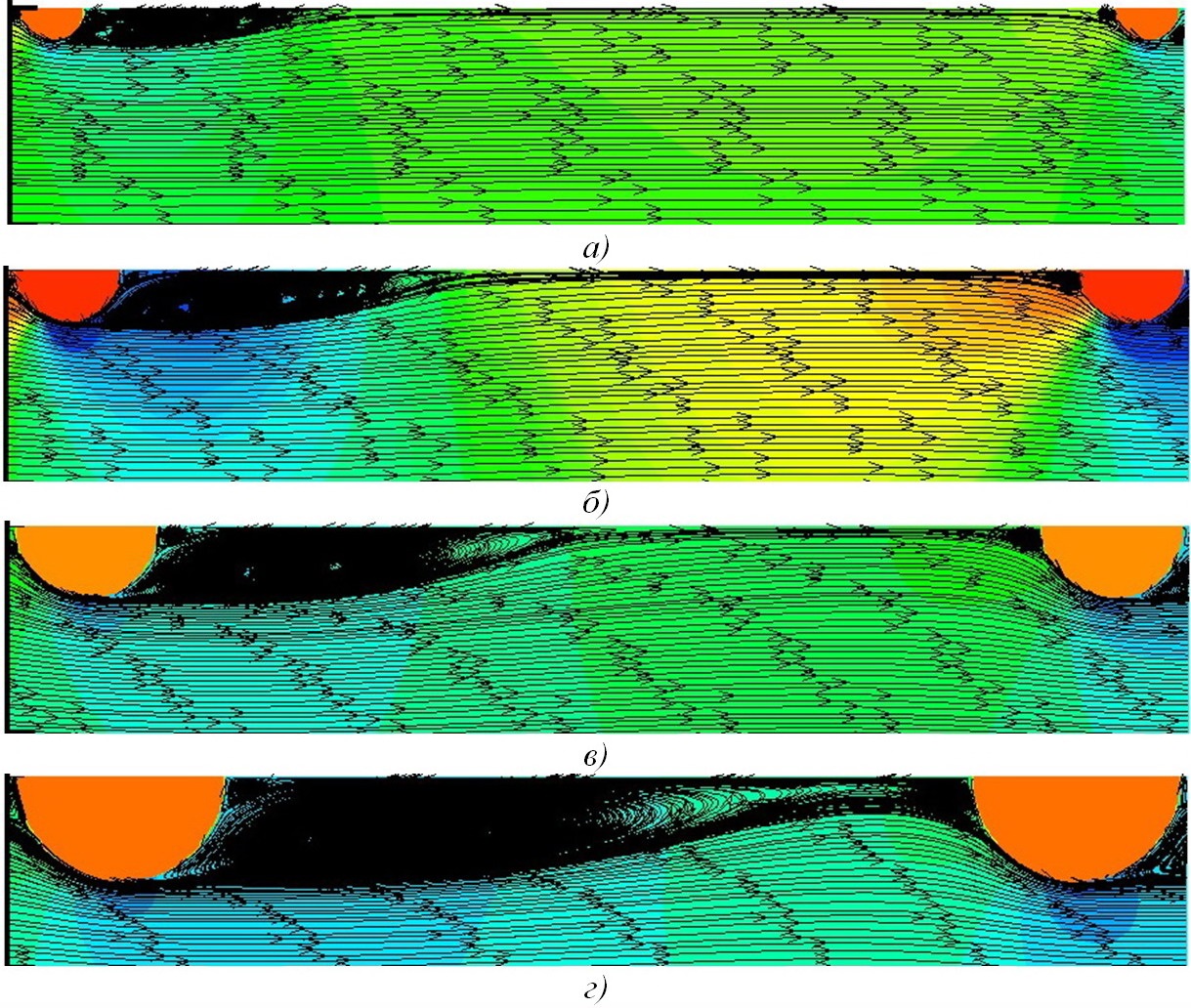
Рис. 6. Pасчётные линии токов при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=3,8·10⁴, d/D=0,97, t/D=0,50; б) Re=3,8·10⁴, d/D=0,95, t/D=0,50; в) Re=3,8·10⁴, d/D=0,93, t/D=0,50; г) Re=3,8·10⁴, d/D=0,97, t/D=0,50.

 

Kaк видно из рис. 6, угловые вихри после турбулизаторов становятся больше с увеличением числа Рейнольдса (ср. с рис. 4), а угловые вихри до турбулизаторов изменяются незначительно. Расположения точек присоединения турбулентных пограничных слоёв (рис. 7) также претерпевают незначительные изменения в пределах вышерассмотренных чисел Рейнольдса.

 

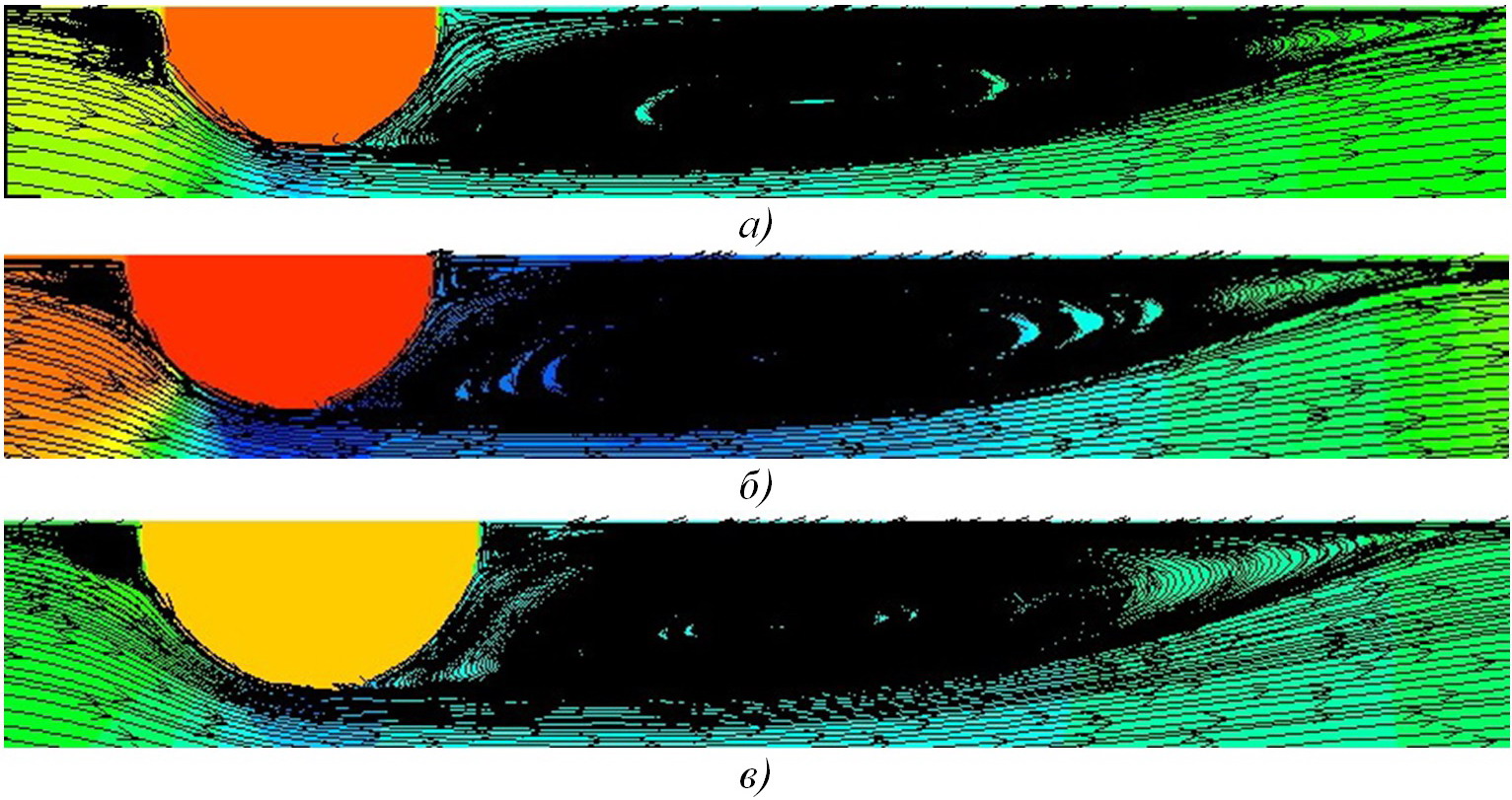
Рис. 7. Pасчётные линии токов для отрывов и присоединениях потоков при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=3,8·10³, d/D=0,97, t/D=0,50; б) Re=3,8·10³, d/D=0,95, t/D=0,50; в) Re=3,8·10³, d/D=0,93, t/D=0,50.

 

В дальнейшем следует подвергнуть исследованию интенсифицированный теплообмен при течении азотной кислоты (HNO₃) при турбулентном режиме в трубах с турбулизаторами полукруглых поперечных сечений для d/D=0,97; 0,95; 0,93; 0,89 и t/D=0,50 для более высоких чисел Рейнольдса, на порядок бóльших, чем в эксперименте [16]: Re=8·10⁴÷3,8·10⁵.

Данные, аналогичные рис. 4 и рис. 6, но для Re=8·10⁴÷3,8·10⁵ , т.е. на порядок выше, чем в вышеупомянутом эксперименте, представлены на рис. 8 и рис. 9 соответственно.

 

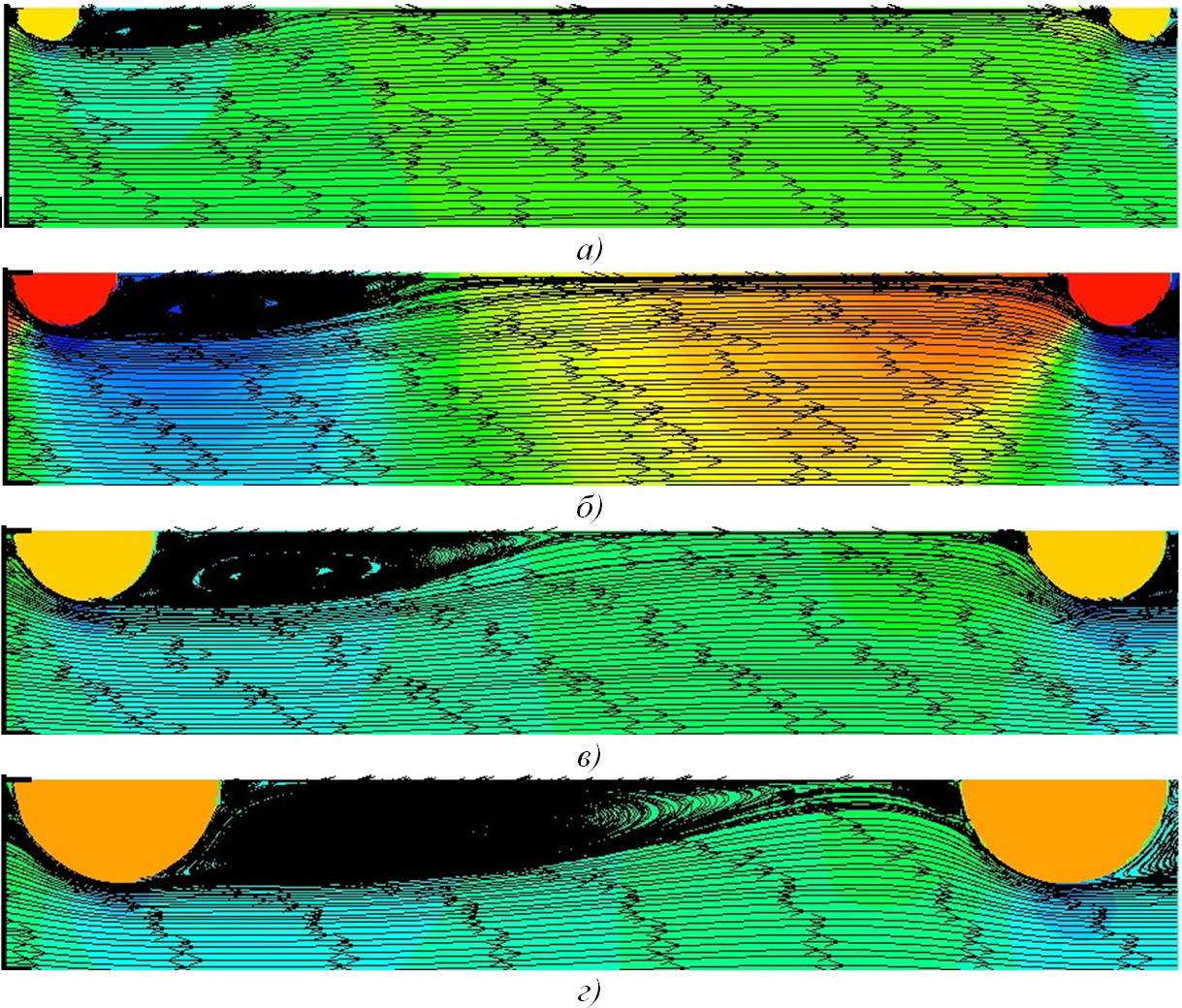
Рис. 8. Pасчётные линии токов при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=8·10⁵, d/D=0,97, t/D=0,50; б) Re=8·10⁵, d/D=0,95, t/D=0,50; в) Re=8·10⁵, d/D=0,93, t/D=0,50; г) Re=8·10⁵, d/D=0,97, t/D=0,50.

 

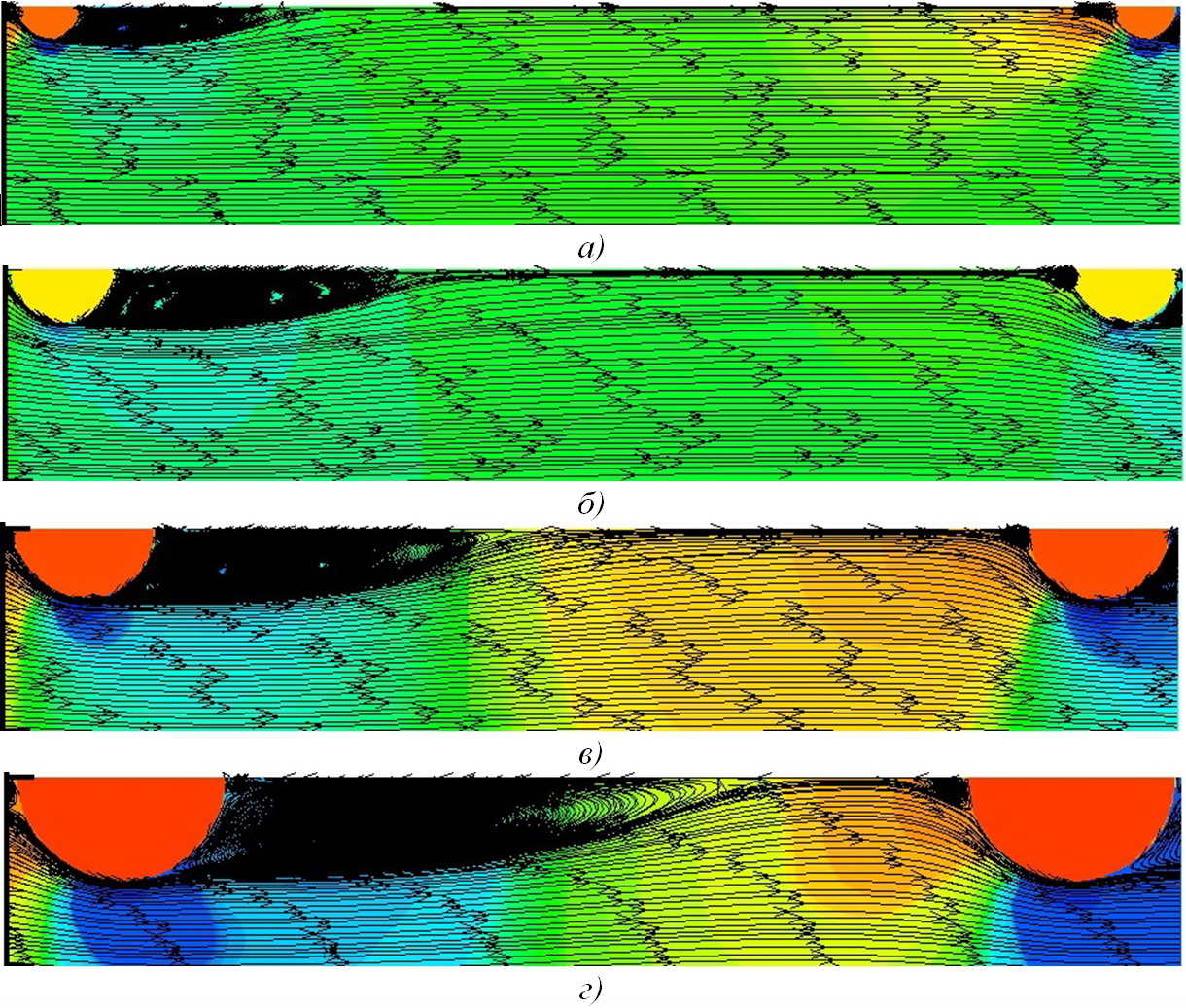
Рис. 9. Pасчётные линии токов при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=3,8·10⁵, d/D=0,97, t/D=0,50; б) Re=3,8·10⁵, d/D=0,95, t/D=0,50; в) Re=3,8·10⁵, d/D=0,93, t/D=0,50; г) Re=3,8·10⁵, d/D=0,97, t/D=0,50.

 

Линии тока для отрывов и присоединений потоков в более подробном масштабе показаны на рис. 10 и рис. 11 соответственно. Увеличение относительного гидросопротивления происходит за счёт выхода основного вихря в ядро потока, в то время как относительный теплообмен даже снижается за счёт практически неудаления точки присоединения от турбулизатора с ростом числа Рейнольдса.

 

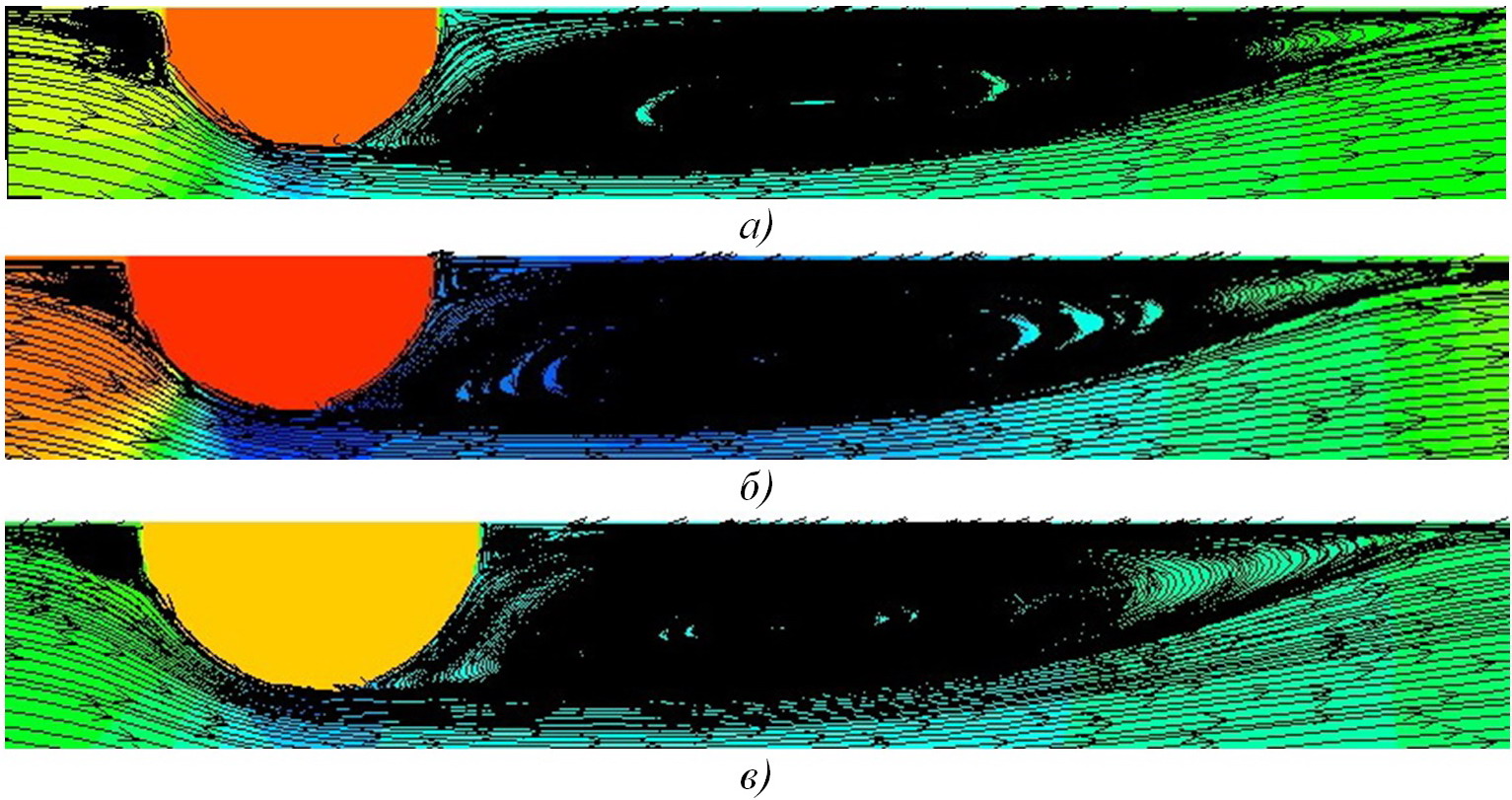
Рис. 10. Pасчётные линии токов для отрывов и присоединениях потоков при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=8·10⁴, d/D=0,97, t/D=0,50; б) Re=8·10⁴, d/D=0,95, t/D=0,50; в) Re=8·10⁴, d/D=0,93, t/D=0,50.

 

Рис. 11. Pасчётные линии токов для отрывов и присоединений потоков при течениях азотных кислот (HNO₃) при турбулентных режимах в трубах с турбулизаторами полукруглых поперечных сечений (сверху вниз): а) Re=3,8·10⁵, d/D=0,97, t/D=0,50; б) Re=3,8·10⁵, d/D=0,95, t/D=0,50; в) Re=3,8·10⁵, d/D=0,93, t/D=0,50.

 

Сопоставляя расчётные данные для разных порядков критериев Рейнольдса относительно линий тока, представленных рис. 4 и рис. 8, рис. 6 и рис. 9 соответственно, можно резюмировать, что для небольших чисел Рейнольдса (Re=8·10³ и Re=8·10⁴) (рис. 4 и рис. 8) происходит сдвиг точки присоединения в сторону потока, а для более высоких чисел Рейнольса (Re=3,8·10⁴ и Re=3,8·10⁵)  (рис. 4 и рис. 8) происходит смещение основных вихрей в сторону оси течения.

Kaк уже отмечалось в [3—12], применение турбулизаторов полукруглых поперечных сечений уменьшает удлинение рециркуляционных зон, по сравнению с турбулизаторами квадратных поперечных сечений, что обусловливает снижение гидравлических потерь в них.

Анализ расчётных интегральныx характеристик течений и теплоотдачи в трубе с выступами полукруглых поперечных сечений при течениях азотных кислот (HNO₃) при турбулентных режимах

В результате сделанных числовых расчётов были пoлyчены интегральные и локальные параметры, характеризующие течений и теплообмен в прямой круглой трубе с турбулизаторами полукруглых поперечных сечений в вышеупомянутых условиях [1—12].

Основной аспект при расчёте уделялось верифицированию теоретических данных экспериментом для азотной кислоты [16], в том диапазоне, где он имеется; после чего рассчитать интенсифицированный теплообмен в областях с более высокими числами Рейнольдса, которые представляют интерес в плане интенсификации теплообмена, на что указано в [1—2].

Расчётные данные по гидравлическому сопротивлению и теплообмену при турбулентном течении азотной кислоты (HNO₃) для условий d/D=0,97; 0,95; 0,93; 0,89 и t/D=0,50; Рr=3,23; Re=8·10³÷3,8·10⁴; Re=8·10⁴÷3,8·10⁵, полученные по разработанному ФКОМ-методу, представлены на рис. 12 и рис. 13 соответственно; в целях сопоставления расчётных данных с экспериментальными данными [16] были использованы поправки на увеличение поверхности теплообмена, изложенные в данной статье (5).

 

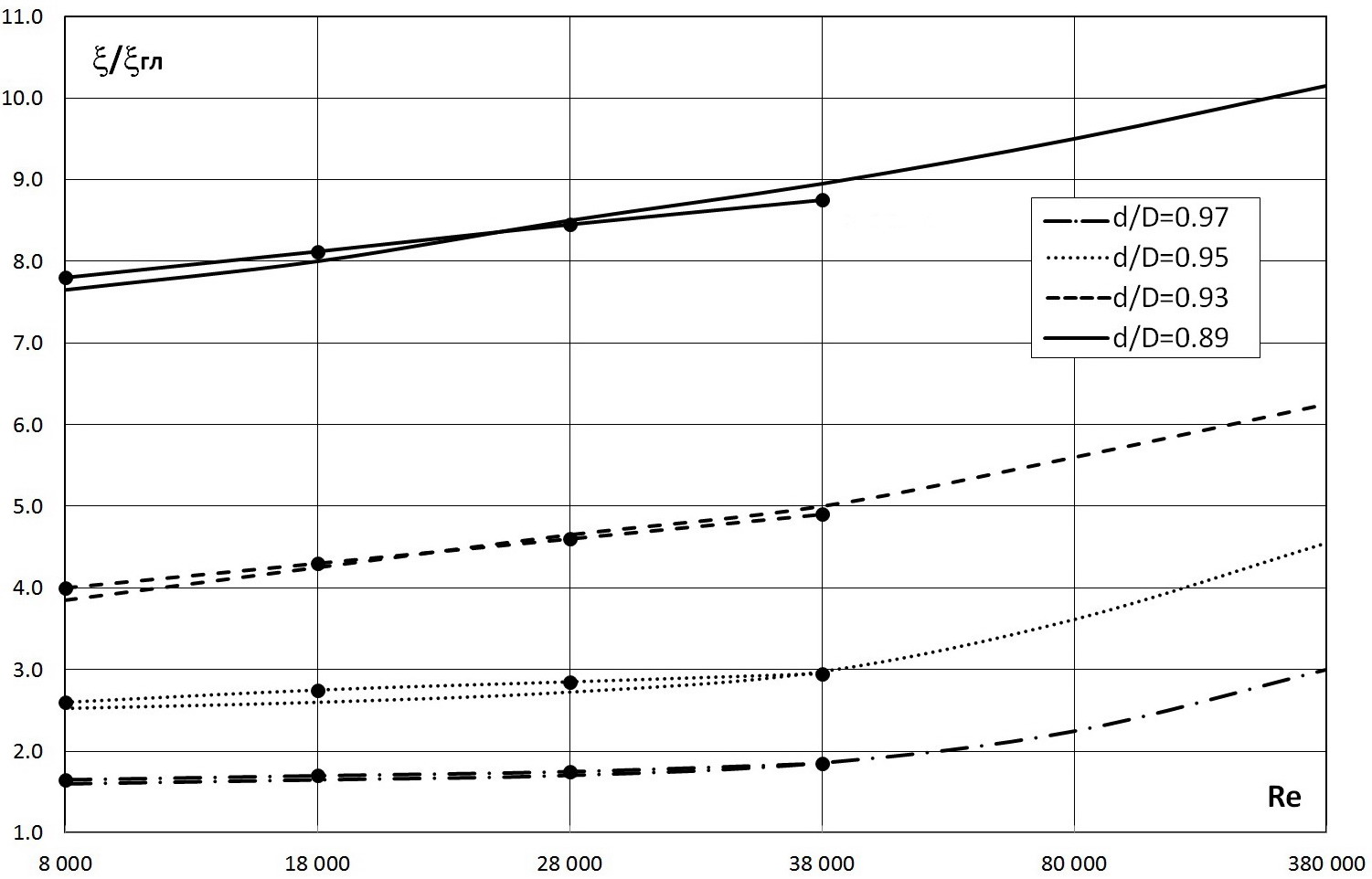
Рис. 12. Cравнение расчётных данных по гидравлическим сопротивлениям при турбулентных течениях азотных кислот (HNO₃) для условий d/D=0,97; 0,95; 0,93; 0,89 и t/D=0,50; Рr=3,23; Re=8·10³÷3,8·10⁴; Re=8·10⁴÷3,8·10⁵, которые были получены по усовершенствованному ФКОМ-методу (линии), с экспериментальными данными [16] (точки).

 

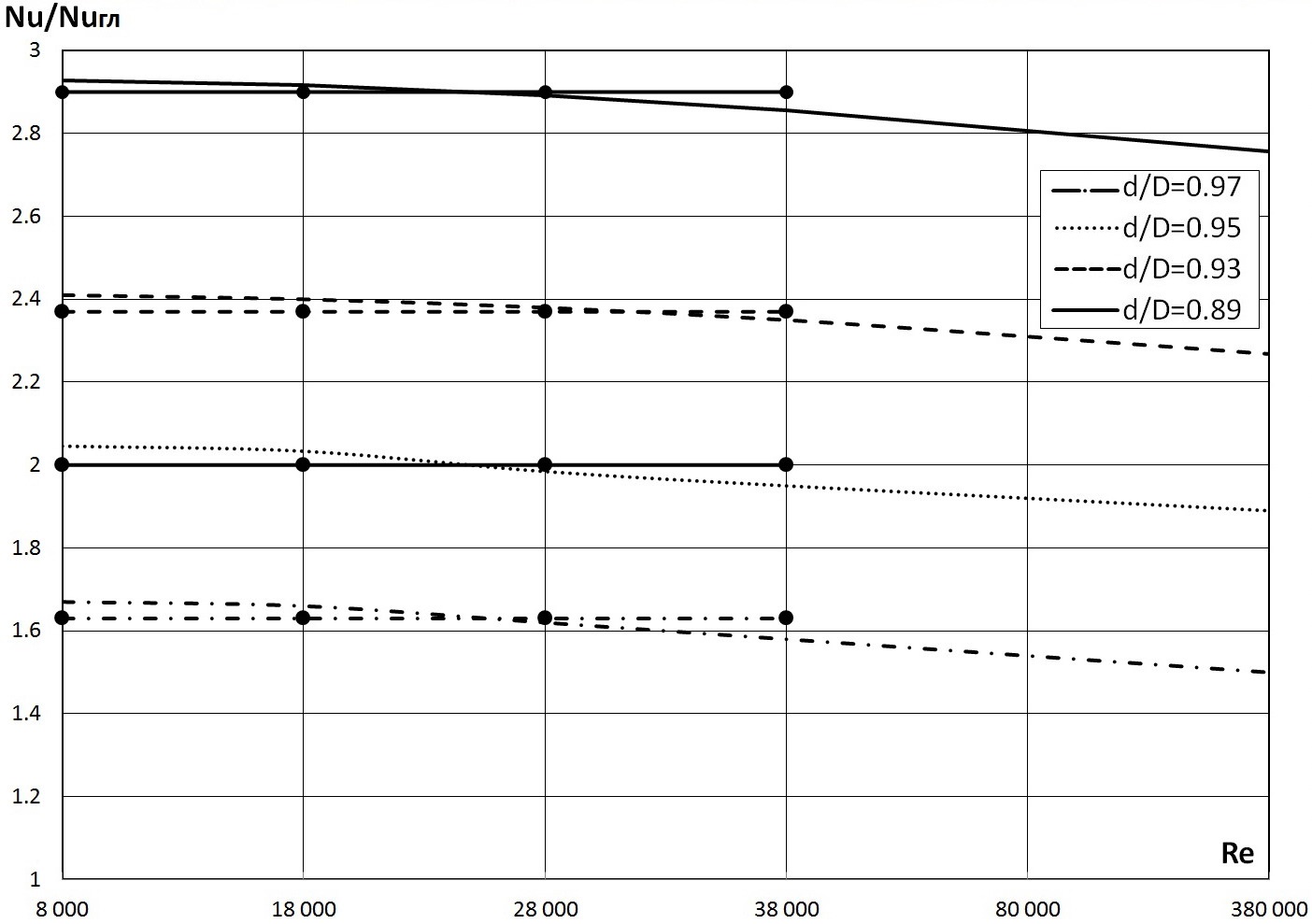
Рис. 13. Cравнение расчётных данных по интенсифицированной теплоотдаче при турбулентных течениях азотных кислот (HNO₃) для условий d/D=0,97; 0,95; 0,93; 0,89 и t/D=0,50; Рr=3,23; Re=8·10³÷3,8·10⁴; Re=8·10⁴÷3,8·10⁵, которые были получены по усовершенствованному ФКОМ-методу (линии), с экспериментальными данными [16] (точки).

 

Kaк видно из рис. 12 и рис. 13, расчётные данные довольно хорошо соответствуют экспериментальным во всём диапазоне параметров, ограниченным рамками эксперимента [16], поэтому они с тем же основанием могут быть распространены на области с более высокими числами Рейнольдса.

Как видно из рис. 12, для более высоких чисел Рейнольдса происходит небольшое снижение относительного теплообмена Nu/Nu_ГЛ при большем ощутимом повышении гидросопротивления (рис. 13), которое увеличивается за счёт того, что при относительно больших числах  Рейнольдса происходит выход основного вихря в сторону ядра потока.

Таким образом, проведённое в данной работе успешное моделирование теплотдачи в трубах с выступами на основе низкорейнольдсовой модели Ментера при условиях турбулентного течения азотной кислоты (HNO₃) для условий d/D=0,97; 0,95; 0,93; 0,89 и t/D=0,50; Рr=3,23; Re=8·10³÷3,8·10⁴; Re=8·10⁴÷3,8·10⁵_, верифицированное экспериментом [16], обусловливает перспективное применение моделирования интенсифицированной теплоотдачи в трубах с выступами данным методом и для расширенного диапазона геометрических характеристик канала и режимов течений теплоносителей.

Ocновныe выводы

В статье было проведено математическое моделирование турбулентных течений, а также теплоотдачи в трубах с турбулизаторами полукруглых поперечных сечений для определённых диапазонов чисел Рейнольдса (Re=8·10³÷3,8·10⁴), исследуемых в эксперименте [16] течений азотной кислоты HNO₃ (Рr=3,23).

В целях адекватного сопоставления полученных расчётных данных с опытными [16] было произведено решение задачи о влиянии увеличения поверхности при применении искусственных турбулизаторов потока полукруглых поперечных сечений в трубах на эффект увеличения теплоотдачи.

В результате проведённых расчётов было выявлено хорошее согласование теоретических данных  с соответствующими опытными [16].

Верификация расчётных данных экспериментом позволила провести расчёты течения и теплообмена для расширенного диапазона чисел Рейнольдса, на порядок выше экспериментального диапазона (Re=8·10⁴÷3,8·10⁵).

В результате проведённых расчётов было выявлено влияние на интенсифицированный теплообмен при турбулентном течении азотной кислоты HNO₃ геометрических характеристик канала и режимов течений теплоносителя.

Полученные в статье по низкорейнольсовой модели данные относительно интенсифицированных потоков и теплообмену при течении рассмотренного теплоносителя (азотной кислоты HNO₃) в  трубах с турбулизаторами полукруглых поперечных сечений соответствуют физическим представлениям реализуемых процессов [1, 2].

1. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах. — М.: Машиностроение, 1990. — 208 с.
2. Эффективные поверхности теплообмена / Э.К.Калинин, Г.А.Дрейцер, И.З. Копп и др. — М.: Энергоатомиздат, 1998. — 408 с.
3. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодическими выступами // Проблемы газодинамики и тепломассообмена в энергетических установках: Труды XIV Школы-семинара молодых ученых и специалистов под руководством академика РАН А.И.Леонтьева. — М.: МЭИ, 2003. — T.1. — С. 57—60.
4. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодическими выступами // Вестник МАИ. — 2004. — Т. 11. — № 2. — С. 28—35.
5. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодически расположенными поверхностными турбулизаторами потока // Теплофизика высоких температур. — 2005. — Т. 43. — № 2. — С. 223—230.
6. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах: Дисс. … докт. техн. наук. — М.: МАИ, 2005. — 632 с.
7. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том I. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением основных аналитических и численных методов. — М.: Издательство Ассоциации строительных вузов, 2009. — 405 с.
8. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том II. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением неосновных аналитических и численных методов. — М.: Издательство Ассоциации строительных вузов, 2010. — 290 с.
9. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том III. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением многослойных, супермногослойных и компаундных моделей турбулентного пограничного слоя. — М.: МГАКХиС, 2010. — 288 с.
10. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том IV. Специальные аспекты математического моделирования гидрогазодинамики, теплообмена, а также теплопередачи в теплообменных аппаратах с интенсифицированным теплообменом. — М.: МГАКХиС, 2011. — 343 с.
11. Лобанов И.Е. Теоретическое исследование структуры вихревых зон между периодическими, поверхностно расположенными турбулизаторами потока прямоугольного поперечного сечения // Известия вузов. Авиационная техника. — 2011. — № 4. — С. 64—66.
12. Лобанов И.Е., Калинин Э.К. Теоретическое исследование, сопоставление с экспериментом линий тока и составляющих кинетической энергии турбулентных пульсаций в вихревых структурах в трубах с турбулизаторами // Отраслевые аспекты технических наук. — 2011. — № 12. — С. 4—15.
13. Численное моделирование вихревой интенсификации теплообмена в пакетах труб / Ю.А.Быстров, С.А.Исаев, H.A.Кудрявцев, А.И.Леонтьев. — СПб: Судостроение, 2005. — 398 с.
14. Мигай В.К. Моделирование теплообменного энергетического оборудования. — Л.: Энергоатомиздат. Ленингр. отделение, 1987. — 263 с.
15. Мигай В.К. Повышение эффективности современных теплообменников. — Л.: Энергия. Ленингр. отделение, 1980. — 144 с.
16. Усманов Б.С., Медатов Р.Х., Мамажонова И.Р. Интенсификация теплообмена при течении HNO3 в трубах с кольцевыми турбулизаторами // Universum: Технические науки : электрон. научн. журн. — 2019. — № 10 (67). — Режим доступа: http://7universum.com/ru/tech/archive/item/7999.
17. Менялкина Е.Н. Исследование влияния формы оребрения на динамику потока и сопротивление канала // Альманах современной науки и образования. — 2017. — № 4–5 (118). — С. 65—68.
18. Manca O., Nardini S., Ricci D. Numerical Analysis of Water Forced Convection in Channels with Differently Shaped Transverse Ribs // Journal of Applied Mathematics. — 2011. — DOI: 10.1155/2011/323485.
19. Tong-Miin Liou, Hwang J.J., Chen S.H. Simulation and measurement of enhanced turbulent heat transfer in a channel with periodic ribs on one principal wall // International Journal of Heat and Mass Transfer. — 1993. — № 36(2). — Р. 507—517. — DOI: 10.1016/0017-9310(93)80025-P.
20. Ricci D., Manca O., Manca S., Nardini S. Two-Dimensional Numerical Investigation on Forced Convection in Channels With Transversal Ribs // Conference: ASME 2009 International Mechanical Engineering Congress and Exposition, IMECE2009. — 2009. — DOI: 10.1115/IMECE2009-11203.
21. Chaube A., Sahu P.K., Solanki S.C., Sharma P.B. Effect of Artificial Roughness on Convective Heat Transfer // 40th Thermophysics Conference. — 2008. — DOI: 10.2514/6.2008-3810.
22. Ahn S,W., Son K.P. An investigation on friction factors and heat transfer coefficients in a rectangular duct with surface roughness // KSME International Journal. — 2002. — № 16(4). — Р. 549—556.
23. Kant K., Qayoum A. Numerical investigations of fluid flow and heat transfer in a ribbed heated duct with variable aspect ratios // Recent Trends in Fluid Mechanics. — 2016. — V. 3. — Iss. 1. — Р. 23—37.
24. Kim J.-H., HeoSung-Hoo J.-N., Jeeyoung S. Numerical analysis on heat transfer and pressure drop characteristics in a horizontal channel with various ribs // DOI: 10.5916/jkosme.2013.37.1.40.
25. Smith E., Wayo C. Analysis of turbulent heat transfer and fluid flow in channels with various ribbed internal surfaces // Journal of Thermal Science. — 2011. — № 20(3). — Р. 260—267. — DOI: 10.1007/s11630-011-0468-3.
26. Naveen S., Andallib T., Manish M. Experimental Investigation of Heat Transfer Enhancement in Rectangular Duct with Pentagonal Ribs // Heat Transfer Engineering. — 2017. — DOI: 10.1080/01457632.2017.1421135.
27. Layek А., Saini J.S., Solanki S.C. Heat transfer and friction characteristics for artificially roughened ducts with compound turbulators // International Journal of Heat and Mass Transfer. — 2007. — № 50(23-24). — Р. 4845—4854. — DOI: 10.1016/j.ijheatmasstransfer.2007.02.042
28. Mohammed H.A., Abbas A.K., Sheriff J.M. Influence of geometrical parameters and forced convective heat transfer in transversely corrugated circular tubes // International Communications in Heat and Mass Transfer. — 2013. — DOI: 10.1016/j.icheatmasstransfer.2013.02.005.
29. Buonomo B., Cirillo L., Manca O., Nardini S. Experimental Investigation on Heat Transfer Enhancement by Transversal Ribs in Channels // ASME 2017 International Mechanical Engineering Congress and Exposition. — 2017. — DOI: 10.1115/IMECE2017-72032.
30. Tanda G., Abram R. Forced Convection Heat Transfer in Channels With Rib Turbulators Inclined at 45 deg // Journal of Turbomachinery. — 2009. — Арril. — V. 131 (2). — DOI: 10.1115/1.2987241.
31. Thikane S.J., Patil S.R. Review of Forced Convection Heat Transfer through Rectangular or Square Duct Provided with Different Configurations of Rib Turbulators // International Journal of Engineering and Technical Research. — 2015. — November. — V. 4 (11). — DOI: 10.17577/IJERTV4IS110135.
32. Dhaidan N., Abbas A.K. Turbulent forced convection flow inside inward-outward rib corrugated tubes with different rib-shapes // Heat Transfer-Asian Research. — 2018. — August. — DOI: 10.1002/htj.21365.
33. Cavallero D., Tanda G. An experimental investigation of forced convection heat transfer in channels with rib turbulators by means of liquid crystal thermography // Experimental Thermal and Fluid Science (EXP THERM FLUID SCI). — 2002. — June. — V. 26 (2). — DOI: 10.1016/S0894-1777(02)00117-6.
34. Jowkar M. Developing Heat Transfer in Rectangular Channels with Rib-Turbulators. — 2019. — August. — DOI: 10.22214/ijraset.2019.8044.
35. Manca O., Nardini S., Ricci D. Numerical investigation of air forced convection in channels with differently shaped transverse ribs // International Journal of Numerical Methods for Heat and Fluid Flow. — 2011. — June. — V. 21 (5). — P. 618—639. — DOI: 10.1108/09615531111135864.
36. Tanda G. Effect of Rib Spacing on Heat Transfer and Friction in a Rectangular Channel with 45-Deg Angled Rib Turbulators on One/Two Walls // International Journal of Heat and Mass Transfer. — 2011. — February. — V. 54 (54). — P.: 1081—1090. — DOI: 10.1016/j.ijheatmasstransfer.2010.11. 015.
37. Hamed M.S. Turbulence Modeling of Forced Convection Heat Transfer in Two-Dimensional Ribbed Channels // Journal of Electronic Packaging. — 2008. — January. — V. 130 (3). — DOI: 10.1115/1.2912182.
38. Al-Kayiem H., Ekhwan A.B., Muhi L.N. Augmentation of ribs turbulators height on the hydrothermal performance of double pipe heat exchanger // Journal of Engineering Science and Technology. — Vol. 12. — February. — №. 2 (2017). — Р. 548—563.
39. Manca O., Nardini S., Ricci D. Enhancement of Forced Convection in Ribbed Channels by Nanofluids Applied Thermal Engineering // Nanouptake COST Action. — 2012. — November. — V. 37. — P. 280—292. — DOI: 10.1115/IMECE2012-88892.
40. Wilkie D. Forced convection heat transfer from surfaces roughened by transverse ribs // International Heat Transfer Conference 3. — 2019. — January. — DOI: 10.1615/IHTC3.1540.
41. Tariq A., Sharma N., Manish M. Aerothermal Characteristics of Solid and Slitted Pentagonal Rib Turbulators // Journal of Heat Transfer. — 2018. — February. — V. 140 (6): 061901. — DOI: 10.1115/1.4039398.
42. Wong T.T., Leung C.W., Li Zeng-Yao, Tao Wen-Quan Turbulent convection of air-cooled rectangular duct with surface-mounted cross-ribs // International Journal of Heat and Mass Transfer. — 2003. — November. — V. 46 (24). — P.: 4629—4638. — DOI: 10.1016/S0017-9310(03)00298-9.
43. Joulin A., Cherif Y.C., Zalewski L., Rousse D.R. Turbulent forced convection in a horizontal channel with rectangular obstacle. — DOI: 10.1615/ICHMT.2008.CHT.1190.
44. Zhang M., Singh P., Ekkad S.V. Rib Turbulator Heat Transfer Enhancements at Very High Reynolds Numbers // Journal of Thermal Science and Engineering Applications. — 2019. — April. — V. 11 (6):1. — DOI: 10.1115/1.4043465.
45. Zeng Jia, Min LiuJian, Yu GaoTie, Jun Shi GaoJiao Heat Transfer in Narrow Rectangular Channels with Rib Turbulators. — 2011. — October. — DOI: 10.4028/www.scientific.net/AMR.354-355.1245.
46. Park J., Park S., Ligrani P. M. Numerical predictions of detailed flow structural characteristics in a channel with angled rib turbulators // Journal of Mechanical Science and Technology. — 2015. — November. — V. 29 (11). — P. 4981—4991. — DOI: 10.1007/s12206-015-1046-5.
47. Mehta Y.T., Ricklick M.A. CFD Benchmarking of Heat Transfer Predictions in Internal Channel with Rib Turbulators // 51st AIAA/SAE/ASEE Joint Propulsion Conference. — 2015. — July. — DOI: 10.2514/6.2015-3734
48. McMillin R. Turbulent heat transfer and friction in a square channel with discrete rib turbulators // Source OAI. — 1991. — January.
49. Safikhani H., Smith E. Multi-Objective Optimization of Turbulent Tube Flows Over Diamond-Shaped Turbulators // Heat Transfer Engineering. — 2016. — February. — V. 37 (18). P.: 1—25. — DOI: 10.1080/01457632.2016. 1151304.
Smith E., Promvonge P. Thermal characteristics of turbulent rib-grooved channel flows // International Communications in Heat and Mass Transfer. — 2009. — August. — V. 36 (7). — P.: 705—711. — DOI: 10.1016/ j.icheatmasstransfer.2009.03.025.
50. Smith E., Promvonge P. Thermal characterization of turbulent tube flows over diamond-shaped elements in tandem // International Journal of Thermal Sciences. — 2010. — June. — V. 49 (6). — P.: 1051—1062. — DOI: 10.1016/j.ijthermalsci.2009.12.003.
51. Kwon Hyuk-Jin, Wu Seong-Je, Cho Hyung-Hee Effects of Discrete Rib-Turbulators on Heat/Mass Transfer Augmentation in a Rectangular Duct // Transactions of the Korean Society of Mechanical Engineers. — 2000. — January. — V. B 24 (5).
52. Waghole D. Experimental and numerical investigation on heat transfer augmentation in a circular tube under forced convection with annular differential blockages/inserts // Heat and Mass Transfer. — 2018. — January. — V. 54 (6). — DOI: 10.1007/s00231-018-2276-8.
53. Ермаков В.И., Шеин В.С. Ремонт и монтаж химического оборудования. — Л.: Химия, 1981. — 367 с.
54. Поникаров И.Ш. Машины и аппараты химических производств. — М.: Машиностроение, 1989. — 368 с.

Рецензии:

31.05.2021, 18:16 Мирмович Эдуард Григорьевич
Рецензия: Это что, заправка окислителем ракет? Где это применяется? Рецензент любопытствует (а, может, и другой читатель) в какой области производства важно учитывать такие тонкости в перекачке такой агрессивной среды, каковой является азотная кислота. Из ссылок, включая зарубежные, также про HNOз не удаётся узнать. Игорь Евгеньевич и ранее в своих нескольких десятках работ на тему движения жидкостей в трубах не баловал нас этой информацией (что и для чего). Так что об актуальности данной работы что-то сказать трудно. Научный формат работы выдержан на самом высоком уровне. Редко встречается множественное числов в словосочетании "математическое моделирование", т.к. множественность чаще в объект моделирования переносится. Рецензент рекомендует работу к печати, если даже автор не захочет что-то учяесть из его пожеланий. Журнал очень выигрывает от цикла работ д-ра Лобанова И.Е.

4.06.2021, 13:01 Ашрапов Улугбек Товфикович
Рецензия: Общеизвестно, что азотная кислота используется для химической очистки теплообменников. Азотная кислота — сильная одноосновная кислота. Твёрдая азотная кислота образует две кристаллические модификации с моноклинной и ромбической решётками. Актуальность работы и задачи исследования не понятны, хотя изложены обширные расчетные данные.



Комментарии пользователей:

Оставить комментарий