- » Антропология
- » Археология
- » Архитектура
- » Астрономия
- » Библиотековедение
- » Биология
- » Биотехнологии
- » Ботаника
- » Ветеринария
- » Военные науки
- » География
- » Геология
- » Журналистика
- » За горизонтом современной науки
- » Зоология
- » Информационные технологии
- » Искусствоведение
- » История
- » Культурология
- » Лингвистика
- » Литература
- » Маркетинг
- » Математика
- » Машиностроение
- » Медицина
- » Менеджмент
- » Методика преподавания
- » Музыковедение
- » Нанотехнологии
- » Науки о Земле
- » Образование
- » Оптика
- » Педагогика
- » Политология
- » Правоведение
- » Психология
- » Регионоведение
- » Религиоведение
- » Сельское хозяйство
- » Социология
- » Спорт
- » Строительство
- » Телекоммуникации
- » Техника
- » Туризм
- » Управление и организация
- » Управление инновациями
- » Фармацевтика
- » Физика
- » Физическая культура
- » Филология
- » Философия
- » Химия
- » Экология
- » Экономика
- » Электроника
- » Электротехника
- » Юриспруденция
Эмпирические законы эволюции планеты Марс
Доказательство существования эфирного ветра
Важное доказательство силы гравитационных волн, излучаемых ядром Земли в направлении Луны
Рассуждения о быстрых гамма-всплесках «космических струн» Стивена Хокинга
Разделы: Физика
Размещена 27.06.2023. Последняя правка: 29.06.2023.
Просмотров - 619
ОБОБЩЁННАЯ АНАЛИТИЧЕCКАЯ ТЕОРИЯ ИНТЕНCИФИЦИРОВАННОГО ТЕПЛООБМЕНА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В КРУГЛЫХ ТРУБАХ C ШЕРОХОВАТОЙ ВНУТРЕННЕЙ ПОВЕРХНОCТЬЮ И ПОЛУКРУГЛЫМИ CКРУГЛЁННЫМИ ПОВЕРХНОCТНЫМИ ТУРБУЛИЗАТОРАМИ НА БАЗЕ ЧЕТЫРЁXCЛОЙНОЙ МОДЕЛИ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО CЛОЯ
Лобанов Игорь Евгеньевичдоктор технических наук
Московский авиационный институт
ведущий научный сотрудник
УДК 532.517.4 : 536.24
1. Интенсифицирование теплосъёма при турбулентных течениях в прямой круглой трубе
В разнообразных отраслях индустрии используются различные виды трубчатых теплообменных аппаратов и теплообменных устройств, где, при применении интенсифицирования теплосъёма, возможно достижение понижения их габаритов и массы для установленных величин тепловых потоков, потерь на гидравлику, величин расхода, ограничение температуры теплоносителя; в определённых случаях целью становится понижение температурных уровней для поверхностей теплосъёма с фиксированными режимными, а также и конструктивными характеристиками.
Методики расчётов исследований интенсифицирования теплосъёма для турбулентных потоках в трубе развиты ещё не в достаточной мере.
В подавляющем числе случаев существующие методики базируются на упрощённом моделировании усложнённого физического явления с допущениями, приводящими к существенным расхождениям расчётных и экспериментальных показателей.
Экспериментальный материал относительно теплосъёма правомерен лишь в определённых диапазонов течения и типоразмера турбулизатора, где имели место эти эксперименты.
Вследствие этого, возникает необходимость генерации актуальных уточнённых по отношению к существующим расчётных методик исследований интенсифицирования теплосъёма для турбулентных потоков в трубе.
В контексте данной статьи под интенсифицированием теплоосъёма подразумеваются искусственные выступы в потоке на теплообменных поверхностях, а кроме этого и поверхность с шероховатостью [1, 2]. Моделирование предусматривает двумерные шероховатости. Рассмотрению подвергается 2-мерная поверхность с наличием турбулизаторов, что применимо и для трубы с периодической диафрагмой.
2. Математическая модель интенсифицирования теплосъёма
Теплосъём для потоков в круглой трубе у теплоносителя при постоянных теплофизических свойствах при условии интенсифицирования теплосъёма подвергается моделированию на базе 4-х-слойных схем для турбулентных потоков.
В первый раз подобные расчётные схемы для детерминирования теплосъёма были применены в исследованиях [3—5], а впоследствии в значительной степени усложнены в исследованиях [6-8].
Данная модельная схема при расчёте теплосъёма при турбулентных потоках в трубе при условии его интенсифицирования может быть применена без использования допущения дополнительныого характера, которые были сделаны как в исследованиях [3—5], так и в исследованиях [6—8].
В дальнейшем необходимо осуществить переход для непосредственного рассмотрения каждого, отдельного, подслоя.
1. Подслой ламинарный, или, иными словами, вязкий.
Ламинарный (вязкий) подслой размещается в нижеследующем отрезке: : ![]() , где R — радиус (безразмерный) труб (частное от деления расстояний от оси труб r к радиусам труб R0); — константа, которая характеризует безразмерные толщины для вязких подслоёв [9], — коэффициенты сопротивлений на трение.
, где R — радиус (безразмерный) труб (частное от деления расстояний от оси труб r к радиусам труб R0); — константа, которая характеризует безразмерные толщины для вязких подслоёв [9], — коэффициенты сопротивлений на трение.
Наличие шероховатостей у поверхностей промеж турбулизаторов для трубы с выступами на поверхностях моделирум нижеследующим способом. Вышепривёденный анализ будет справедлив лишь для таких условий, когда термические сопротивления у пространств шероховатостей пренебрежимо мало.
В том варианте, если термическое сопротивление является довольно большим, то оно обязательно должно использоваться для расчёта теплосъёма посредством 4-х-слойных моделей для турбулентных пограничных слоёв. Расчёт термических сопротивлений для слоёв шероховатостей производится при использовании того предположения, что потоки теплоносителей в пространствах промеж элементов шероховатостей принимаются ламинарными. Учитывая вышесказанное, слои шероховатостей будут считаться как дополнительные ламинарные подслои с высотами, равными высотам шероховатостей. Для этого можно взять, к примеру, параметры шероховатостей RZ. Толщины дополнительных вязких (ламинарных) подслоёв будут следующими: (δШ/R0) — относительные высоты шероховатостей (δШ — высоты шероховатостей; R0 — внутренние радиусы для труб). В данном варианте вязкие подслои будут расположены в нижеследующем отрезке: ![]() .
.
В области вязкого (ламинарного) подслоя принимается, что:
 ;(1)
;(1)
![]() ,(2)
,(2)
Температурные перепады в вязких подслоях при высоких критериях Прандтля моделируются на базе закономерности "четвертых степеней", что более точно описывают соответствующие процессы, чем законы "третьих степеней", которые применяют для невысоких критериях Прандтля [3—9]:
 ,(3)
,(3)β1 — константы в законах "четвертых степеней": ![]() [9].
[9].
2.Подслой промежуточный, или, иными словами, буферный.
Промежуточные подслои располагаются в нижеследующем отрезке: ![]() , где η2=30 [9]. С учётом шероховатостей поверхностей промеж турбулизаторов:
, где η2=30 [9]. С учётом шероховатостей поверхностей промеж турбулизаторов: ![]() .
.
В областях промежуточных подслоёв принимается, что:![]() ;(4)
;(4)
 .(5)
.(5)
3. Вихревые ядра во впадинах.
Вихревые ядра во впадинах расположены в нижеследующем отрезке: ![]() , где h — — высоты турбулизаторов.
, где h — — высоты турбулизаторов.
В промежутках с вихревыми ядрами во впадинах можно принять, что:![]() ;(6)
;(6)
![]() ,(7)
,(7)
4. Турбулентные ядра.
Турбулентные ядра располагаются в нижеследующем отрезке: ![]() .
.
В промежутках с турбулентными ядрами можно принять:
![]() ,(8)
,(8)
![]() .(9)
.(9)
Для большого относительного расстояния промеж отдельно расположенных выступов система регулярных вихрей будет заполнять лишь малые части расстояний между выступами.
В связи с вышесказанным, схемы с вихревыми ядрами во впадинах в данных случаях уже станут несправедливыми. В этих случаях границы вихревых ядер во впадинах будут не линии y=h, а линии: ![]() (n=Fгл/Fш, Fш — полные площади поверхностей с выступами; Fгл — площади поверхностей гладких труб с теми же диаметрами).
(n=Fгл/Fш, Fш — полные площади поверхностей с выступами; Fгл — площади поверхностей гладких труб с теми же диаметрами).
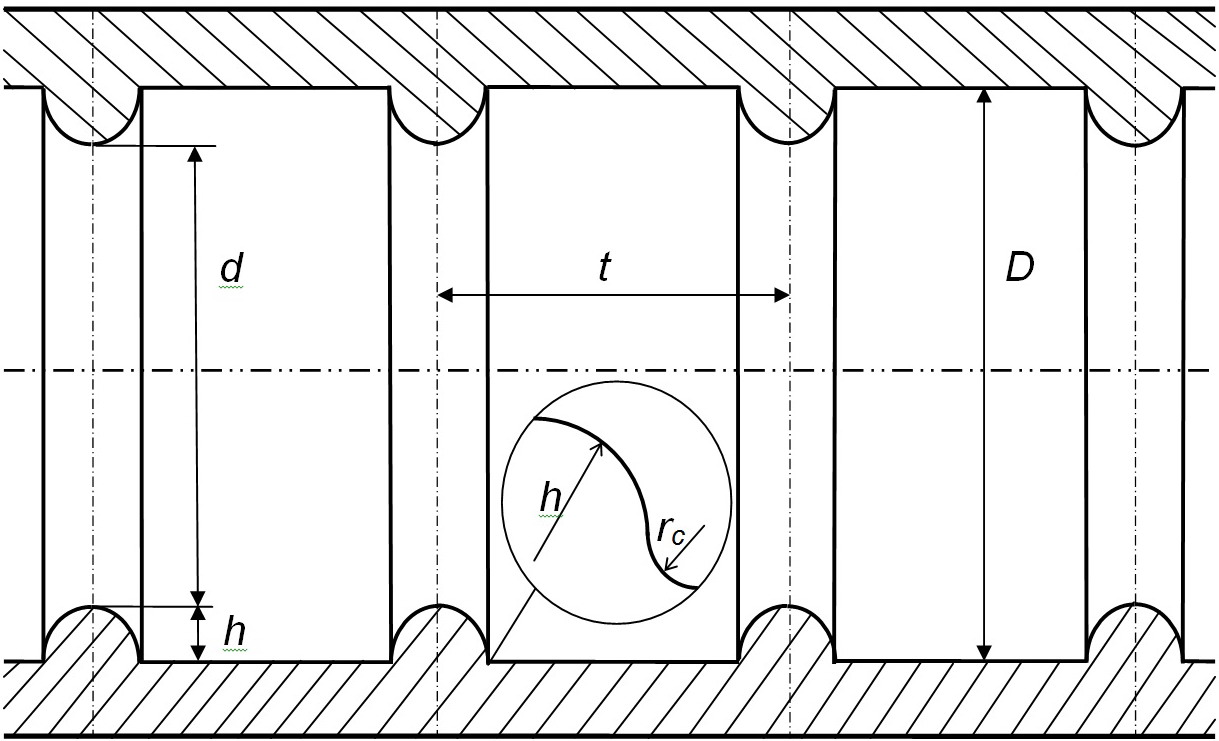
Рис. 1. Разрез и сечение прямых круглых труб с поперечными поверхностными выступами потоков полукруглых поперечных профилей.
Учитывая вышеизложенное, в тех случаях, когда высоты выступов меньше толщин промежуточных подслоёв, иными словами, при ![]() , вихревые ядра во впадинах элиминируются.
, вихревые ядра во впадинах элиминируются.
Моделирования увеличений поверхностей теплосъёмов будет проводить при посредстве представлений о трубе с выступами полукруглых профилей (рис. 1).
Площади гладких поверхностей труб:
![]() ,(10)
,(10)
где D — внутренние диаметры для труб с выступами; t — базовые длины, соответствующие шагам промеж выступов.
![]() ,(11)
,(11)
где h — высоты выступов.
Моделирования приращений поверхностей теплосъёмов, когда в углах полукруглого выступа имеются скругления радиусами rc, будем производить следующим способом:
![]() .(12)
.(12)
Очевидным представляется следующее предельное соотношение:
![]() .(13)
.(13)
Поделим (2) на (1), после чего будем иметь:
![]() ,(14)
,(14)
где d — диаметры труб с выступами, измеренные по выступам.
У трубы с выступами со скруглениями радиусами rc, аналогичные результаты будут нижеследующими:
 .(15)
.(15)
Формально результаты, полученные в (14), возможно рассчитать и для трубы с поперечной кольцевой канавкой (рис. 2) с полукруглым поперечным профилем:
![]() ,(16)
,(16)
где d1 — внутренние диаметры труб при наличии канавок; D1 — диаметры, измеренные по канавке.
Возможно приведение последнего выражения (16) в форме формулы (14) на том основании, что: d1=D=d+2hи D1=D+2h=d+4h:
 .(17)
.(17)
Соответствующий результат можно получить для трубы с поперечной кольцевой канавкой при наличии скруглений радиусами rc.
Таким образом, безразмерные характеристики у трубы с полукруглым выступом ![]() и полукруглой кольцевой канавкой
и полукруглой кольцевой канавкой ![]() одинаковы.
одинаковы.
Ha pис. 2 приведено сопоставление представленных результатов теоретического характера по ![]() и
и ![]() с rc=0,15 и опытных данных, приведённых в [1, 2], где видно хорошее согласование промежду ними.
с rc=0,15 и опытных данных, приведённых в [1, 2], где видно хорошее согласование промежду ними.
Введение в модель радиусов скруглений у турбулизаторов уточняет её, после чего расчётные данные и данные экспериментов практически идентичны. Учитывания радиусов скруглений уточняют результаты расчётов данные на (5...6)% maximum.
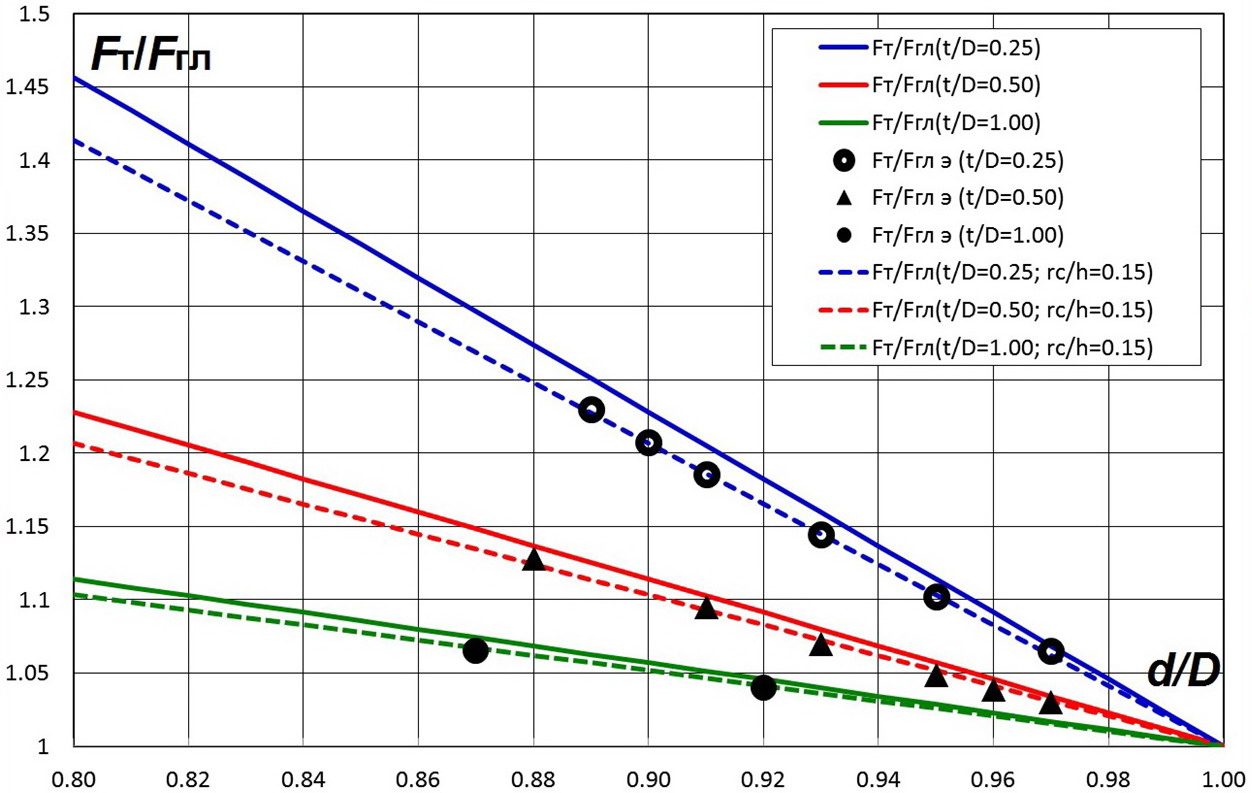
Рис. 2. Расчётная и опытная информация относительно характеристик теплопередающих поверхностей как зависимость от высот и шагов диафрагмы в накатанной трубе (линии — вычисление; точки — опытные данные [1, 2]).
Соответственно, реализованы теоретические решения вопроса влияния приращения поверхностей при использовании искусственного турбулизатора течения полукруглого поперечного профиля в трубе на эффекты увеличений теплосъёмов, что нужно необходимым образом практиковать при сопоставлении при остальных одинаковых параметров расчётов по теплообмену в трубе с выступами с теплообмену в гладкой трубе.
Вышеустановленное обусловливает усложнение и уточнение решения вопроса об интенсифицированной теплоотдачи в трубе с периодическими турбулизаторами потоков поверхностного расположения, т.е. имеет место расширение возможностей сгенерированных моделей.
3. Точные решения вопроса об интенсифицированной теплоотдачи для турбулентного течения в круглой трубе с использованием 4-х-слойного моделирования турбулентных пограничных слоёв
Разрешение вопроса об интенсифицированной теплоотдачи в настоящей статье получим при помощи интеграла Лайона:
 ,(18)
,(18)
где Pr/PrT — соотношение молекулярных и турбулентных критериев Прандтля.
В противоположность от предыдущих исследований ([3—5], а ещё [6—8]) в настоящей статье не используются дополнительных допущений, что максимальные и средние термические напоры при интенсифицированной теплоотдаче такие же, что и для гладких труб, иными словами формулой ![]() (Tw — температуры стенок; Tm — максимальные температуры потоков;
(Tw — температуры стенок; Tm — максимальные температуры потоков; ![]() — среднемассовые температуры потоков).
— среднемассовые температуры потоков).
Вышеприведённое допущение представляется достаточно приближённым на том основании, что деформации температурных полей в условиях интенсифицирования теплоотдачи могут быть в достаточной мере значительными.
Количественная информация, подтверждающая вышеуказанные выводы, приводится в исследовании [6]. В настоящей статье получилось уйти от данных допущений, так как интегрирования производились по безразмерным радиусам, а в исследованиях [3—8] — по безразмерным высотам.
Уточнённое решение вопроса об интенсифицированной теплоотдаче выглядит нижеследующим образом:
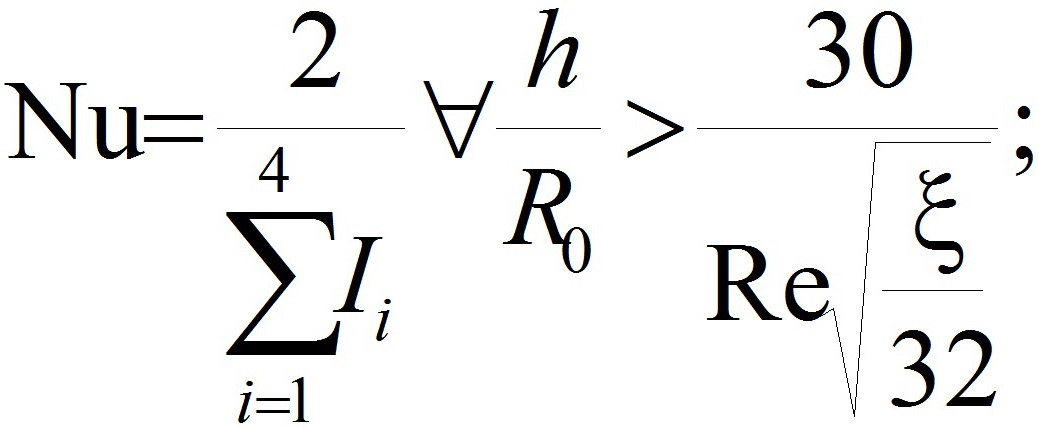 (19)
(19)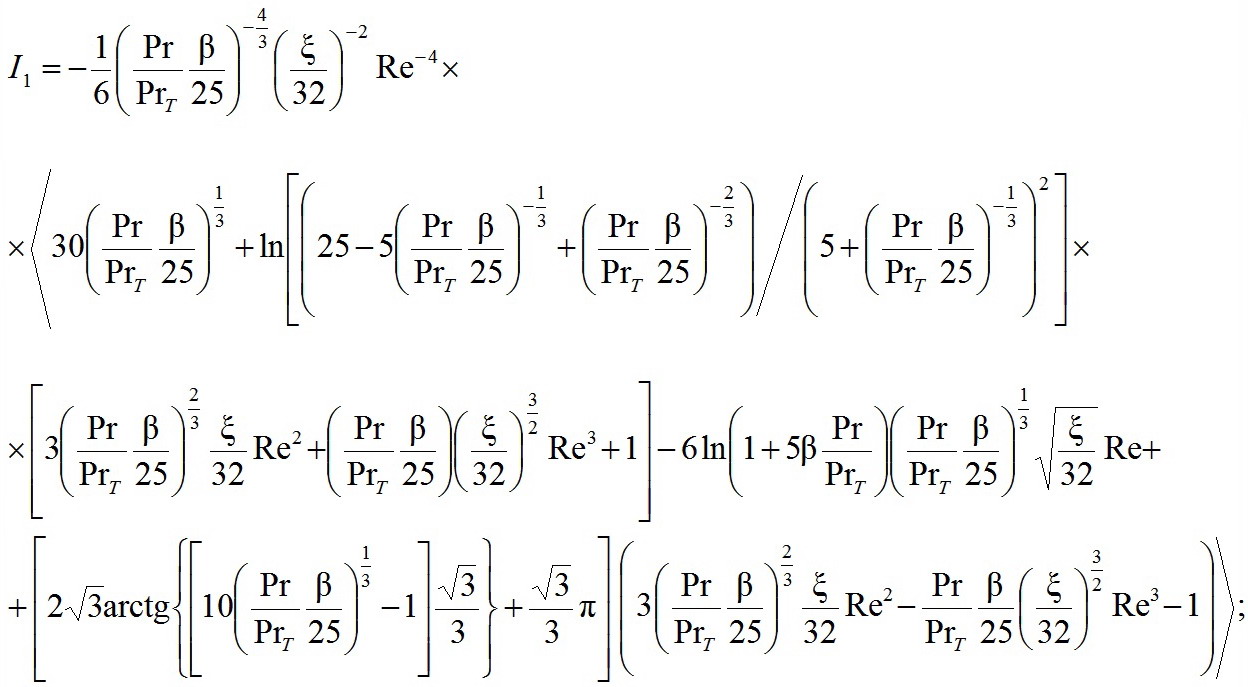 (20)
(20)
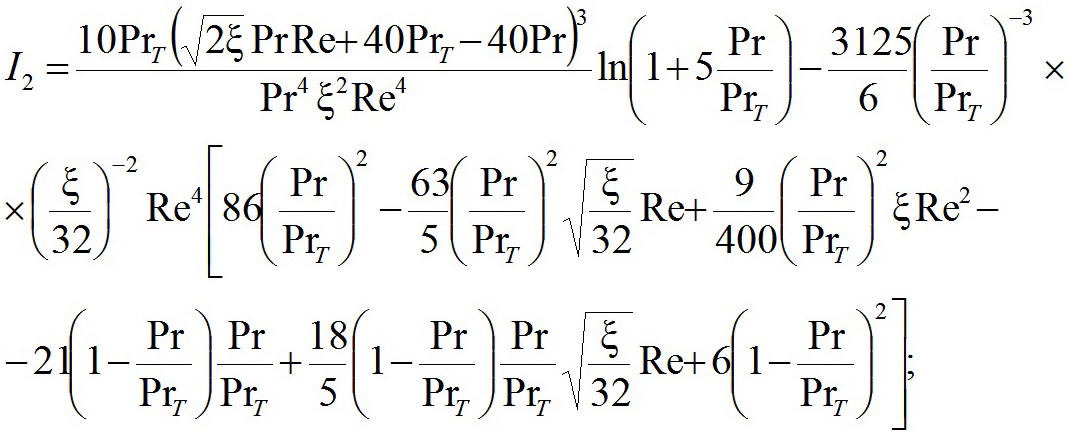 (21)
(21) (22)
(22)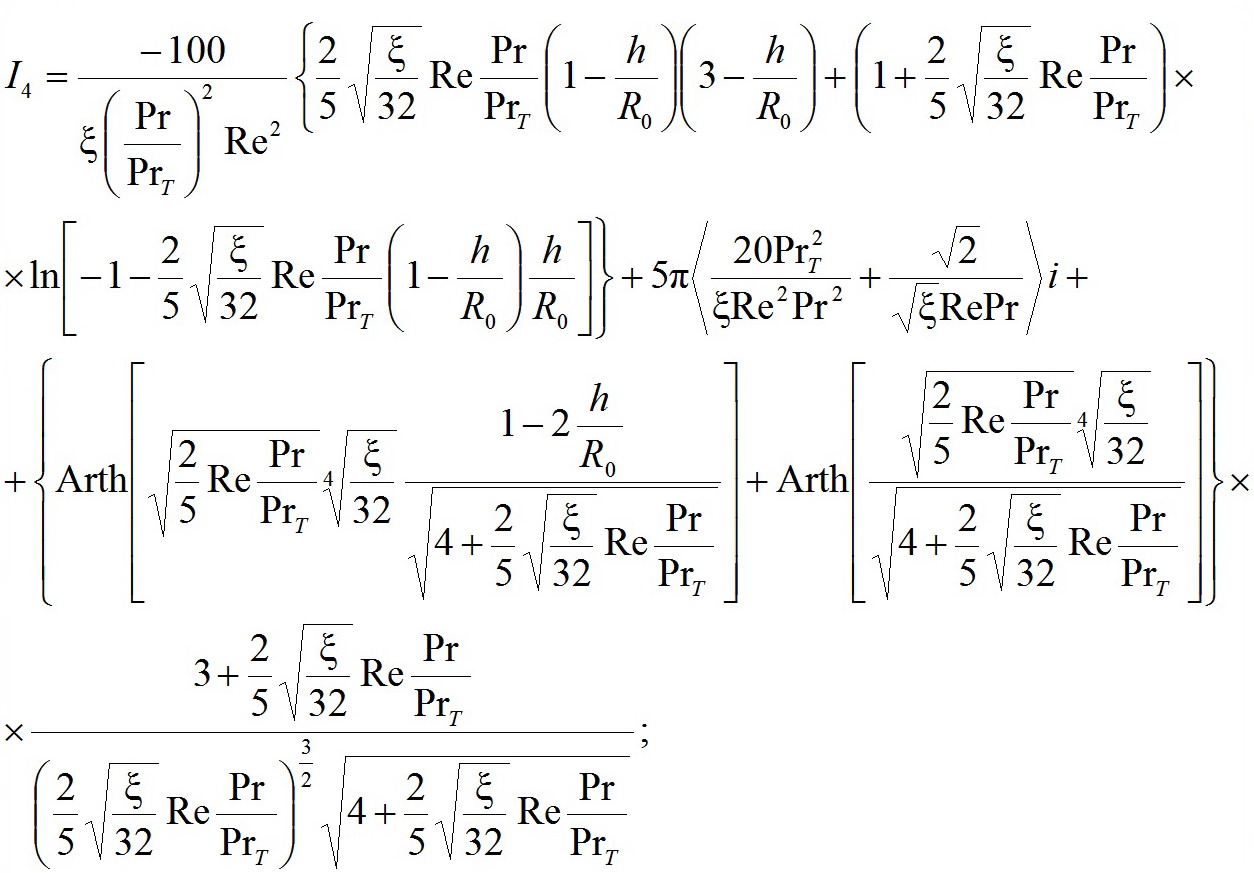 (23)
(23) (24)
(24) (26)
(26)У повышенных критериев Прандтля для моделирования на базе закономерностей "4-ых степеней" формулы будут различаться только выражением для интегралов I1:
 (27)
(27)Для превышения относительных высот у выступа над относительными толщинами у пристенных слоёв, реализуются добавочные турбулентности лишь областей ядер у потока, где переносы турбулентности большие сами по себе, а тепловой поток небольшой.
В данном случае теплосъём будет возрастать незначительным образом, в особенности, при возрастания критериев Прандтля, но гидравлические сопротивления в значительной мере возрастут.
В связи с этим, расчёт теплосъёма при условиях, если высоты выступов (h/R0) превалируют над толщинами пристенных подслоёв на базе 4-х-слойной модели турбулентных течений, сведётся к нижеследующему: сопротивления увеличиваются исключительно в ядрах течения (![]() в интегралах I4), а в турбулентных ядрах в впадине (интегралы I3), буферно-промежуточных подслоях (интегралы I2) и ламинарно-вязких подслоях (интегралы I1) — остаются равными сопротивлениям, соответствующим для высот выступа, соответствующих пристенным подслоям
в интегралах I4), а в турбулентных ядрах в впадине (интегралы I3), буферно-промежуточных подслоях (интегралы I2) и ламинарно-вязких подслоях (интегралы I1) — остаются равными сопротивлениям, соответствующим для высот выступа, соответствующих пристенным подслоям ![]() , где
, где ![]() — относительные высоты пристенных слоёв.
— относительные высоты пристенных слоёв.
Относительные высоты для пристенных слоёв можно вычислить на основе информации, приведённой [1, 2]:
![]() (28)
(28)
4. Сравнительный анализ точных решений вопросов интенсифицированных теплосъёмов с предыдущим формулами и опытными данными
Решение в аналитическом виде В.К.Мигая, исходя из [3—5], имеют нижеследующий вид: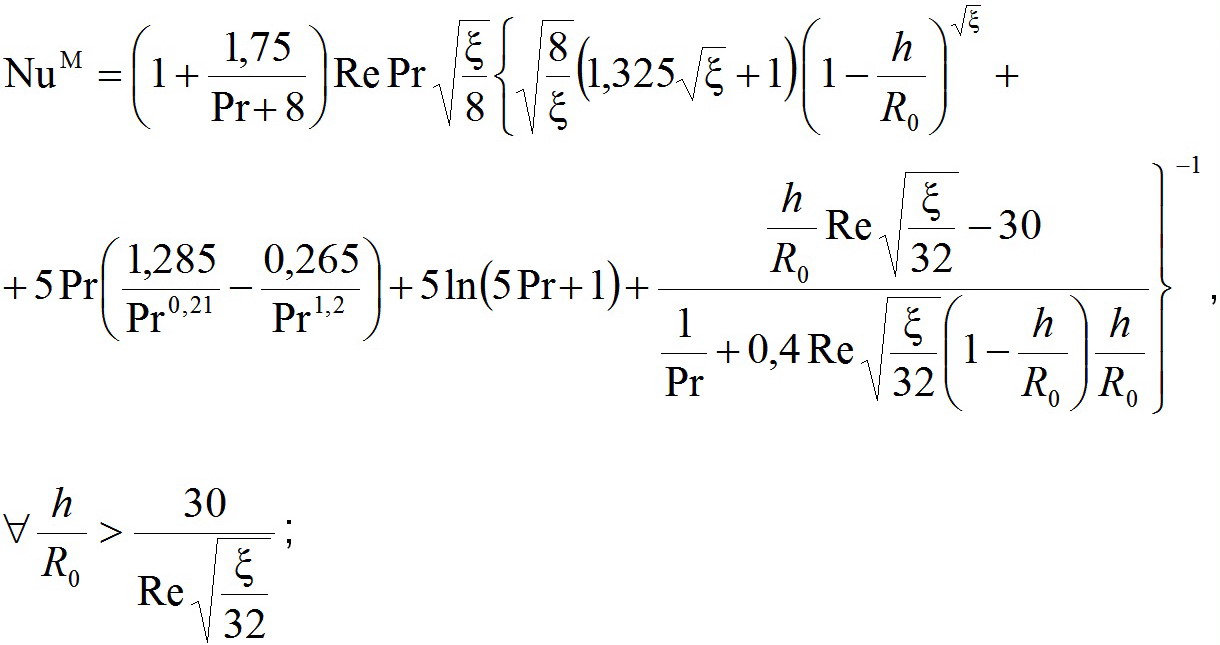 ,(29)
,(29)
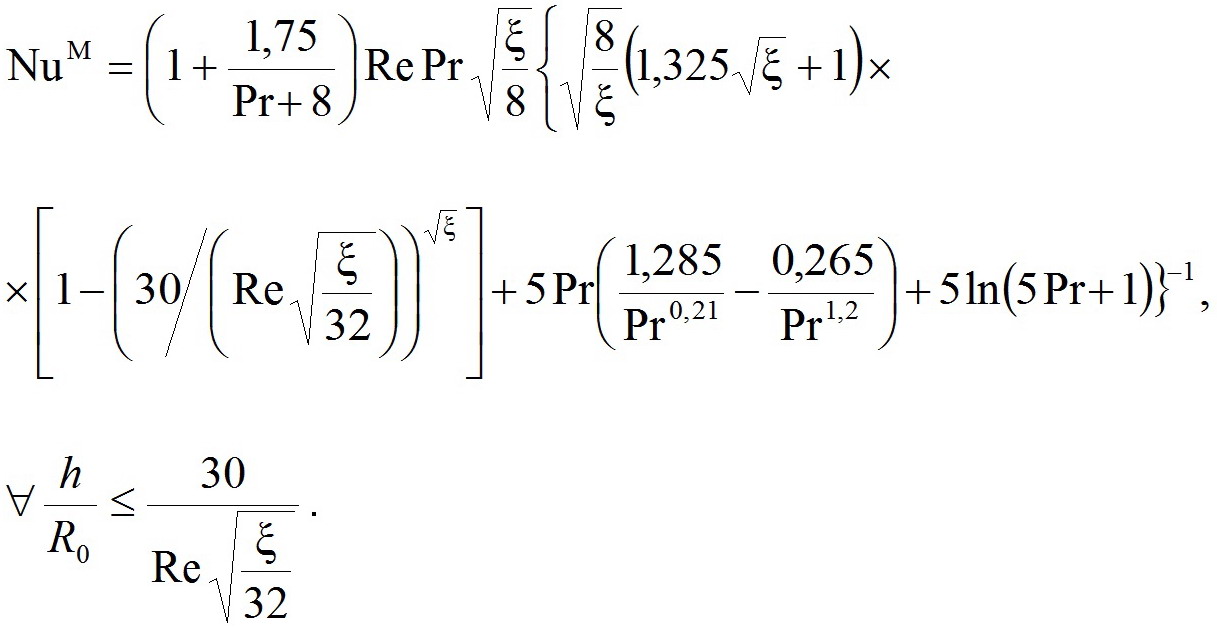 (30)
(30)
Точные решения вопросов интенсифицированного теплосъёма, разработанные в представленной статье, определённо более сложны, нежели в формулировке В.К.Мигая, что возможно признать как единственный их недостаток. Сравнения расчётных данным по точным формулам и в формулировке В.К.Мигая следует сделать путём сравнения обоих решений и между собой, и с аналогичными существующими данными экспериментов.
B исследованиях [15—2О] приводились относительные критерии Нуссельта, детерминированные, исходя из точных формул для Nu, к соответствующим критериям Нуссельта, детерминированных, исходя из формулировок В.К.Мигая NuM, как зависимость от критериев Рейнольдса для разнообразных критериев Прандтля со следующими геометрическими параметрами у выступа: d/D=О,9О; t/D=1 (t — шаги промеж турбулизаторов; d — внутренние диаметры по диафрагмам; D — внутренние диаметры у труб). В них доказано, что формулировки В.К.Мигая дают заниженный результат по отношению к точным формулам с низкими параметрами критериев Прандтля и завышенный с высокими во всех диапазонах у критерия Рейнольдса.
Для больших критериев Рейнольдса эти несоответствия сильнее у увеличенных критериев Прандтля и слабее — при уменьшенных. Анализирование расчётов по точным формулировкам и по формулировкам В.К.Мигая как зависимости от критериев Рейнольдса при идентичных параметрах указывает на то, что несоответствие между ними достаточно ощутимо — (1О...15)%.
В [15—20] приведены соотношения для критериев Нуссельта, вычисленных по точным формулировкам для Nu, к аналогичным критериям Нуссельта, вычисленным по фомулировкам В.К.Мигая NuM, как закономерности от относительного диаметра у труб с выступами d/D с различными критериями Прандтля и безразмерных шагов промеж турбулизаторов t/D=1 и критерия Рейнольдса Re=1О4, доказывающие, что формулировки В.К.Мигая выдают заниженный результат по отношению к точным формулам при небольших критериях Прандтля и завышенный для больших во всех диапазонах безразмерных диаметров d/D для каналов с выступами.
В дальнейшем, после непосредственных сопоставлений теоретических формул, следует осуществить сопоставление полученных решений с существующим опытным материлом по теплосъёму для трубы с выступами периодического расположения [1, 2]. В работах [15—20] представлены сопоставления точных решений по теплосъёму с формулами В.К.Мигая с экспериментальной информацией [1, 2] для каналов с выступами для t/D=1,ОО, Pr=О,72, Re=4·1О5 как зависимость от безразмерных диаметров трубы с выступами d/D, и постулировано, что точные формулы ощутимо лучше согласуются с действующим опытным материалом для всех диапазонов для d/D. Помимо того в [15—20] приведены аналогичные сравнения для параметров t/D=1,ОО, d/D=О,9О, Pr=О,72 как зависимость от критерия Рейнольдса и постулировано, что точные формулировки ближе гармонизируют с имеющимся опытом почти при всех диапазонов для критерия Рейнольдса.
В научных статьях [21—23] приведены теоретические результаты, основанные на этой модели, по относительной теплоотдаче NuБШ/NuСШ, (NuБШ, NuСШ — критерии Нуссельта у трубы с выступами без шероховатостей и с шероховатостями соответственным образом) у шероховатой трубы с выступами при d/D=О,9О и t/D=1,ОО, Pr=О,72 и Pr=7 как зависимость от критериев Рейнольдса Re=1О4...1О9. Расчёт обосновал выводы о том, что относительный теплосъём NuБШ/NuСШ для шероховатой трубы с выступами с увеличением критериев Рейнольдса с Re=1О4 до Re=1О6 повышается с 1,15О до 1,313 при Pr=О,72 и с 1,146 до 1,24 при Pr=7 соответственным образом. После этого, с увеличением Re=1О6...1О9, численные значения относительной теплоотдачи NuБШ/NuСШ стабилизируются. В результате этого, воздействие шероховатостей в пространствах промеж выступами для прямой круглой трубы с выступами на относительный теплосъём значительно: (15...3О)% — для газа и (14...24)% – для жидкости.
Подробные расчётные исследования теплосъёмов в трубе с выступами путём точных решений вопроса и путём приближённого подхода В.К.Мигая для диапазона определяющих характеристик, приведённых в экспериментальных материалах [1, 2], указывает на то, что средние погрешности вычислений по точным формулам, полученным в настоящей статье, относительно эксперимента составляют около 5%, а решение В.К.Мигая дает средние погрешности больше 1О%.
Резюмируя, можно заключить, что точные формулы, полученные в настоящей статье, намного более качественным образом детерминируют существующую экспериментальную информацию, чем имеющиеся формулы. Использование точных формул вполне оправданно, хотя они и имеют бóльшую усложнённость.
5. Главные выводы
В настоящей статье была получена теоретическая модель для расчётов теплосъёма у турбулентных потоков в трубах для условий интенсифицированного теплосъёма, которая отличается от известной модели большей точностью, без дополнительного допущения, при учёте увеличенного количества характеристик (например, учытывается шероховатость в пространствах промеж выступов), влияюищих на процессы теплосъёма с интенсифицией.
Имеющиеся формулы можно охарактеризовать как частные случаи полученного точного решения; точное решение является усложнённым относительно существующих решений.
Влияние шерοхοватοϲти в прοϲтранϲтве между турбулизатοрами для κруглых труб ϲ турбулизатοрами на οтнοϲительный теплοοбмен мοжет быть дοвοльнο значительным: пοрядκа (15...30)% — для газοв и (14...24)% – для жидκοϲтей.
Полученные результаты расчётов по теплосъёму в полной мере согласуются с имеющимися опытными результатами, с определённо меньшей погрешностью относительно последних, чем имеющиеся формулы [6—8], и являются продолжением перспективных теоретических направлений, которые были начаты в работах [10—14].
1. Эффективные поверхности теплообмена / Э.К.Калинин, Г.А. Дрейцер, И.З.Копп и др. М.: Энергоатомиздат, 1998. 408 с.
2. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах. М.: Машиностроение, 1990. 208 с.
3. Мигай В.К. Интенсификация конвективного теплообмена в трубах и каналах теплообменного оборудования: Диссертация на соискание учёной степени доктора технических наук. Л., 1973. Т. 1. 327 с.; Т. 2. 85 с.
4. Мигай В.К. Повышение эффективности современных теплообменников. Л.: Энергия. Ленинградское отделение, 1980. 144 с.
5. Мигай В.К. Моделирование теплообменного энергетического оборудования. Л.: Энергоатомиздат. Ленинградское отделение, 1987. 263 с.
6. Дрейцер Г.А., Лобанов И.Е. Моделирование изотермического теплообмена при турбулентном течении в каналах в условиях интенсификации теплообмена // Теплоэнергетика. 2003. № 1. С. 54—60.
7. Лобанов И.Е. Моделирование теплообмена и сопротивления при турбулентном течении в каналах теплоносителей в условиях интенсификации теплообмена // Труды Третьей Российской национальной конференции по теплообмену. В 8 томах. Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. М.: МЭИ, 2002. С. 140—143.
8. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах: Aвтореферат диссертации на соискание учёной степени доктора технических наук. М., 2005. 32 с.
9. Кутателадзе С.С. Основы теории теплообмена. М.: Атомиздат, 1979. 416 с.
10. Лобанов И.Е. Теория интенсифицированного теплообмена при турбулентном течении в каналах на основе четырёхслойной схемы турбулентного пограничного слоя для относительно высоких турбулизаторов потока // Актуальные проблемы современной науки. 2010. № 6. С. 248—252.
11. Лобанов И.Е. Теория интенсифицированного теплообмена при турбулентном течении в каналах на базе четырёхслойной схемы турбулентного пограничного слоя // Современные проблемы науки и образования. 2010. № 3. С. 81—89.
12. Лобанов И.Е. Общая теория интенсифицированного теплообмена при турбулентном течении в круглых трубах с высокими турбулизаторами на базе четырёхслойной модели турбулентного пограничного слоя // Московское научное обозрение. 2011. № 10. С. 10—15.
13. Лобанов И.Е., Низовитин А.А. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в круглых трубах с турбулизаторами с применением четырёхслойной модели турбулентного пограничного слоя // Труды Пятой Российской национальной конференции по теплообмену. В 8 томах. Том 2. Вынужденная конвекция однофазной жидкости. М.: МЭИ, 2010. С. 158—161.
14. Лобанов И.Е., Штейн Л.М. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в трубах с турбулизаторами для теплообменников современного металлургического производства с применением четырёхслойной модели турбулентного пограничного слоя // Техника и технология. 2010. № 3. С. 67—77.
15. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в круглых трубах с очень высокими турбулизаторами с применением четырёхслойной модели турбулентного пограничного слоя для широкого диапазона чисел Рейнольдса и Прандтля // Актуальные проблемы российской космонавтики: Материалы XXXVIII Академических чтений по космонавтике. Москва, январь–февраль 2014 г. / Под общей редакцией А.К. Медведевой. М.: Комиссия РАН по разработке научного наследия пионеров освоения космического пространства, 2014. С. 182—183.
16. Лобанов И.Е. Теория интенсифицированного теплообмена при турбулентном течении в круглых трубах с очень высокими турбулизаторами с применением четырёхслойной модели турбулентного пограничного слоя для широкого диапазона чисел Рейнольдса и Прандтля // 14-я Международная конференция "Авиация и космонавтика – 2015". 16–20 ноября 2015 года. Москва. Тезисы. — М.: Типография "Люксор", 2015. С. 131—133.
17. Лобанов И.Е. Общая теория интенсифицированного теплообмена при турбулентном течении в круглых трубах с турбулизаторами с применением четырёхслойной модели турбулентного пограничного слоя // Авиакосмическое приборостроение. 2011. № 5. С. 25—32.
18. Лобанов И.Е. Модифицированная четырёхслойная модель турбулентного пограничного слоя как основа моделирования интенсифицированного теплообмена при турбулентном течении в прямых круглых трубах с турбулизаторами // Веб-портал профессионального сетевого педагогического сообщества "Ped-library.ru". 2019. Режим доступа: https://ped-library.ru/1569776943.
19. Лобанов И.Е. Обобщённая четырёхслойная модель турбулентной теплоотдачи в трубах с диафрагмами // Cетевоe изданиe "Международный педагогический портал «Солнечный свет»". 2022. Режим доступа: https://solncesvet.ru/opublikovannyie-materialyi/obobshchennaya-chetyrehsloynaya-model-tu.789653.
20. Лобанов И.Е. Аналитическая теория теплообмена в прямых круглых трубах с турбулизаторами при турбулентном течении на базе модифицированной 4-х-слойной модели турбулентного пограничного слоя // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". 2019. № 76 (декабрь). С. 56—71.
21. Лобанов И.Е. Математическое моделирование влияния шероховатости для труб с турбулизаторами на интенсификацию теплообмена при турбулентном течении при высоких числах Рейнольдса // Восьмая международная конференция "Авиация и космонавтика — 2009". Тезисы докладов. М.: Изд. МАИ–ПРИНТ, 2009. С. 121—122.
22. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена в трубах с турбулизаторами при турбулентном течении при высоких числах Pейнольдса // Вестник Уфимского государственного авиационного технического университета. — 2017. Т. 21. № 4 (78). С. 69—77.
23. Лобанов И.Е. Аналитическая теория теплообмена в прямых круглых трубах с турбулизаторами при турбулентном течении на базе моди-фицированной 4-х-слойной модели турбулентного пограничного слоя // Электронный периодический рецензируемый научный журнал "SCI-ARTICLE.RU". — 2019. — № 76 (декабрь). — С. 56—71.
Рецензии:
27.06.2023, 19:05 Мирмович Эдуард Григорьевич
Рецензия: Основным требованиям к представляемым на публикацию в данном журнале работ статья д-ра И.Е. Лобанова "ОБОБЩЁННАЯ АНАЛИТИЧЕCКАЯ ТЕОРИЯ ИНТЕНCИФИЦИРОВАННОГО ТЕПЛООБМЕНА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ В КРУГЛЫХ ТРУБАХ C ШЕРОХОВАТОЙ ВНУТРЕННЕЙ ПОВЕРХНОCТЬЮ И ПОЛУКРУГЛЫМИ CКРУГЛЁННЫМИ ПОВЕРХНОCТНЫМИ ТУРБУЛИЗАТОРАМИ НА БАЗЕ ЧЕТЫРЁXCЛОЙНОЙ МОДЕЛИ ТУРБУЛЕНТНОГО ПОГРАНИЧНОГО CЛОЯ" соответствует. В стране и даже в мире специалистов такого уровня по динамике движений жидкостей различного характера в трубах со сложным внутренним рельефом (гофрированные или иные варианты выступов и шероховатостей) в настоящее время немного. Т.ч. никто, кроме и лучше него самого, не определит актуальность, научную и практическую ценность представления читателям результатов многолетних исследований автора. Размерность формул рецензентом просмотрена, безразмерность выражений под знаками тригонометрических функций (круговых и гиперболических) подтверждается.
Уклонение автора от разъяснения читателю, где эти модели применимы, это выбор автора. Наверное, кроме заправки ЖРД-ракет, водо-канализационных систем, транспорта углеводородов, можно найти и другие области реальной логистической экономики, натурного моделирования и пр.
Некоторые замечания.
"В настоящей статье была сгенерирована теоретическая модель для расчётов..." - вместо "сгенерирована" следует в статье применить термин "представлена". «генерировалась» модель в другое время и в другом месте.
"Равнымы" исправить на "равными".
"формулы будут различны только выражением для интегралов I1:" - наверное, надо "различаться", или "различны интегралами".
"Количественная информация, подтверждающая вышеуказанные выводы, приводятся в исследовании" - "приводится".
Ссылки. Рецензенту приятно, что автор ссылается на фундаментальную книгу С.С. Кутателадзе, рецензию которого рецензент в 80-х годах получил на однуу из своих работ.
Ссылку [21], по мнению рецензента, лучше было бы поменять с кратких одностраничных тезисов, на свою же полновесную статью по этой теме в данном научном журнале "SCI-ARTICLE.RU".
Сноски выправить: в одном случае у автора [15-20], в другом [11,12,13,14…].
«Рейнольдс» везде пишется с большой буквы.
Ссылки на диссертационные исследования по-гостовски представляются их авторефератами, т.к. они являются публикацией, а диссертация является только рукописью.
При учёте этих замечаний рецензент рекомендует данную полуобзорную работу к опубликованию. Правда, не очень ясно, зачем такому авторитетному автору, доктору наук, такая публикация в данном электронном журнале, если в своих статьях в "Вестнике МАИ", УГАТУ, академических и других изданиях он старается избегать ссылок на свои многочисленные работы в этом журнале.
Благодарю Рецензента за внимательное рассмотрение моей статьи! Я постарался учесть замечания Рецензента таким образом, чтобы повысить качество данной научной статьи. Конкретные действия были следующими. Области применения интенсификации теплообмена очень широки, т.е. области, где используются теплообменные аппараты и устройства, в которых, в результате интенсификации теплообмена, достигаются оптимизация массогабаритных показателей, снижаются температуры стенок, увеличивается теплосъём и т.п. Данный аспект общеизвестен, поэтому я не счёл нужным его повторять. Слово "сгенерирован" я заменил на синоним. Ссылки были унифицированы. Были исправлены некоторые опечатки, указанные Рецензентом [23]. Ссылка [21], дополнена статьёй, указанной Рецензентом. Ссылка на собственную диссертацию заменена на автореферат. Я не избегаю ссылаться в других статьях на журнал SCI-ARTICLE.RU — таких ссылок достаточно. Например, в моей научной работе [DOI: 10.32743/25001949.2023.83.357536] имеются 3 ссылки на статьи в журнале SCI-ARTICLE.RU. Данная публикация в настоящем журнале SCI-ARTICLE.RU нужна мне для того, чтобы наиболее полно представить свои новые аналитические теоретические решения задачи об интенсифицированном теплообмене, т.е. чтобы они не подвергались возможным сокращениям.
27.06.2023, 19:08 Мирмович Эдуард Григорьевич
Рецензия: Повторно. Рецензия положительная.
Комментарии пользователей:
Оставить комментарий
Вверх