Разделы: Математика
Размещена 01.11.2023. Последняя правка: 16.01.2024.
Просмотров - 501

Степени заполненности / незаполненности разрядов чисел. Великая теорема Харта. Хартовы тройки чисел

Харт Алекс

Индивидуальный предприниматель

Индивидуальный предприниматель

УДК 511

Введение

В работах [1] и [2] даны определения понятиям абсолютной и фактической заполненности разрядов чисел при записи их в той или иной системе счисления. А в работах [3] и [4] предложена математическая игра, в которой данные понятия используются в контексте силы или слабости чисел.

Актуальность

Дальнейшее исследование данного направления и данных понятий актуально. И следующим шагом на таком пути является связывание между собой понятия заполненнсти разрядов и степени числа, ввод понятия степени заполненности разрядов.

Цели

Ввести понятия степени заполненности и незаполненности разрядов чисел и показать связь этих понятий со степенью числа. Сформулировать на основе данных понятий гипотезу, аналогичную Великой теореме Ферма и гипотезе Била.

Научная новизна

Сформулированные в данной работе новые понятия и гипотеза предложены впервые.

Данная статья является продолжением работ [1] и [2], в которых вводились понятия абсолютной и фактической заполненности разрядов чисел. При этом в работе [1] давалось некоторое философское осмысление данных понятий. На примере двоичной системы счисления было показано, что чем больше заполненность разрядов того или иного числа, тем больше его мужественность. И соответственно чем меньше заполненность его разрядов, тем больше его женственность. Это справедливо не только для двоичной системы, но и для любой позиционной системы счисления.

Логическим продолжением данных работ является ввод понятия степени заполненности разрядов, а также понятия степени незаполненности разрядов, по аналогии с понятиями фактической заполненности и фактической незаполненности разрядов (см. работу [2]).

В философском понимании понятие степень заполненности разрядов представляет собой степень мужественности того или иного числа, а понятие степень незаполненности разрядов представляет собой степень женственности того или иного числа,

Итак, что же представляют собой данные понятия? Рассмотрим на примере десятичной системы счисления все трехзначные числа (3-ий уровень, или 3-я степень). Очевидно, среди всех этих чисел наименьшую заполненность разрядов будет иметь число 100, а наибольшую – число 999 (см. работу [2]). Значит степень незаполненности разрядов (степень женственности) числа 100 равна 3, а степень заполненности разрядов (степень мужественности) числа 999 также равна 3. По аналогии для четырехзначных чисел степень незаполненности разрядов числа 1000 равна 4, а степень заполненности разрядов числа 9999 также равна 4. И т.д.

Приведем теперь формулы для расчета степени заполненности и степени незаполненности разрядов для любого числа:

 

 

 

или

 

 

 

где S – основание той или иной системы счисления, натуральное число, S ≥ 2; СЗ – степень заполненности разрядов; СН – степень незаполненности разрядов; ФЗ% – процент фактической заполненности разрядов (минимальной); ФН% – процент фактической незаполненности разрядов (минимальной).

В работе [2] показано, что фактическая заполненность разрядов того или иного числа в той или иной системе счисления сводится к перевороту записи данного числа в данной системе счисления. Также в данной работе показано, как определяются фактическая незаполненность разрядов, а также проценты фактической заполненности и незаполненности разрядов.

Приведем пример. Десятичная система счисления. Число 123. Фактическая заполненность разрядов будет равна 321. Фактическая незаполненность разрядов будет равна 1000 – 321 = 679. Процент фактической заполненности разрядов будет равен 321 / 1000 ∙ 100% = 32.1%. Процент фактической незаполненности разрядов будет равен 679 / 1000 ∙ 100% = 67.9%. В данной работе акцентироваться внимание на данных понятиях не будет, так как о них подробно написано в работе [2].

Поскольку величины ФЗ% / 100% и ФН% / 100% находятся в интервале от 0 до 1, то величины СЗ и СН будут находиться в интервале от 0 до ∞. Например, число 0 имеет СЗ = 0 и СН = ∞ в любой системе счисления.

Из уравнений (1) и (2) вытекает следующая связь между степенью заполненности (СЗ) и степенью незаполненности (СН) разрядов того или иного числа:

 

 

 

Данное выражение можно преобразовать до следующего вида:

 

 

 

Если ввести следующие обозначения:

 

 

 

то уравнение (6) будет иметь следующий вид:

 

 

 

Уравнения такого вида изучались в работе [5].

Условную операцию получения значения того или иного числа «a» по его степени заполненности (СЗ) в той или иной системе счисления (S) будем обозначать так:

 

 

 

А условную операцию получения значения того или иного числа «a» по его степени незаполненности (СН) в той или иной системе счисления (S) будем обозначать так:

 

 

 

Если же та или иная формула справедлива и для степени заполненности, и для степени незаполненности, то такую операцию будем обозначать так:

 

 

 

где С – степень заполненности / незаполненности разрядов.

Исходя из вышесказанного, приведем в таблицах величины степени заполненности и степени незаполненности разрядов для систем счисления от двоичной и до десятичной:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

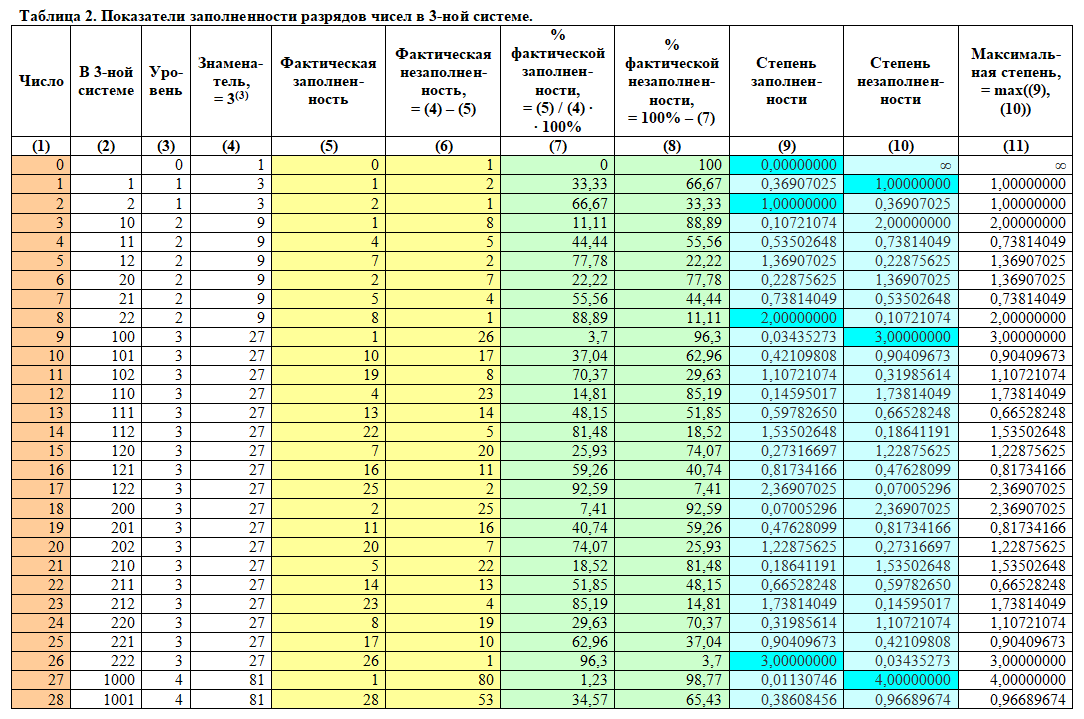
В данных таблицах ярко-голубым цветом выделены целочисленные значения степени заполненности и степени незаполненности разрядов. И нетрудно заметить следующую очевидную закономерность. Если определенное число «a» имеет целочисленное значение степени заполненности разрядов равное «n», то число «a + 1» будет иметь целочисленное значение степени незаполненности разрядов равное «n + 1». При этом для всех чисел для целочисленных степеней заполненности / незаполненности разрядов (n) будут справедливы следующие формулы:

 

 

где [n] – степень заполненности разрядов; {n} – степень незаполненности разрядов, см. формулы (10) и (11).

А для нецелочисленных степеней заполненности / незаполненности разрядов будут справедливы следующие неравенства:

 

 

 

Как уже понятно, если то или иное число в той или иной системе счисления «S + 1» имеет целочисленное значение степени заполненности разрядов, то его представление в этой системе счисления имеет такой вид:

 

 

 

А если то или иное число в той или иной системе счисления имеет целочисленное значение степени незаполненности разрядов, то его представление в этой системе счисления имеет такой вид:

 

 

 

Как видно из таблиц 1 – 9, любое число имеет хотя бы в одной системе счисления целочисленное значение степени заполненности разрядов и хотя бы в одной системе счисления целочисленное значение степени незаполненности разрядов. Для каждого числа можно определить максимальное целочисленное значение степени заполненности (МЦСЗ) и максимальное целочисленное значение степени незаполненности разрядов (МЦСН).

Для подавляющего большинства чисел будет справедлива следующая очевидная закономерность. То или иное число «a» будет иметь максимальную целочисленную степень заполненности разрядов равную 1 в системе счисления «a + 1». И то или иное число «a» будет иметь максимальную целочисленную степень незаполненности разрядов равную 2 в системе счисления «a».

Можно составить следующую таблицу максимальных целочисленных значений степени заполненности и степени незаполненности разрядов чисел:

 

 

 

Как видно из таблицы, выше написанное правило всегда выполняется: если то или иное число «a» имеет максимальное целочисленное значение степени заполненности равное «n», то число «a + 1» имеет максимальное целочисленное значение степени незаполненности равное «n + 1». Для наглядности данная закономерность в таблице 10 отмечена цветами.

Также из таблицы 10 видно, что любое число, начиная с 2, имеет МЦСЗ ≥ 1 и МЦСН ≥ 2. Исключением из этого правила являются только числа 0 и 1.

Числа 0 и 1.

Об уникальности чисел 0 и 1 говорилось в работе [1], приводилось также их философское осмысление. Как видно, понятие степени заполненности / незаполненности разрядов подтверждает уникальность этих чисел.

Число 0 является единственным числом, имеющим СЗ = 0 и СН = ∞ в любой системе счисления:

 

 

Число 1 является единственным числом, имеющим СН = 1 в любой системе счисления.

 

 

 

Великая теорема Ферма.

Из формулы (14) вытекает, что уравнение Великой теоремы Ферма можно записать в таком виде:

 

 

 

где a, b, c – взаимно простые натуральные числа ≥ 2; n – натуральное число > 3.

При преобразовании данного уравнения к привычному виду согласно формуле (14) оно будет выглядеть так:

 

 

 

При желании последнее уравнение можно записать и в классическом виде:

 

 

 

в котором будет n > 2.

Таким образом, Великую теорему Ферма можно записать, используя понятие степени незаполненности разрядов. Но есть еще зеркально противоположное понятие степени заполненности разрядов и формула (13).

Поэтому закономерно попробовать предложить теорему, имеющую более общий вид, чем Великая теорема Ферма.

Великая теорема Харта.

Правильнее назвать ее конечно гипотезой. Но поскольку она содержит в себе как бы «вторую сторону медали» Великой теоремы Ферма, которая в свою очередь также является не теоремой, а гипотезой (она стала теоремой Уайлса после того, как он ее доказал), поэтому и в данной работе предлагаемая гипотеза названа так, как названа.

В уравнении Великой теоремы Ферма имеются одинаковые степени «n» у всех трех членов уравнения. Обобщением этой теоремы на случай разных степеней у членов уравнения является гипотеза Била. Поэтому имеет смысл предложить формулировку новой теоремы сразу для произвольных степеней.

Формулировка. Для взаимно простых натуральных чисел a, b, c ≥ 2 и натуральных чисел x, y, z > 3 не существует решений уравнения:

 

 

 

Как понятно из вышесказанного, данная теорема разделяется на две части. Если в уравнении (25) стоят степени заполненности разрядов:

 

 

 

и если в уравнении (25) стоят степени незаполненности разрядов:

 

 

 

Уравнения (26) и (27) можно преобразовать по формулам (13) и (14) к виду:

 

 

 

В этих уравнениях x, y, z > 3. Естественно уравнение (29), если условиться, что x, y, z > 2, при желании можно записать и в классическом виде:

 

 

и при равных показателях x = y = z = n уравнение (30) – уравнение гипотезы Била – станет уравнением Великой теоремы Ферма:

 

 

Великую теорему Харта можно представить в следующем удобном виде:

 

Рис. 1. Великая теорема Харта.

 

Осмысление теоремы.

Уравнение гипотезы Била (в том числе и уравнение ее частного случая – Великой теоремы Ферма) – уравнение (27) – можно записать через представление чисел в той или иной системе счисления в таком виде:

 

 

Это только одна часть Великой теоремы Харта. Вторую ее часть – уравнение (26) – также можно записать через представление чисел в той или иной системе счисления:

 

 

где A = a – 1; B = b – 1; C = c – 1.

В работе [1] числа, имеющие представление в той или иной системе счисления 10, 100, 1000, 10000 и т.д., мы назвали настоящими женщинами. Они имеют минимальную заполненность разрядов на своем уровне. А числа, имеющие представление в той или иной системе счисления 99, 999, 9999, 99999 и т.д. (на примере десятичной системы счисления), мы назвали настоящими мужчинами. Они имеют максимальную заполненность разрядов на своем уровне.

Таким образом, первая часть Великой теоремы Харта – гипотеза Била и Великая теорема Ферма – это теорема королев:

 

 

А вторая часть Великой теоремы Харта это теорема королей:

 

 

Хартовы тройки чисел.

Если в уравнении (30) – первая часть теоремы – будут стоять одинаковые показатели степеней, то максимальная степень, при которой будут целочисленные решения этого уравнения, равна 2:

 

 

Натуральные числа a, b, c, удовлетворяющие этому уравнению, называются пифагоровыми тройками чисел. К ним относятся, например, тройки: (3, 4, 5); (5, 12, 13); (7, 24, 25) и т.д.

А если в уравнении (28) – вторая часть теоремы – будут стоять одинаковые показатели степеней, то максимальная степень, при которой будут целочисленные решения этого уравнения, равна 3:

 

 

Поскольку в данном уравнении содержатся только нечетные степени, для которых выполняется свойство -a³ = (-a)³, то данное уравнение может быть записано и так:

 

 

или

 

 

По аналогии с пифагоровыми тройками чисел такие тройки чисел, удовлетворяющие уравнениям (37) и (38), назовем хартовыми. Примеры таких троек чисел: (9, 10, 12); (64, 94, 103); (73, 144, 150) – для уравнения (37); (6, 8, 9); (71, 138, 144); (135, 138, 172) – для уравнения (38).

Имеются и примеры этих уравнений, где все три числа нечетные: (11767, 41167, 41485) – для уравнения (37); (1851, 8675, 8703) – для уравнения (38).

У данных троек чисел практически всегда наблюдается отсутствие попарной взаимной простоты. Но все три числа будут взаимно простыми.

Поскольку мы в уравнении (37) так легко поменяли знак у числа 1 на минус, получив уравнение (38), то может возникнуть вопрос: а можно ли точно так же поменять знак у числа 1 на минус в уравнении (28)?

Нет, нельзя. Поскольку в этом уравнении могут содержаться и четные показатели степеней. И как доказательство этому: решений уравнения (28) в целых числах при x, y, z > 3 нет, а при изменении знака числа 1 на минус решения будут. Например: 2⁴ + 2⁶ = 3⁴ – 1 и 14⁵ + 34⁴ = 37⁴ – 1.

Это лишь подтверждает корректность формулировки обеих частей Великой теоремы Харта – «женской» части и «мужской» части, сделанных на основе понятия заполненности разрядов чисел. Переходя к одинаковым показателям степеней в обеих частях теоремы, можно отметить, что «женская» теорема – Великая теорема Ферма:

 

 

где n > 2,

доказана.

А аналогичная «мужская» теорема:

 

где n > 3,

еще не доказана.

Выводы

1. Введены понятия степени заполненности и степени незаполненности разрядов чисел и показана их связь с понятиями фактической заполненности и незаполненности разрядов.

2. Приведены таблицы величин степени заполненности и степени незаполненности разрядов для систем счисления от двоичной и до десятичной для чисел от 0 и до 28.

3. Используя понятия степени заполненности и степени незаполненности разрядов, сформулирована Великая теорема Харта, частным случаем которой являются гипотеза Била и Великая теорема Ферма.

4. Дано определение понятия хартовых троек чисел и приведены их примеры.

1. Харт А. Философское осмысление чисел в контексте их женственности и мужественности [Электронный ресурс] // Электронный периодический научный журнал «SCI-ARTICLE.RU». 2021. №10. С. 16-27. URL: https://sci-article.ru/number/10_2021.pdf (дата обращения: 17.10.2023).
2. Харт А. Абсолютная и фактическая заполненность разрядов чисел [Электронный ресурс] // Электронный периодический научный журнал «SCI-ARTICLE.RU». 2021. №11. С. 54-76. URL: https://sci-article.ru/number/11_2021.pdf (дата обращения: 17.10.2023).
3. Харт А. Математическая игра «Империи» [Электронный ресурс] // SCI-ARTICLE.RU. 2022. URL: https://sci-article.ru/stat.php?i=1647640107 (дата обращения: 17.10.2023).
4. Харт А. Вариации игры «Короли» - частного случая математической игры «Империи» [Электронный ресурс] // SCI-ARTICLE.RU. 2023. URL: https://sci-article.ru/stat.php?i=1683190656 (дата обращения: 17.10.2023).
5. Мирмович Э. Г. МАТЕМАТИЧЕСКИЙ АДДИТИВНО-МУЛЬТИПЛИКАТИВНЫЙ ЭКВИВАЛЕНТ НА {Q} ТИПА А•В=А+В [Электронный ресурс] // Электронный периодический научный журнал «SCI-ARTICLE.RU». 2020. №12. С. 100-103. URL: https://sci-article.ru/number/12_2020.pdf (дата обращения: 17.10.2023).
6. Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с.
7. Гашков С.Б. Системы счисления и их применение. - М.: МЦНМО, 2004. - 52 с.

Комментарии пользователей:

7.01.2024, 13:22 Ремизов Вадим Григорьевич Отзыв: Уважаемый мистер Харт Алекс! Надо быть поскромнее и умерить свои математические амбиции. Несмотря на все Ваши потуги, Вам не подвинуть Пифагора. Я так и не понял, доказали ли Великую теорему Ферма и гипотезу Била, или не доказали.

7.01.2024, 18:42 Ремизов Вадим Григорьевич Отзыв: А, понял! Вы не доказали ни Великую теорему Ферма, ни гипотезу Била! Вы получили новые формулировки Великой теоремы Ферма и гипотезы Била с помощью гендерных чисел!

7.01.2024, 22:47 Харт Алекс Отзыв: Уважаемый Вадим Григорьевич! «Несмотря на все Ваши потуги, Вам не подвинуть Пифагора.» - Места на математическом олимпе хватит для каждого что-либо придумавшего или сделавшего полезное в математике человека. «Я так и не понял, доказали ли Великую теорему Ферма и гипотезу Била, или не доказали.» - Как видите у меня нет статей о доказательстве этих двух математических утверждений. В одной из статей Усова я писал сравнение доказательства теоремы Ферма для n=3 со здоровенным кабаном, которого он «победил» в одиночку голыми руками. Вы поверите, если кто-то будет утверждать, что победил здоровенного кабана в одиночку голыми руками? Вот Усов практически это и утверждает. А что утверждаете Вы? Вы утверждаете, что доказали теорему Ферма для всех n>2. Стало быть, Вы переплюнули Усова. Вы утверждаете, что победили не кабана, а здоровенного тигра голыми руками в одиночку. И Вы уже 30 лет так считаете, несмотря на все приведенные Вам доводы. Надо адекватно воспринимать противника. Вы поверите, что если кто-то скажет, что голыми руками победил здоровенного тигра в одиночку? Вы до сих пор не видите ошибки в своем доказательстве?

7.01.2024, 23:25 Харт Алекс Отзыв: "Вы получили новые формулировки Великой теоремы Ферма и гипотезы Била с помощью гендерных чисел!" - Никакого обобщения Вы в работе не увидели?

8.01.2024, 0:04 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Вашей фантазии и воображению можно только позавидовать, увидеть в целых числах детородные органы человека - это гениально. Вас не устраивают четные и нечетные числа, взамен Вы ввели женские и мужские числа. Можете успокоиться, Вы уже попали в книгу рекордов Гиннеса, разработав гендерную теорию чисел, за которую Вы несомненно заслуживаете премии шнобеля.

8.01.2024, 2:33 Харт Алекс Отзыв: "Вас не устраивают четные и нечетные числа, взамен Вы ввели женские и мужские числа" - Гениальный Вадим Григорьевич, а какое из двух чисел 2 и 6 более женственно если опираться только на понятие четного числа? Или надо вводить понятие более четное и менее четное число? "...Вы несомненно заслуживаете премии шнобеля" - Ну давайте. Еще чего-нибудь на подобие этому напишите. Аргументов у Вас естественно нет. На мои вопросы Вы ответить не в состоянии. Ну хоть немного поогрызайтесь в мой адрес. Так Вы еще более становитесь смешным. Так Вы до сих пор не видите ошибки в своем доказательстве?

10.01.2024, 14:46 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! У меня к Вам много вопросов, на которые я не могу ответить. Как Вы считаете, надо ли изучать Вашу гендерную теорию чисел в школе? И если да, то в каких классах ее надо изучать?

10.01.2024, 22:11 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Из Вашей гендерной теории чисел следует, что сумма двух мужских чисел равна женскому числу, а учитывая анатомическую аналогию, приходим, что два мужика равносильны одной женщине. Не кажется ли Вам, что Вы занимаетесь ЛГБТ пропагандой, которая в Российской Федерации запрещена Законом. Все это отвлекает учеников от изучения математики. Куда только смотрят модераторы и рецензенты.

10.01.2024, 22:25 Харт Алекс Отзыв: Я ввожу математическое понятие заполненности разрядов. А использоваться оно может по-разному. Например, в математической игре «Империи» оно используется в понимании силы и слабости той или иной империи. Более сильная империя может напасть на более слабую и присоединить к себе часть ее территории. Если Вы поиграете в эту игру например с помощью игральных карт, то Вы поймете насколько она красива, логична и интересна. И правила игры вполне может понять пятилетний ребенок. И там используется привычная десятичная система счисления. Можно также понятие заполненности разрядов использовать в понимании женственности и мужественности чисел. Здесь будет использоваться двоичная система счисления. И это уже близко к философии. Пифагорейцы тоже считали все четные числа женскими, а нечетные мужскими. Но они не определяли точную женственность и мужественность числа. Это можно сделать только с помощью понятия заполненности разрядов. Но в любом случае это уже ближе к философии. А философию в школе не изучают.

11.01.2024, 8:29 Харт Алекс Отзыв: Уважаемый Вячеслав Георгиевич! "Проверьте, пожалуйста следующее выражение для "мужской" половины Вашей Великой теоремы: 9^3 + 10^3 = 12^3 + 1" - Т.е. Вы статью просто посмотрели за 5 секунд одним глазом и готово опровержение? Я в отличие от Вас прежде чем публиковать сто раз проверяю. Итак. Видите такой текст в статье?: "Примеры таких троек чисел: (9, 10, 12)". Значит уже то, что Вы написали, мне известно. Числа 9, 10, 12 это одна из хартовых троек. Второе. Посмотрите рис. 1. Решений теоремы не должно быть при n>3 для "мужской" половины. И в чем проблема тогда?

11.01.2024, 8:35 Харт Алекс Отзыв: Уважаемый Вадим Григорьевич! "Не кажется ли Вам, что Вы занимаетесь..." - По Вашей логике, не кажется ли Вам, что пифагорейцы занимались указанной Вами пропагандой? По Вашей логике надо исключить Пифагора из школьной программы за такие дела? "Куда только смотрят модераторы и рецензенты" - Куда только смотрят в министерстве образования раз допустили Пифагора к изучению в школе. Так Вадим Григорьевич?

11.01.2024, 11:34 Харт Алекс Отзыв: "Но она на порядок сложнее, чем ВТФ" - Это и есть ловушка для непрофессионалов. Они думают: "О, лёгенькая теорема Ферма. Сейчас докажу ее за праздники." И впадают в просак, выглядев смешными в глазах окружающих. Они никогда не подумают, что 300 лет не могут найти простого решения великие математики мира для "лёгенькой" теоремы Ферма. Согласен, что "мужской" аналог еще сложнее. "Думаю, можно попробовать применить критикуемую Вами методику автора отзыва" - Когда Вы закончите редактировать свою статью и если к этому времени не поймете ее ошибочность, то видимо придется мне указать на ошибки в ней.

18.01.2024, 17:32 Харт Алекс Отзыв: Вячеслав Георгиевич, на рис. 1 полностью приведена конкретика.

18.01.2024, 23:59 Харт Алекс Отзыв: Уважаемый Вячеслав Георгиевич! Надеюсь когда-нибудь это будет!

Оставить комментарий