Разделы: Математика
Размещена 26.12.2023. Последняя правка: 31.03.2024.
Просмотров - 1094

ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА

Ремизов Вадим Григорьевич

Кандидат технических наук

Ярославский государственный технический университет

Доцент

Ремизов Константин Вадимович

УДК 510; 511; 517

Доказательство неразрешимости диофантовых уравнений в целых числах (доказательство Великой теоремы Ферма) основано на свойствах экстремумов непрерывных и гладких функций [1, 93 – 161 c, 197 – 222 c], у которых в точках экстремумов функции экстремумов являются непрерывными функциями. В точках, в которых функции экстремумов имеют разрывы, непрерывная и гладкая функция не может иметь экстремумы. Разрывы функций экстремумов в точках являются необходимыми условиями отсутствия экстремумов у непрерывных и гладких функций в указанных точках.

В отличие от методов теории чисел, используемых для решения диофантовых уравнений, при доказательстве теоремы Ферма парадоксально использован аппарат математического анализа непрерывных и гладких функций, который, как может показаться, не применим к задачам теории чисел. Для доказательства Великой теоремы Ферма (ВТФ) использован новый метод доказательства неразрешимости диофантовых уравнений в целых числах. При использовании нового метода задача нахождения целочисленных решений диофантова уравнения Ферма заменена эквивалентной задачей нахождения при  a = 1 нулевых локальных минимумов неотрицательной, периодической, непрерывной и гладкой функции.

В новом методе доказательства неразрешимости диофантовых уравнений в целых числах определены новые математические понятия - функции экстремумов в точках экстремумов и разрывы функций третьего рода в точках экстремумов.

Условия равенства нулю частных производных по независимым координатам  x и y называются необходимыми условиями существования экстремумов непрерывных и гладких функций. Необходимые условия существования экстремумов функций, содержащие четыре переменные  x, y, n, a, (если они удовлетворяются) представляют собой неявные уравнения, которые определяют неявные функции необходимых условий, содержащие четыре переменные  x, y, n, a. Если в этой неявной функции четырех переменных зафиксировать координаты точки экстремума x, y, то получим функцию экстремумов двух переменных  n, a  в точке экстремума с координатами  x, y,  то есть получим функцию переменной  n  в зависимости от переменной  a  в точке экстремума функции (2) с координатами  x, y.

Под непрерывными функциями понимаются функции, которые изменяются без мгновенных «скачков» (называемых разрывами), то есть такие функции, у которых малые изменения аргументов и параметров приводят к малым изменениям значений функции. Функция непрерывна в точке, если она определена в окрестности этой точки, и если существует предел функции при стремлении к этой точке и этот предел равен значению функции в этой точке. Непрерывные функции непрерывны во всех точках области определения функции. Другими словами непрерывная функция – это функция, которая изменяется непрерывно при изменении переменных и параметров.

Под гладкими функциями понимаются функции, имеющие непрерывные частные производные всех порядков на всем множестве их определения.

Функция непрерывна в точке, если она не имеет разрывов в указанной точке. Точкой разрыва функции называется точка, в которой функция не является непрерывной. Это означает, что в этой точке функция может иметь различные значения или не иметь значения вовсе. Точка разрыва функции – это значение аргумента, при котором функция не определена или ее значение не является конечным.

Известны два рода разрывов функции в точке. Точка неустранимого (конечного) разрыва первого рода. Если в точке существуют конечные пределы, то точка называется точкой разрыва первого рода. Существуют левый и правый пределы, но они различны (не равны). Функцию невозможно доопределить. Разность пределов называется скачком функции в точке разрыва. Точка устранимого разрыва первого рода. В точке значение функции не определено, но существуют левый и правый пределы, которые равны. Функцию можно доопределить в этой точке значением предела и сделать функцию непрерывной (устранить разрыв). Точкой разрыва второго рода называется точка, в которой функция не имеет, хотя бы, одного из односторонних пределов или хотя бы один из них бесконечен.

Другими словами, функция называется непрерывной в точке, если: 1) функция определена в точке; 2) существует конечный предел функции в точке; 3) этот предел равен значению функции в точке. Точка, в которой нарушено хотя бы одно из трех перечисленных условий непрерывности функций, называется точкой разрыва функции [1, 98 – 106 c.].

У непрерывных и гладких функций при изменении параметров положение экстремумов изменяется непрерывным образом. Обычно под прерывностью (разрывностью) функций понимается скачкообразное изменение значений функции в точке. Однако имеют место и разрывы функций третьего рода, под которыми понимается скачкообразное изменение положения экстремума, то есть скачкообразное изменение координат точек экстремумов, другими словами под разрывом функций третьего рода понимается исчезновение экстремума в точке экстремума. Такой разрыв для непрерывных и гладких функций не может иметь места. Такой разрыв может иметь место только, когда функции необходимых условий и функции экстремумов в точках экстремумов имеют разрывы. Поэтому у непрерывных и гладких функций в точках экстремумов функции необходимых условий и функции экстремумов непрерывны!

Непрерывные и гладкие функции не должны иметь разрывов первого и второго рода во всех точках области определения, а точках экстремумов и разрывов третьего рода.

Из определения непрерывной и гладкой функции следует непрерывность изменения координат точек экстремумов. Разрывность (не непрерывность) координат точек экстремумов эквивалентна разрывности третьего рода. У непрерывной и гладкой функции скачкообразное изменение положения экстремума функции или исчезновению экстремума в точке экстремума невозможно. Поэтому, для того, чтобы координаты точек экстремумов были непрерывными функциями необходимо и достаточно, чтобы функции необходимых условий и функции экстремумов в точках экстремумов функции были непрерывными!

При непрерывном изменении параметров непрерывной и гладкой функции, координаты точек локальных экстремумов  x, y  непрерывной и гладкой функции и значения самой функции изменяются непрерывным образом, то есть непрерывность координат точек экстремумов при непрерывном изменении параметров является следствием непрерывности самой непрерывной и гладкой функции. Скачкообразное изменение координат точек экстремумов непрерывной и гладкой функции приводит к исчезновению экстремума в точке экстремума, что равносильно разрывности третьего рода непрерывной и гладкой функции, что для непрерывной и гладкой функции невозможно.

Теорема Ферма утверждает, что диофантово уравнение Ферма (1) не имеет решений в целых ненулевых числах  x,  y,  z,  n при целом  n > 2 [2, 78 – 95 p.].

Будем натуральные числа x,  y,  z,  n, которые удовлетворяют диофантову уравнению Ферма (1), называть корнями диофантова уравнения Ферма.

Следует заметить, что

- если  n = 1, то нелинейное диофантово уравнение (1) вырождается в линейное диофантово уравнение z = x + y, которое имеет целочисленные решения при любых целых x и y;

- если  x = y, то диофантово нелинейное уравнение Ферма (1) с двумя независимыми переменными вырождается в линейное диофонтово уравнение  `root(n)(2)`  с одной независимой переменной, которое не имеет целочисленных решений. Поэтому целочисленные решения уравнения Ферма (1) будем искать во множестве различных целых  x и y;

- если  n = 2, то диофантово уравнение Ферма (1) разрешимо в целых числах, а его решениями являются Пифагоровы тройки.

- если  n > 2, то требуется доказать, что диофантово уравнение Ферма (1) не имеет целочисленных решений.

Для доказательства теоремы Ферма надо рассмотреть вещественную, неотрицательную, периодическую, непрерывную и гладкую функцию (2), соответствующую диофантову уравнению Ферма (1)

где зависимая переменная  z  определяется зависимостью

В функции (2)  x, y  `in` (0,+ oo) – положительные вещественные переменные, n `in` [1,+ oo ) – положительный вещественный параметр,  a – вещественный параметр с областью определения в точке  a = 1 и ее ближайшей окрестности, где n = n(a) > 0. Вещественные параметры  n  и  a  могут рассматриваться и как переменные.

Очевидно, что при  a = 1  только целые значения  x,  y,  z  и n  (корни диофантова уравнения Ферма) обращают функцию (2) в ноль и поэтому только корни диофантова уравнения Ферма (1) при  a = 1 доставляют вещественной, неотрицательной, периодической, непрерывной и гладкой функции (2) нулевые локальные минимумы. Справедливо и обратное  утверждение, что только  целые  значения переменных  x,  y, z  и n, которые  при  a = 1 доставляют функции (2) нулевые локальные минимумы, являются корнями диофантова уравнения Ферма (1). Задача нахождения целочисленных решений диафонтова уравнения Ферма (1) и задача определения при  a = 1 координат нулевых локальных минимумов неотрицательной, периодической, непрерывной и гладкой функции (2) являются эквивалентными, поскольку указанные задачи имеют одно и то же решение. Таким образом, установлена прямая связь между целочисленной математикой и математикой периодических, непрерывных и гладких функций!

Поэтому доказательство разрешимости диофантова уравнения Ферма (1) в целых числах сводится к доказательству наличия у периодической, непрерывной и гладкой функции (2) нулевых  локальных  минимумов  в  точках  с целыми  координатами  x, y  при целом  n >2  и a = 1, а доказательство неразрешимости диофантова уравнения Ферма (1) в целых числах сводится к доказательству отсутствия у периодической, непрерывной и гладкой функции (2) нулевых локальных минимумов в точках с целыми координатами  x, y  при целом  n > 2  и  a = 1.

Таким образом, для доказательства теоремы Ферма необходимо исследовать необходимые условия существования экстремумов вещественной, неотрицательной, периодической, непрерывной и гладкой функции (2).

Для неотрицательной, непрерывной и гладкой функции (2) в точках нулевых локальных минимумов необходимые условия существования экстремумов функции (2) являются и достаточными.

Запишем необходимые условия существования экстремумов функции (2) в произвольной точке с координатами  x и y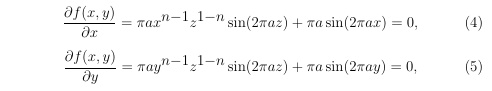

где  z  определяется зависимостью (3).

Из уравнений (4) и (5) с помощью эквивалентных преобразований можно исключить зависимую переменную  z  и получить еще одно необходимое условие существования экстремумов (6) непрерывной и гладкой функции (2)

Полученное необходимое условие существования экстремумов (6) содержит только независимые переменные  x  и  y, поэтому оно будет удовлетворяться при  a = 1 и любых различных целых  x  и  y, в то время как условия (4) и (5) при  a = 1 могут удовлетворяться только, когда при заданных целых  x,  y  и  n зависимая переменная  z  будет целой.

Таким образом, для определения координат точек экстремумов (нулевых локальных минимумов) функции (2) имеем любые два уравнения из трех уравнений (4), (5) и (6) с четырьмя неизвестными  x,  y,  n,  a.

Необходимые условия существования экстремумов (4), (5) и (6) функции (2) можно записать и в таком виде

Необходимые условия существования экстремумов функции (2) в точках экстремумов (условия равенства нулю производных по независимым переменным), если они удовлетворяются и содержат четыре неизвестные  x, y, n, a, являются неявными уравнениями, решениями которых являются явные и неявные функции, которые будем называть функциями необходимых условий. У непрерывной и гладкой функции (2) в точках экстремумов функции необходимых условий  являются непрерывными функциями.

В случае доказательства теоремы Ферма, уравнения (4), (5), (6) и функции необходимых условий содержат четыре неизвестные  x, y, n, a, которые можно рассматривать как четыре координаты точки экстремума функции (2) в гиперплоскости X0Y.  Из неявных уравнений можно в явном виде выразить одну неизвестную через оставшиеся три неизвестные (получить в явном виде функцию необходимых условий), например, параметр  n  записать как функцию трех переменных x, y, a,  и получить явную функцию  n = n (x,y,a). Здесь  n   является функцией трех аргументов  x, y, a. Полученную функцию необходимых условий  можно трактовать как множество функций  n = n(a)  в различных точках экстремумов функции (2) с координатами  x и y. Если зафиксировать координаты  x, y  точки экстремума функции (2), то получим функцию  n = n(a)  (зависимость параметра  n  от параметра  a)  в точке экстремума с фиксированными координатами  x  и  y. Функцию  n = n(a)  в точках экстремумов функции (2) с фиксированными координатами  x  и  y  будем называть функциями экстремумов в точках экстремумов. Для неявного уравнения (6) в точках экстремумов с целыми координатами  x0  и  y0  функция экстремумов может быть записана в виде (7). У непрерывной и гладкой функции (2) функции экстремумов в точках экстремумов не имеют разрывов и являются непрерывными функциями. Поэтому непрерывность функций экстремумов  в точке является необходимым условием существования экстремума у непрерывной и гладкой функции в указанной точке.

В точках, в которых функции экстремумов  имеют разрывы, непрерывная и гладкая функция не может иметь экстремумы. Поэтому наличие разрывов у функции экстремумов в точке является необходимым условием отсутствия экстремумов у непрерывных и гладких функций в указанной точке. Поэтому, чтобы ответить на вопрос может ли непрерывная и гладкая функция иметь экстремум в точке, необходимо исследовать на непрерывность  функцию экстремума  в указанной точке.

Таким образом, если в какой-либо точке  функция экстремума  является непрерывной функцией и не имеет разрывов, то непрерывная и гладкая функция (2) в этой точке может иметь экстремум (нулевой локальный минимум) - это необходимое условие существования экстремума у непрерывной и гладкой функции (2) в указанной точке. А если в какой либо точке  функция экстремума  имеет разрывы, то непрерывная и гладкая функция (2) в этой точке не может иметь экстремум (нулевой локальный минимум) – это необходимое условие отсутствия экстремума у непрерывной и гладкой функции (2) в указанной точке.

Наличие разрывов у  функций экстремумов  в точках с целыми координатами является необходимым условием отсутствия нулевых локальных минимумов у периодической, непрерывной и гладкой функции (2) в точках с целыми координатами  x0  и  y0.

Следует заметить, что случаи, когда при заданных целых  x,  y,  n  зависимая переменная  z является целой и не является целой, должны рассматриваться отдельно.

Алгоритм доказательства разрешимости (неразрешимости) в целых числах диофантовых уравнений состоит в следующем:

1. Задаться значением параметра n, проверяемым на неразрешимость диофантова уравнения, и значениями целых координат  x0 и y0  произвольной точки экстремума функции (2), и вычислить значение зависимой переменной  z  по формуле (3).
2. Если зависимая переменная  z  окажется целой, то получено целочисленное решение диофантова уравнения Ферма (1), то есть доказано, что диофантово уравнение Ферма (1) имеет целочисленные решения. В этом случае уравнения (4) и (5) удовлетворяются, функция (2) имеет нулевой локальный минимум, уравнение (6) не определяет функцию экстремума, поскольку уравнение (6) эквивалентно системе двух независимых уравнений  sin(2`pi` a x) = sin(2`pi` a y) = 0, которые не являются неявными уравнениями, определяющими  функции экстремумов, поскольку содержат менее четырех неизвестных, поэтому нет функций экстремумов, которые можно было бы  исследовать на непрерывность. Установлена разрешимость диофантова уравнения в целых числах, и что новый метод доказательства неразрешимости диофантовых уравнений в этом случае не может быть применен!
3. Если зависимая переменная z  окажется нецелой, то уравнения (4) и (5) не удовлетворяются, поэтому в точке с координатами  x0 и y0  функция (2) при  a=1  не будет иметь нулевого локального минимума. А вопрос о наличии нулевых локальных минимумов у функции (2) в других точках экстремумов с целыми координатами остается открытым. Для того, чтобы ответить на этот вопрос надо исследовать на непрерывность функции экстремумов в точках экстремумов функции (2)  с целыми координатами  x0 и y0  при  a=1, то есть применить новый метод доказательства неразрешимости диофантовых уравнений в целых числах. В этом случае, уравнение (6)  sin(2`pi` a x)/x^(n-1) = sin(2`pi` a y)/y^(n-1) <=>  0  будет являться неявным уравнением, которое будет определять функции экстремумов. Если функции экстремумов  n=n(a)  при  a=1  в точках экстремумов с целыми координатами  x0  и  y0  будут непрерывными, то функция (2) будет иметь в других точках нулевые локальные минимумы, то есть диофантово уравнение имеет целочисленные решения, а если функции экстремумов  n=n(a)  в точках экстремумов с целыми координатами  x0  и  y0  при  a=1 будут иметь разрывы, то функция (2) в других точках не будет иметь нулевые локальные минимумы, а диофантово уравнение не будет иметь целочисленные решения.

Сначала рассмотрим случай, когда при заданных целых  x,  y,  n  зависимая переменная  z  не является целой.

Когда диофантово уравнение Ферма (1) не имеет целочисленных решений, то при целых x,  y,  n  переменная  z  не будет целой, а поэтому при  a = 1  и целых  x,  y,  n  неявные уравнения (4) и (5) не будут удовлетворяться, и поэтому эти уравнения не определяют функции экстремумов, которые можно было бы исследовать на непрерывность.

Исследовать на непрерывность можно только функции экстремумов, которые определяются только неявным уравнением (6), которое удовлетворяется при любых целых  x, y, n  и  a=1. Необходимое условие существования экстремумов (6) функции (2) является неявным уравнением, решением которого является  функция экстремумов (7)  n = n(a)  в точках экстремумов с фиксированными целыми координатами  x0  и  y0.

Выразим из неявного уравнения (6)  функцию экстремума  (7)  n = n(a)  в произвольной точке экстремума с целыми фиксированными координатами  x0  и  y0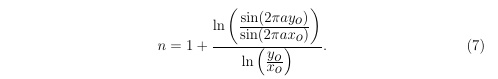

На Figure 1 и FIgure 2 показаны  функции экстремумов  n = n(a)  и график минимумов функции (2) f(min) в окрестности точки  a = 1.

Figure 1. Функции экстремумов  n(a)  при фиксированных  x0  и  y0.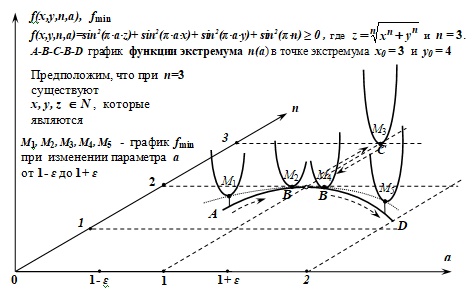

FIgure 2. Функция экстремумов n = n(a)  (A-B-C-B-D) при фиксированных  x0 = 3  и  y0 = 4  и график минимума функции (2)  fmin   (M_1-M_2-M_3-M_4-M_5) в зависимости от значений параметра  a  окрестности точки  a = 1.

Функция экстремумов (7) в точке  a = 1  неопределенна, в числителе дроби имеет место неопределенность типа 0/0. Чтобы  функция экстремумов  (7)  n = n(a)  была эквивалентна (соответствовала) непрерывной и гладкой функции (2) и диофантову уравнению Ферма (1), ее в точке  a = 1  надо доопределить значением  n, равным значению  n  в диофантовом уравнении Ферма (1) и в непрерывной и гладкой функции (2).

Исследуем на непрерывность  функцию экстремума (7) n = n(a)  в произвольной точке экстремума функции (2) с различными фиксированными целыми координатами  x0  и  y0  при  a = 1.

Для того, чтобы установить, является ли  функция экстремумов (7)  n = n(a)  непрерывной в точке  a = 1, надо установить предел, к которому стремится  функция экстремумов (7) n = n(a)  при стремлении  a  1. Вычислим этот предел по правилу Лопиталя.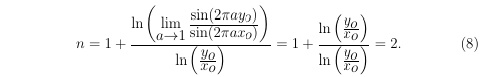

Из уравнения (8) следует, что при различных целых координатах точек экстремумов  x_o  и  y_o  функции (2) уравнение (8) имеет единственное решение  n = 2.

Установим целые значения параметра  n, при которых  функция экстремумов (7) n = n(a)  при  a = 1 в произвольной фиксированной точке экстремума с целыми координатами  x0  и  y0  будет иметь разрыв, а непрерывная и гладкая функция (2) в указанной точке при  a = 1  не будет иметь нулевого локального минимума.

Если в диофантовом уравнении Ферма (1) и в  функции экстремумов (7) при  a = 1 значение  n = 2, то функция экстремумов (7)  n = n(a)  будет непрерывной, а если в диофантовом уравнении Ферма (1) и в  функции экстремумов (7) при  a = 1 значение  n > 2, то  функция экстремумов (7)  n = n(a)  будет иметь разрыв в точке  a = 1.

Поскольку мы рассматривали условия непрерывности  функции экстремумов (7)  n=n(a) в произвольной точке экстремума с целыми, различными координатами  x0  и  y0, то полученные выводы будут справедливы при  a = 1  для всех точек экстремумов функции (2) с целыми различными координатами  x0  и  y0. Откуда следует, что непрерывная и гладкая функция (2) при целом  n > 2  и  a = 1  не будет иметь нулевых локальных минимумов, а диофантово уравнение Ферма (1) не будет иметь целочисленных решений при  n > 2. Функция (2) может иметь нулевые локальные минимумы при  a = 1 и диофантово уравнение Ферма (1) целочисленные решения только при значении  n = 2.

Полученный вывод не находятся в противоречии с тем, что диофантово уравнение Ферма (1) имеет решения и при   n = 1, поскольку указанный вывод был получен для случая, когда зависимая переменная  z  была нецелой. Чтобы разобраться в этом вопросе, надо рассмотреть случай, когда зависимая переменная  z  является целой. И так, зависимая переменная  z  является целой.

В этом случае необходимые условия существования экстремумов (4) и (5) удовлетворяются, что свидетельствует о том, что функция (2) при  a = 1,  n = 1 и целых  x, y, z  имеет нулевой локальный минимум, а диофантово уравнение Ферма (1) имеет целочисленные решения. Так в чем проблема? А проблема в том, что в этом случае решение системы уравнений (4), (5) и (6) эквивалентно системе трех независимых уравнений (9), которые не являются неявными уравнениями, поскольку содержат менее четырех неизвестных, и которые не определяют функции экстремумов, которые могли бы исследоваться на непрерывность!

В  этом  случае  уравнение  (6)  эквивалентно  системе  двух  независимых  уравнений sin(2 a x)= sin(2 a y)=0,которые не являются неявными уравнениями (поскольку содержат менее четырех неизвестных), определяющими неявные функции в точках экстремумов.  Поэтому уравнение (6) не является неявным уравнением, которое бы определяло  функцию экстремумов, которую можно было бы исследовать на непрерывность в точках экстремумов.

Таким образом, показали, что при  n = 1, когда зависимая переменная  z  является целой, при любых целых  x, y, невозможно определение   функций экстремумов  n = n(a)  для их исследования на непрерывность в точках экстремумов, и поэтому новый метод доказательства неразрешимости диофантовых уравнений не применим.

Следует подчеркнуть, что новый метод доказательства неразрешимости диофантовых уравнений в целых числах применим только в случаях, когда зависимая переменная  z  не является целой, и не применим, когда зависимая переменная  z  является целой.

ТАКИМ ОБРАЗОМ, ТЕОРЕМА ФЕРМА ДОКАЗАНА. И доказана с помощью математического анализа экстремумов периодических, непрерывных и гладких функций.

Теперь рассмотрим примеры применения нового метода доказательства неразрешимости диофантовых уравнений в целых числах в некоторых частных случаях, для чего надо задаться целыми координатами экстремума  x_o  и  y_o  и проверяемым значением параметра  n  и вычислить значение зависимой переменной  z. Новый метод доказательства неразрешимости диофантовых уравнений может применяться, если зависимая переменная  z  является нецелой, и не может применяться, когда зависимая переменная  z  является целой, потому что в этом случае нельзя получить  функции экстремумов, которые следует исследовать в точках экстремумов на непрерывность.

Случай I, когда  n = 2,  x = 3,  y = 4. В этом случае  z = `sqrt(3^2+4^2)`  = 5 - целое. В этом случае необходимые условия существования экстремумов (4) и (5) удовлетворяются, функция (2) в этой точке при  a = 1  имеет нулевой локальный минимум, а  n = 2,  x = 3,  y = 4,  z = 5  -  целочисленное  решение  диофантова  уравнения  Ферма.  Уравнение  (6) sin(2`pi` a x)= sin(2`pi` a y)=0  не является неявным уравнением и не определяет функции экстремумов, поэтому новый метод решения диофантовых уравнений не применим!

Случай II, когда  n = 2,  x = 3,  y = 5. В этом случае  z = `sqrt(3^2+5^2)`  = 5,83 - нецелое. В этом случае необходимые условия существования экстремумов (4) и (5) не удовлетворяются! В этой точке функция (2) при  a = 1  не имеет нулевого локального минимума. Вопрос о существовании целочисленных решений у функции (2) в других точках экстремумов при  a = 1  и  n = 2   остается открытым. Для его решения надо исследовать на непрерывность в точке экстремума  функцию экстремумов (7) n=n(a), определяемую неявным уравнением (6)  y^(n-1) sin(2 `pi` a x) =  x^(n-1) sin(2`pi` a y).  В этом случае заданное значение  n = 2  совпадает с пределом  функции экстремумов (8), поэтому функция экстремумов  в точке  a = 1  непрерывна, и поэтому при  a = 1  функция (2) при  n = 2  может иметь нулевые локальные минимумы, а диофантово уравнение Ферма (1) целочисленные решения!

Случай III, когда  n = 3,  x = 3,  y = 4. В этом случае  z = `sqrt(3^3+4^3)`  = 4,5 - нецелое. В этом случае необходимые условия существования экстремумов (4) и (5) не удовлетворяются! В этой точке функция (2) при  a = 1  не имеет нулевого локального минимума. Вопрос о существовании нулевых локальных минимумов у функции (2) в других точках экстремумов при  a = 1  и  n = 3  остается открытым.  Для его решения надо исследовать на непрерывность в точке экстремума  функцию экстремумов (7) n=n(a), определяемую неявным уравнением (6)  y^(n-1) sin(2`pi` a x) =  x^(n-1) sin(2 `pi` a y).  В этом случае заданное значение  n = 3  не совпадает с пределом функции экстремумов (8), равным  n = 2, поэтому  функция экстремумов в точке  a = 1 имеет разрыв, и поэтому при  a = 1  функция (2) при  n = 3  не может иметь нулевых локальных минимумов, а диофантово уравнение Ферма (1) целочисленные решения!

Контрпример. Этот контрпример мои оппоненты приводят для доказательства ошибочности нашего доказательства Великой теоремы Ферма. Они утверждают, что диофантово уравнение  z = x^n + y^n, очевидно, имеет целочисленные решения при любых целых  x,  y  и  n. А использование нового метода доказательства неразрешимости диофантовых уравнений дает противоположный результат, что это диофантово уравнение не имеет целочисленных решений при целых  n > 2. Ответ простой – при любых целых  x,  y  и  n  переменная  z  целая, поэтому условия (4) и (5) удовлетворяются, и поэтому диофантово уравнение имеет целочисленные решения, в то время как новый метод решения диофантовых уравнений при целом  z  не применим, как и в случае доказательства Великой теоремы Ферма при  n = 1.  В этом случае невозможно получить функцию экстремумов,которую можно было бы исследовать в точках экстремумов на непрерывность. Поэтому ни какого противоречия нет.

Доказательство Великой теоремы Ферма нами изложено в работах [3,4].

1. Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. М., Наука, 1974. - 832 с.
2. Эдвардс Г. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел. – М:, Мир, 1980. – 486 с.
3. Ремизов В.Г., Ремизов К.В. Доказательство теоремы Ферма. Ярославская областная ежедневная газета «Северный край», Ярославль, 2 ноября 1994 г., среда, № 189 (21819). – 4 с.
4. Ремизов В.Г., Ремизов К.В. Элементарное доказательство последней теоремы Ферма. XXIV Международная научная конференция Евразийского Научного Объединения (февраль 2017). Современные концепции научных исследований // Сборник научных работ XXIV Международной научной конференции Евразийского Научного Объединения (г. Москва, февраль 2017). — Москва: ЕНО, 2017. — 192 с.

Комментарии пользователей:

26.12.2023, 10:45 Харт Алекс Отзыв: Так, так, так. Кого я вижу! И конечно же Вы опять ошиблись. И Вы, и Усов, конечно же не доказали Великую теорему Ферма. Увы.

9.01.2024, 18:45 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Вы не понимаете различия между делением на ноль и нахождением предела функции при раскрытии по правилу Лопиталя неопределенностей типа 0/0. Я переписал неявную функцию в явном виде, а Вы заявляете, что я делю на нуль!

10.01.2024, 14:43 Харт Алекс Отзыв: "И доказана с помощью математического анализа экстремумов периодических, непрерывных и гладких функций" - Уважаемый Вадим Григорьевич! Неужели Вы считаете, что за 300 лет математики не пытались доказать теорему Ферма применяя в том числе и мат. анализ? Никто не пытался, а Вы перехитрили всех математиков и попытались и все получилось?

10.01.2024, 15:57 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Да, я не видел ни одной научной работы, в которой диофантовы уравнения решались бы с помощью непрерывных и гладких функций и была бы установлена связь целочисленной математики и математики непрерывных и гладких функций. Оказывается вашей буйной фантазии хватило только на детородные органы человека. Очевидно, что Вам не хватает математической грамотежки, поэтому Вы и не понимаете, что такое необходимые условия существования экстремумов функций, и в чем заключается новый метод решения диофантовых уравнений в целых числах. Чтобы основываться не на домыслах, а на фактах советую Вам все же прочитать нашу статью.

11.01.2024, 10:55 Харт Алекс Отзыв: «Да, я не видел ни одной научной работы, в которой диофантовы уравнения решались бы с помощью непрерывных и гладких функций и была бы установлена связь целочисленной математики и математики непрерывных и гладких функций.» - Может потому что это не дает никаких результатов? «Чтобы основываться не на домыслах, а на фактах советую Вам все же прочитать нашу статью» - Что изменилось в этой статье по сравнению с предыдущей? Предыдущую статью Вы по какой причине удалили?

11.01.2024, 17:41 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Меня поражает лень, злобность и невежество современных российских «псевдо математиков». Основными доказательствами, которыми они доказывают ошибочность нашего доказательства Великой теоремы Ферма, являются - 300 лет лучшие математики мира не могли доказать теорему Ферма, а поэтому и вы не можете доказать теорему Ферма. А почему Вы так думаете, пожалуйста объясните. Вы даже не собираетесь читать нашу статью, потому что этого не может быть никогда! И, конечно же, мы опять ошибаемся. Поэтому не надо бла, бла и еще раз бла. Укажите, где в нашем доказательстве Великой теоремы Ферма ошибка, иначе закройте свой РОТ. Вы, спрашиваете, почему я удалял предыдущие статьи, и что изменилось в этой статье? Да практически ничего не изменилось, суть доказательства осталась прежней, только доказательство ВТФ излагались на одной странице, на двух страницах и большем числе страниц и с большим количеством примеров и обоснований. Но, Вы, даже не пытались понять суть нашего метода доказательства ВТФ, а лихорадочно искали ошибки, которых не могли найти. Мы доказали ВТФ раньше англичанина Эндрю Уайлса и доказательство было изложено на одной странице, и доказательство было понятно школьникам, потому, что мне позвонила школьница и сказала, что мы доказали ВТФ, а доморощенные математики побоялись признать это. А удалял я статьи потому, чтобы Вы в них не запутались, то есть каждый раз писал статью с чистого листа. Вызывают у меня сомнения в компетентности рецензентов в разделе «математика». Они с умилением рекомендуют к публикации Ваши сексуальные фантазии, а о нашем доказательстве ВТФ не могут сказать ни слова, не могут сказать верное оно, или ошибочное. Они думают, что промолчат - за умных сойдут. Не выйдет, их молчание характеризует только их некомпетентность.

12.01.2024, 0:39 Харт Алекс Отзыв: Уважаемый Вадим Григорьевич! Вы только не кипятитесь. В это время года очень много нервных срывов. Берегите нервы. «300 лет лучшие математики мира не могли доказать теорему Ферма, а поэтому и вы не можете доказать теорему Ферма» - Я же Вам привел пример, который Вы благополучно продинамили. Я сравнил доказательство теоремы Ферма с победой над здоровенным тигром голыми руками. Теоретически это возможно. И какой-нибудь спортивный чемпион мира возможно и мог бы это сделать. Но какова вероятность, что это сделал обычный человек? Она очень и очень мала. Например 0.000001%. Ну вот и такая вероятность, что Вы в статье доказали теорему Ферма. А поскольку я уже знаком с Вашим доказательством по прошлым статьям, то вероятность того что Вы доказали в этой статье теорему Ферма равна 0%. «Вы даже не собираетесь читать нашу статью, потому что этого не может быть никогда!» - Ну прочитал я еще раз Вашу статью сейчас. Ну не смешите меня. Ну та же ошибка. «…потому, что мне позвонила школьница и сказала, что мы доказали ВТФ» - Блестяще. Мнение школьницы конечно же имеет огромный авторитет. Она уже наверно не школьница. Дайте мне ее контакт и я ей объясню Вашу ошибку, а она потом Вам перезвонит и скажет что Вы ошиблись в доказательстве. «доморощенные математики побоялись признать это» - Может не хотели Вас – доцента – расстраивать? А Вы согласны повысить ставки? Будет заключен договор. Настоящие математики, доктора наук, проверят Вашу работу. Если ошибок найдено не будет, то Вам автоматически присваивается степень доктора наук и возможно дадут еще награды. А если ошибка будет найдена, то Вы лишаетесь степени кандидата наук и звания доцента? Потому что такие ошибки не достойны этих регалий. Согласны? «Вызывают у меня сомнения в компетентности рецензентов в разделе «математика»» - Я думаю, что рецензенты молчат, потому что не хотят Вас расстраивать. Вы пенсионер, если я верно понял. Зачем Вас расстраивать. Ладно. Вернемся к ошибке в доказательстве. Во-первых можно легко доказать, что сам Ваш метод ошибочен просто применив его не к теореме Ферма, а к уравнению x^n+y^n+2=z^n. Я про это уже писал. Вы вынуждаете меня повторяться. Окажется, что оно не имеет решений по Вашей логике при n>2. Тогда как оно имеет решения в целых числах при n=3. Во-вторых. Где же ошибка в Вашем методе. Про это Вам уже писали. Переход от (6) к (7) это не эквивалентное преобразование. Из (6) видно, что если a=1, x и y – целые, то уравнение (6) превращается в уравнение 0=0 при любом n. Вы сами подумайте. Вы забудьте про теорему Ферма. У Вас есть уравнение (6). Точка. Не важно как Вы его вывели. Из теоремы Ферма или нет. Не важно. Точка. Оно имеет решение при всех целых x,y и a=1. Вне зависимости от n. Точка. А Вы из анализа (7) утверждаете, что это возможно только для n=2. Уже несостыковка. Вы можете сколько угодно исследовать график функции (7) на разрывы. Это никак не влияет на то, что уравнение (6) имеет решение при всех целых x,y и a=1. В-третьих. Вы очень аккуратно «обошли» случай n=1. Не удастся. Вы написали: «…имеет решения и при n=1, поскольку нелинейная функция (2) вырождается в линейное диофантово уравнение z=x+y, в котором отсутствует параметр n…». Простите, а при n=3 мы получим z^3=x^3+y^3. Здесь тоже отсутствует параметр n. Это тоже «делает невозможным определение функций экстремумов n=n(a)». Так что не удастся убрать случай n=1. Вот Вам три опровержения. Их Вам писали и раньше. Ваше доказательство неверно. Точка. Так что Вы уложились в оценочную вероятность 0.000001%, что неудивительно. Одно меня беспокоит. Что сколько угодно Вам не указывай на Ваши ошибки. Вы все равно будете писать: «Ну где? Где? Где моя ошибка?» Понимаю. Вы определили предел в (8) и получили n=2 и у Вас затряслись руки. Потому что у всех ферматистов просто бзик на n и 2. А что означает этот предел n=2? Только то, что если x,y целые и a стремится к 1, то уравнение (6) можно преобразовать к уравнению x^(n-2)=y^(n-2). И это уравнение будет всегда верно при n=2. Это к теореме Ферма отношения не имеет.

12.01.2024, 13:02 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Вы ведете себя как базарная баба. На каждом углу кричите, что «300 лет лучшие математики мира не могли доказать теорему Ферма, а поэтому и вы не можете доказать теорему Ферма». Приводите какие то неуместные сравнения с кабанами и тиграми. Оперируете с какими то вероятностями. Вы, что пытаетесь запугать меня Вашей эрудицией? Не запугаете! Вы не умеете вести научную дискуссию. Вы вывали на обеденный стол кучу го*на и заявляете - разбирайте это и найдете доказательства ошибочности своего доказательства ВТФ. Вы думаете, что чем больше куча дерма, тем больше в ней доказательств ошибочности доказательства ВТФ. Вы меня этой кучей навоза с ног не собьете. Вам ли не знать, что проверка доказательств производится с проверки истинности всех утверждений. И так начнем. Утверждение № 1. Ранее Вы утверждали, что ошибка в нашем доказательстве ВТФ состоит в том, что мы производим деление на ноль. Вы продолжаете это утверждать?

12.01.2024, 13:55 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Я согласен повысить ставки, только вот непонятно с кем заключать договор, с Вами? А Вы, что президент РАН, чтобы выдавать такие векселя. Вы обычный демагог. Вот уже 30 лет я пытаюсь направить наше доказательство на рецензирование, только вот не находится ни одного кандидата наук, не говоря уже о докторах наук, которые бы согласились рецензировать нашу статью. Все рассуждают, как и Вы, если 300 лет не могли доказать ВТФ, то и Я не могу доказать. А что касается степени кандидата наук и доцента, то их с собою не возьмешь на тот свет. Вы даже не допускаете, что я могу быть прав, это говорит о том, что Вы немой, глухой и слепой «ученый».

12.01.2024, 16:24 Харт Алекс Отзыв: Уважаемый Вадим Григорьевич! Ну не кипятитесь. Я Вам привел три опровержения. Вам мало? Разве что Архипову Вячеславу Георгиевичу еще не понятно, что Ваше доказательство ложно. Уважаемые читатели! Кто после приведенных мною доводов 12.01.2024, 0:39 еще считает верным доказательство Ремизова в данной статье? Напишите пожалуйста.

12.01.2024, 17:53 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Ну, что Вы все в одну кучу дерьма свалили. Дойдем и до Ваших трех опровержениях. Они ни куда не денутся. Но прежде прокомментируйте Утверждение № 1. Никогда не задавайте более одного вопроса (одного утверждения) и впредь давайте будем нумеровать вопросы и утверждения.

12.01.2024, 23:19 Харт Алекс Отзыв: Видимо господин Архипов Вячеслав Георгиевич думал, что его погладят по головке, когда он утверждал: "Я доказал теорему Ферма тем же методом, что и сам Ферма, у которого доказательство не влезло на полях книги".

12.01.2024, 23:27 Харт Алекс Отзыв: Уважаемый Ремизов Вадим Григорьевич! Я не планирую вести бесконечную дискуссию на подобие Вашей предыдущей статьи. Давайте к делу раз три моих очевидных опровержения для Вас мало что значат. Утверждение № 0. Уравнение (6) (и уравнение (4) и уравнение (5)) является необходимым условием существования экстремумов функции (2). И это верное утверждение. Рассуждайте дальше. Утверждение № 1. Напишите его.

13.01.2024, 13:43 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Я говорил Вам, не валите все в одну кучу, дойдем и до Ваших трех «очевидных опровержения» (вот уже пошли не только доказанные, но и очевидные опровержения). Чего Вы заистерили, не будите вести бесконечную дискуссию, да и не надо, с Вами все ясно!. Я понимаю, что Вам не хватает аргументов для ведения научной дискуссии, поэтому Вам хочется использовать любимое, для таких как Вы, псевдоматематиков, доказательство – провести опрос среди читателей и, если, не по квалифицированному большинству, то, по крайней мере, по простому большинству установить верное или неверное наше доказательство ВТФ. Вы все время пытаетесь пролезь без очереди, начали отсчет утверждений в отрицательном направлении и без очереди заявили Утверждение № 0 – «Уравнение (6) (и уравнение (4) и уравнение (5)) является необходимым условием существования экстремумов функции (2). И это верное утверждение». Не знаю чего Вы хотите доказать этим утверждением. Да, это утверждение верное! Ну, и что из этого. На каком основании Вы лишаете меня слова? Все? Теперь моя очередь. Во второй раз формулирую Утверждение № 1 – «Ранее Вы утверждали, что ошибка в нашем доказательстве ВТФ состоит в том, что мы производим деление на ноль. Вы продолжаете это утверждать?» Предупреждаю, что не буду отвечать сразу на три Ваших ОЧЕВИДНЫХ опровержения, только по одному опровержению! Но сначала мы должны разобраться с утверждением № 1.

13.01.2024, 22:59 Харт Алекс Отзыв: Да, ошибку в доказательстве можно назвать упрощенно «деление на 0». А теперь как человека математически плохо видящего я поведу рядом с собой на коротком поводке по мало понимаемой для Вас математической стране. Уравнение (6) разрешимо в целых числах при a=1. Если x,y целые, то для ЛЮБОГО «n» уравнение (6) выполняется. УЖЕ нельзя значит таким методом доказать теорему Ферма. Очень быстро отвечайте мне, на каком основании Вы от (6) переходите к (7)? При целых x,y и a=1 уравнение (6) чувствует себя отлично. А у уравнения (7) проблемы – деление на 0. Значит уже Вы не имели права делать такое преобразование. И я НЕ собираюсь с Вами нянчиться как с математическим малышом, достаточно капризным. Даю Вам домашнее задание. Полностью разобраться за неделю в условиях корректного перехода от (6) к (7). Какие ограничения при этом возникают. Если из (6) видно, что проблем нет при целых x,y и a=1, а у (7) проблемы, то из-за чего так произошло. Сформулируйте это математически правильно. Разберитесь. Если сами не можете, то привлеките на помощь соавтора Ремизова Константина Вадимовича. Неделя.

13.01.2024, 23:01 Харт Алекс Отзыв: Ремизов Константин Вадимович, Вы считаете приведенное в данной статье доказательство верным?

14.01.2024, 11:26 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Если Вы публично не признаете свои ошибки, то я прекращаю с Вами всякое общение. Вы должны публично заявить, что в нашем доказательстве ВТФ нет ошибки - деление на ноль.

14.01.2024, 14:06 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Я еще раз объясняю Вам, чего Вы не знаете и не понимает. "9.01.2024, 18:45 Ремизов Вадим Григорьевич Отзыв: Мистер Алекс Харт! Вы не понимаете различия между делением на ноль и нахождением предела функции при раскрытии по правилу Лопиталя неопределенностей типа 0/0. Я переписал неявную функцию (6) в явном виде (7), а Вы заявляете, что я делю на нуль!". Так, пожалуйста, скажите, чему равен результат от деления на ноль, и укажите где в статье это написано. Здесь Вам, не тут, здесь математика, а не химия. Не знаю какой Вы специалист по химии, то по математике - никакой, у Вас каша в голове и огромный апломб.

18.01.2024, 19:42 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Давайте подведем некоторые итоги нашей «научной дискуссии». 1. У вас главное доказательство ошибочности нашего доказательства ВТФ – «Этого не может быть, потому что не может быть никогда». 2. Раскрытие неопределенностей типа 0/0 по правилу Лопиталя не является делением на ноль. 3. В нашем доказательстве нет результатов деления на ноль, а раз нет результатов деления, то нет и самого деления на ноль. 4. Для доказательства того, что в нашем доказательстве Великой теоремы Ферма имеется ошибка – деление на ноль, Вы используете неопределенные в математике понятия – «Ошибку в доказательстве можно назвать упрощенно «деление на 0». Как это понимать? Непонятно! Я не понимаю, почему Вы не признаете, что допустили ошибку с «делением на ноль». У вас есть еще целых три «очевидные опровержения» верности нашего доказательства ВТФ. Так, что обязательно прокомментируйте утверждение № 1, это Вас ни к чему не обязывает.

21.01.2024, 0:25 Харт Алекс Отзыв: Неделя прошла. И что я вижу. Было дано задание: «Полностью разобраться за неделю в условиях корректного перехода от (6) к (7)». И это так Вы разобрались? Хуже первоклассника? Впрочем, о чем это я. Вы ведь 30 лет не можете найти простую ошибку. Понимаю. Ее выгодно не находить. Так Вы пользуетесь среди малопонимающих в математике людей огромными дивидендами от своего «доказательства» как человек гениальный, обошедший Уайлса. Это же так выгодно. Да еще и сделать своего сына вторым гением. А если найти ошибку, то ни Вы, ни сын гениями не являются. А являются обычными опростоволосившимися людьми, 30 лет не понимающими своей ошибки. И если где-то и есть доска позора, то на нее смело можно вписать еще двух сами понимаете каких людей. Вам просто нельзя искать ошибки в своем «доказательстве». Представьте, Вы ее найдете. И скажете об этом своим родственникам. Каково будет жене Вашего сына узнать, что она вышла замуж не за гения, а за обычного опростоволосившегося человека, который 30 лет считал себя гением? Поэтому Вам и нельзя искать свою ошибку. Стойте на своем. Все отрицайте. Ничего не было. Никаких ошибок. Итак. Начнем процедуру. До уравнения (6) ошибок в статье нет. Ошибка появляется уже, когда Вы бесцеремонно называете уравнение (6) неявной функцией. Пример для особо одаренных: имеем уравнение y^2=x. Нужно решить его в целых числах не превышающих 5. Решения: 1) x=0, y=0; 2) x=1, y=1; 3) x=1, y=-1; 4) x=4, y=2; 5) x=4, y=-2. Всего 5 решений. И тут приходит Ремизов и говорит: «Я хочу неявную функцию y(x) выразить явно». И делает такое движение, получая функцию y=Sqrt(x). И продолжает решать полученный результат в целых числах. И получает такие решения: ) x=0, y=0; 2) x=1, y=1; 3) x=4, y=2. Итого 3 решения. Гениально, Ремизов. Блестяще. В чем была ошибка? В первоначальном уравнении могли быть такие решения: x=1, y=1 и x=1, y=-1. Т.е. для одного x было два y. А если назвать это функцией y(x), то функция должна иметь для одного x только один y. Теперь вернемся к УРАВНЕНИЮ (6) в статье. В этом уравнении есть такие решения в целых числах при a=1: 1) n=1, x=1, y=1; 2) n=2, x=1, y=1; 3) n=3, x=1, y=1; 4) n=4, x=1, y=1 и т.д. (до бесконечности). Т.е. «a, x, y» одинаковые, а n – разные. Это все решения уравнения (6). Что делает Ремизов. Он говорит это теперь ФУНКЦИЯ n(a). И он еще под дурачка делает вместо x – x0, вместо y – y0. Но это дела не меняет. Но при заданных «a, x, y» было бесконечное количество решений, которые отличались только «n». Как же должна себя вести функция n(a) теперь? Она ведь может иметь максимум одно значение вместо бесконечного количества. В итоге оказывается, что она вообще не определена при a=1 и целых x,y. Это неудивительно. Даю более конкретное задание на следующую неделю. Разобраться. Нормально разобраться. А не как малолетний пацан, ничего не понимающий в математике. На каком основании Вы назвали уравнение (6), которое легко разрешимо в целых числах для любого «n», неявной функцией? Вы как будто перевели квартиру из жилого помещения в нежилое. Да, такая процедура есть. Но должны тогда выполняться все условия такого перехода. Для жилого помещения одни тарифы ЖКХ, а для нежилого – другие. В жилом помещении можно иметь прописку, а в нежилом – нельзя. Хотя сама квартира внешне, быть может, и не меняется при таком переоформлении. А Вы так легко не соблюдая никаких условий, бесцеремонно назвали уравнение функцией. С чего бы? Уже здесь ошибка. За неделю жду от Вас разбора этой ошибки и ее подтверждения. Что касается деления на 0. Вы как математический малыш под дурачка говорите: «Где в выражении 1/(2^2-4) я делю на 0? Я же не на 0 тут делю, а на (2^2-4). Где тут написано 0?» А у Вас вместо нуля стоят буквы, и чтобы «обмануть деление на 0» Вы одну букву заставляете стремиться к какому-то значению, чтобы благополучно воспользоваться правилом Лопиталя. Но у Вас ошибка даже раньше этого. Когда Вы уравнение назвали функцией без оговорок об условиях такого перехода. И Вы не написали даже подробного перехода от (6) к (7). А какой первый шаг будет. Это логарифмирование. И при такой операции при a=1 и целых x,y получится логарифм 0 в обеих частях уравнения. Даже еще до деления на 0 в уравнении (7), у Вас получается логарифм 0, т.е. минус бесконечность. Уже такую операцию Вы должны были делать, оговаривая, что значения при a=1 и целых x,y должны быть исключены, так как они уже не входят в область определения нового уравнения, полученного после логарифмирования обеих частей уравнения (6). Ваше доказательство неверно. Точка. Правильно. Не соглашайтесь с этим. Вы потеряете все. Все свои накопленные дивиденды за 30 лет. Вы станете математическим банкротом. Лучше уж дальше отрицать все и вся. Нет никакой ошибки и все. «У вас главное доказательство ошибочности нашего доказательства ВТФ – «Этого не может быть, потому что не может быть никогда»» - Это у Вас аргументация: «Я доказал теорему Ферма, потому что я не мог ее не доказать. Я ведь гений. Мы с сыном вместе гении.» А то что 300 лет ЛУЧШИЕ математики мира не могли доказать теорему Ферма это не аргумент. Это вообще ничего не значит. Видео посмотрите: https://yandex.ru/video/preview/1709784193270467366. Про Вас ведь видео. Даю опять неделю, чтобы разобраться. Не в вопросе как понимать «упрощенно деление на 0». А в вопросе перехода от уравнения (6) к неявной функции, которая затем стала явной (7). Здесь ошибка. И никакое правило Лопиталя, как волшебная таблетка от деления на 0, Вам не поможет. Разбирайтесь. Уже всем понятно, что Ваше доказательство ложно. Даже позвонившая Вам школьница, прочитав мои отзывы, поняла, что Ваше доказательство ложное. Это и следовало ожидать. Кстати из видео Вы поймете, почему никто не хочет из кандидатов и докторов наук связываться с Вашим доказательством и рецензировать его. У Вас нет доказательства. Посчитайте, сколько времени Вы потратили за 30 лет на него. А таких как Вы «доказавших» теорему Ферма тысячи, десятки тысяч. Только в эти новогодние праздники здесь опубликовали три «доказательства» теоремы Ферма. Вам не надоело изобретать вечный двигатель? Нельзя простыми методами доказать эту теорему. Слышите? Нельзя. Все. Разбирайтесь. Неделя.

22.01.2024, 21:49 Ремизов Вадим Григорьевич Отзыв:  Мистер Харт! Куда Вы пропали? Неделя уже прошла! Это не мне надо разбираться с переходом от (6) к (7). У меня то все ясно - Я неявную функцию (6) выражаю в явном виде (7). А вот, что Вы делаете никому не понятно. Так что не пропадайте, мы еще не начинали дискуссию. Свои посты давайте называть не утверждения №, а проблема №. Так что за Вами Проблема № 1 - деление на ноль. Свои проблемы формулируйте четко и по одной!

23.01.2024, 17:01 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Да, оказывается, Вы понятия не имеете о неявных уравнениях и неявных функциях, как говорят ни уха, ни рыла, а туда же. Небольшой ликбез. Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство. Когда равенство содержит две и более неизвестных, уравнение называется неявным, потому что решениями этого уравнения являются неявные функции. Неявное уравнение — это отношение вида R(x1, … , xn)=0, где R является функцией нескольких переменных. Неявная функция — это функция, заданная неявным уравнением как связь одной из переменных (значение) с другими переменными (аргументами). Явная функция у(х) задается формулой вида y=f (x), т. е. значение у вычисляется просто подстановкой х. Неявная функция у (х) задается уравнением вида f (x, y)=0, т. е. для вычисления ее значения надо решать уравнение. Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет вовсе (либо нет тех, что удовлетворяют заданным условиям). Ну, а далее, читайте букварь, учебники и ищите информацию в интернете, ликвидируйте пробелы в образовании. Это, во-первых. А, во-вторых, не знаю, по каким помойкам Вы рыскаете в поисках своих контрпримеров, которые не лезут ни в какие ворота. Вы приводите контрпример и сами не знаете, что вы хотите доказать своими контрпримерами. Например. Вы записали уравнение y^2=x, за тем получаете второе уравнение, исключив отрицательные значения корня y= - Sqrt(x). Вы фокусник! А, затем восклицаете – смотрите, первое уравнение имеет 5 решений, а второе – 3 решения, и делаете вывод, что наше доказательство ВТФ – ошибочно. А, рассуждения про ЖКХ – это вообще шедевр доказательства ошибочности нашего доказательства ВТФ. Мистер Харт, мы еще не решили проблему № 1 – «Есть ли в нашем доказательстве деление на ноль?» Почему Вы уходите от ответа на этот вопрос? Без ответа на этот вопрос, мы не можем идти дальше!

17.02.2024, 12:22 Ремизов Вадим Григорьевич Отзыв: Что же это такое? Никто не может написать рецензию на нашу статью и не оставить отзыв. На наше доказательство Великой теоремы Ферма нет замечаний и не обнаружено ошибок. Отсюда следует, что наше доказательство Великой теоремы Ферма – верное!

19.02.2024, 13:41 Харт Алекс Отзыв: "Куда Вы пропали?" - Я написал комментарий, а его не опубликовали. Пусть сами комментируют эту ошибочную статью.

19.02.2024, 16:49 Ремизов Вадим Григорьевич Отзыв: С мистером Хартом у меня старые счеты. Ранее он утверждал, что в нашем доказательстве ВТФ мы делим на ноль, поэтому наше доказательство ВТФ ошибочное. А когда мистера Харта уличили в невежестве (он не понимает разницы между делением на ноль и нахождением предела функции по правилу Лопиталя), то он отказывается признать, что ошибался! Мистер Харт Вы не умеете ясно и четко изъясняться, у Вас богатая фантазия, поэтому Ваши отзывы на несколько страниц и не устраивают модераторов. В них столько ошибочных утверждений и контрпримеров, что непонятно с чего начинать. Я Вам говорю, сначала признайте, что ошибались с делением на ноль, а потом формулируйте проблемы четко и ясно, по одной. Будем разбираться.

19.02.2024, 17:22 Харт Алекс Отзыв: "Ваши отзывы на несколько страниц и не устраивают модераторов" - Видимо мои отзывы, обличающие данную статью, не устраивают их тем, что они в итоге приведут к тому, что данная статья будет удалена. А она нужна здесь им. В плане того, что многие сюда заходят посмеяться. А каждый просмотр это деньги.

19.02.2024, 20:44 Ремизов Вадим Григорьевич Отзыв: Мистер Харт! Пока обличили только Вас, но Вы не желаете это признать. Не знаю, чего Вы добиваетесь. Вы не хотите понять, что обсуждать сразу несколько проблем одновременно нельзя. Поэтому еще раз заявляю Вам, что до тех пор, пока Вы не признаете, что ошибались, я с Вами не буду обсуждать Ваши ошибки! И еще хочу Вам сказать, никогда не употребляйте в доказательствах слово очевидно, поскольку все Ваши «очевидные опровержения» сразу становятся не очевидными, не верными и ошибочными опровержениями. И так, жду от Вас чистосердечного признания и формулировки проблемы № 2, то есть первого Вашего «очевидного опровержения». И еще, не надо обвинять в предвзятом отношении к Вам модераторов журнала, Вы не знаете к чему придраться.

20.02.2024, 22:52 Цорин Борис Иосифович Отзыв: О, г. Ремизов пошел на новую итерацию. Я-то думал, он тогда удалил статью, потому что осознал свою ошибку и раскаялся, но нет, вот она, статья с той же ошибкой. Напомню основную суть ошибки. {1} Нельзя сказать, что решением уравнения является функция. Решением (корнем) уравнения является кортеж (точка числового пространства, мерность которого совпадает с количеством неизвестных величин уравнения). Допустимо также называть решением множество корней уравнения, оговаривая это. {2} Пытаясь рассмотреть множество корней уравнения с несколькими неизвестными как функцию одной неизвестной от других, нельзя утверждать, что эта функция гарантированно существует и является непрерывной. Даже если эти уравнения получены дифференцированием непрерывной функции. Контрпримеры к утверждению г. Ремизова найти легко. Например, рассмотрев непрерывную и гладкую функцию f(x,y)=(x^2)*(y^2) и дифференцируя по х, мы получим необходимое условие экстремума 2x*(y^2)=0, множеством решений которого являются все точки вида (0;y0) и (x0;0) (они же являются и экстремумами функции), но это множество не образует ни функции y=f(x), ни функции x=f(y). Можно найти и примеры непрерывных и гладких функций, точки экстремума которых образуют функцию, но не непрерывную, например, f(x,y)=sin(2x-2arctg(y)-pi/2), у которой точки экстремума образуют функцию y=tg(x), имеющую бесконечное количество точек разрыва второго рода, а у функции f(x,y)=sin(x-arctg(y)-pi/2) решения необходимого условия экстремума df/dx=0 образует функцию y=tg(x). Таким образом, дальнейшие рассуждения г. Ремизова не имеют смысла, как исходящие из неверных посылок. {3} Но стоит учесть, что все словоблудие г. Ремизова про "функции необходимых условий" предназначено только для того, чтобы замаскировать основную его ошибку, которую (судя по его рассказам) он еще с девяностых лет двадцатого века пытается выдать за доказательство Великой Теоремы Ферма. Пытаясь преобразовать уравнение (6), г. Ремизов проводит преобразование, не являющееся тождественным, и получает равенство (7). Несомненно, если равенство (7) верно, то и равенство (6) обращается в 0, однако обратная зависимость отсутствует. Так как "А является необходимым условием В" означает, что из В следует А, то из наличия экстремума функции (2) в некой точке следует равенство (6). Таким образом, экстремум функции (2) в некой точке и выполнение равенства (7) в некой точке в равной мере являются посылками для равенства 6. Утверждение "Из B следует A, и из С следует A" не позволяет установить какую-либо связь между B и С, так что попытка вывести какую-то связь точек экстремума функции (2) и равенства (7) является логической ошибкой. {4} Отмечу также, что проводя преобразование (8), г. Ремизов одним махом исключил все случаи x=y, которые, конечно, не могут дать решение теоремы Ферма, но прекрасно дают решения уравнения (6). Если же г. Ремизов накладывает на функцию (2) условие "х!=y", то он тем самым исключает ее непрерывность. Впрочем, на фоне остальных ошибок эта показательна, но малозначительна. {5} Отмечу также, что если не заметить ошибок в рассуждениях г. Ремизова и принять все его рассуждения за верные, то получится, что он, во-первых, доказал, что при целых n>2 и a=1 функция (2) якобы не имеет точек экстремума вообще, а не только в целых числах, а во-вторых, что уравнение Ферма якобы не имеет целых решений при n=1 (смехотворно рассуждение про "функция (2) вырождается в линейное уравнение, в котором нет n", то, что она будет связана с этим уравнением, никак не мешает исследовать ее методами г. Ремизова, а "отсутствовать параметр n" начинает при подстановке на место этого параметра абсолютно любого значения). Впрочем, г. Ремизов, как я помню из его комментариев под прошлыми статьями, очень любит отрицать любые контрпримеры, сводя свое отрицание к "это другое", так что я уже не жду от него восприятия критики, а просто обращаю внимание читателей, рецензентов и модераторов на его ошибки. {6} P.S. Надеюсь, никто не предположил, что буквой "г." я сокращаю слово "господин".

21.02.2024, 10:24 Цорин Борис Иосифович Отзыв: Поправка к одному из примеров пункта {2} моего предыдущего комментария. У функции f(x,y)=sin(2x-2arctg(y)-pi/2) не точки экстремума, а точки минимума образуют функцию y=tg(x), это описка из-за многократного редактирования текста перед отправкой и невозможности в комментариях данного сайта создавать форматированный текст.

21.02.2024, 12:29 Ремизов Вадим Григорьевич Отзыв: Наконец-то дождались, в бой введена тяжелая артиллерия, в дискуссию вступил г.Цорин. Г. Цорин, Вы не лучше мистера Харта, Вы, как и он, написали отзыв на нескольких страницах, смешав все в одну кучу дерьма. Вы думаете, чем больше проблем Вы будите обсуждать сразу, тем более убедительны будут Ваши доводы. Лично я, сомневаюсь в этом. Чтобы дискутировать с Вами я задам Вам всего один вопрос – как Вы считаете, в нашем доказательстве ВТФ имеет место деление на ноль или не имеет? Это лакмусовая бумажка на Ваш статус – Вы фермафоб или объективный математик? Предупреждаю Вас, что я не буду даже рассматривать Ваши отзывы, если в них рассматривается больше одной проблемы (одного утверждения, одного контрпримера и т.д.). Отвечайте на проблему № 1 (о делении на ноль) и приводите Вашу проблему № 2.

21.02.2024, 19:02 Цорин Борис Иосифович Отзыв: Хотите по очереди? Не можете осилить чтение больше, чем нескольких предложений, за раз? Ок. {0} Про деление на 0. Вы накрутили в "доказательстве" кучу ерунды, чтобы в нем не звучало деление на 0, потому что изначально, еще в девяностых, пытаясь доказать теорему Ферма, разделили на 0, и с тех пор все усложняете и усложняете свои формулировки, допуская все новые и новые ошибки, потому что психологически не готовы признать, что ошиблись еще в самом первом своем доказательстве. В текущей версии того, что Вы называете доказательством, среди тех текстов, что имеет смысл анализировать, деление на 0 не озвучено. А теперь поехали повторять основные Ваши ошибки по очереди, более подробно.. {1} Вы пишете: "...являются неявными уравнениями, решениями которых являются явные и неявные функции...". Эта формулировка бессмысленна. Нельзя сказать, что решением уравнения является функция. Решением (корнем) уравнения является кортеж (упорядоченный набор чисел, т.е. точка числового пространства, мерность которого совпадает с количеством неизвестных величин уравнения). Допустимо также называть решением множество корней уравнения, оговаривая это. В школьном курсе "решением уравнения" называют процесс поиска корней и доказательство, что найдены все корни (или что их нет). Ни одно из значений словосочетания "решение уравнения" не означает какую-либо функцию. Возможно (гипотезы на основе Ваших комментариев к прошлой версии Вашей "статьи"), Вы имели в виду, что множество корней уравнения является функциональным отношением, и рассматриваете заданную им функцию, или что множество корней уравнения включает в себя функциональное отношение как подмножество? Если это так, то уточните, какая из двух моих гипотез о Ваших формулировках верна, то есть рассматриваете ли Вы функцию, заданную функциональным отношением, равным множеству корней уравнения, либо же являющимся его подмножеством, и мы перейдем к следующей ошибке, формулировка которой будет зависеть от Вашего выбора (а суть останется одной и той же). Если же Вы имели в виду что-то иное, сформулируйте свое "уравнения, решениями которых являются функции" с использованием общепринятого языка математики.

21.02.2024, 23:42 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, я не позволю Вам закусывать яблоки! Так дело не пойдет. Была сформулирована проблема № 1 – “”имеет место в доказательстве деление на ноль или не имеет?”” Так вот, пока Вы не ответите на этот вопрос, я не буду разъяснять Вам Ваши опусы! И пожалуйста, обозначайте проблемы с № с формулировкой заключенной в двойные кавычки – “”…””, чтобы было ясно, где начинается формулировка проблемы и где кончается! Не обозначайте номер проблемы в фигурных скобках – {…}. Озвучена проблема № 1, ответа на нее мистер Харт не дал, но это не означает, что проблема останется без ответа. Мистер Харт не дает ответа, то ответ должны дать Вы! У мистера Харта не хватает мужества признать свою ошибку, тогда изобличать Харьта будете Вы, либо сами будите подписываться под ошибкой.

22.02.2024, 6:07 Цорин Борис Иосифович Отзыв: Я ответил. Вы не смогли это прочитать? Вам действительно нельзя давать тексты длиннее пары строк, Вы их не можете осилить? Ок, коротко. Сейчас в тексте деления на 0 нет, раньше (в прошлой статье) было.

22.02.2024, 11:16 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, во всех моих статьях формулы одни и те же, только я по-разному пытался объяснить Вам переход от формулы (6) к формуле (7). Поэтому непонятен Ваш вывод – «Сейчас в тексте деления на 0 нет, раньше (в прошлой статье) было». Да, во всех моих статьях в тексте не было деления на ноль. Я нигде не говорил и не писал, что делю на ноль, я говорил, что нахожу предел функции по правилу Лопиталя. Это мистер Харт говорил, что я делю на ноль, чтобы доказать ошибочность нашего доказательства ВТФ. Не надо отмазывать невежество мистера Харта, то он говорил, что я делю на ноль, то он не говорил, что я делю на ноль. Так было деление на ноль, или не было деления на ноль? У Вас не поймешь. Если Вы согласны с тем, что мистер Харт ошибочно указывал на деление на ноль в нашем доказательстве ВТФ, то мы можем переходить к проблеме № 2, а если Вы не согласны, то мне придется еще раз объяснять Вам, что в нашем доказательстве никогда не было деления на ноль! Ни в этой статье и ни во всех других статьях не было деления на ноль!

22.02.2024, 17:31 Цорин Борис Иосифович Отзыв: Мне неинтересно Ваше объяснение про деление на 0. В текущей версии статьи она превратилась в ненаучную фантазию куда раньше, чем дошла до того момента, которое Харт предпочитает называть делением на 0, поэтому спор о том, можно ли это называть делением на 0, бессмысленен. Про "уравнения, решениями которых являются функции" рассказывать будете или восемь строк Вы не осилили и надо покороче проблему описать? Если надо покороче, то сколько строк Вы способны прочитать, не сбиваясь на обсуждение деления на 0?

25.02.2024, 13:13 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, мне показалось, что Вы эрудированный и знающий математик, но это не так! Поскольку Вы изъясняетесь на изоповом языке. Вы так же, как и мистер Харт, не понимаете отличие деления на ноль от нахождения предела функции при раскрытии неопределенности типа 0/0. Вы утверждаете, что в тексте деления на 0 нет, раньше (в прошлой статье) было. Может быть, поясните, что же это такое – в тексте деление на 0. Поэтому Вам и неинтересно наше объяснение про деление на 0. И так, с Вами все ясно, когда Вам выгодно, деление на 0 есть, а когда невыгодно – деления на 0 нет. Вы оба, вместе с мистеров Хартом считаете, что в нашем доказательстве мы делим на ноль, и что в этом и заключается ошибка в доказательстве ВТФ. Однако признаться в этом не желаете и поэтому Вы считаете, что спор о, так называемом, делением на 0, бессмысленен. Будем считать, что с проблемой № 1 разобрались. Теперь переходим к проблеме № 2. Господин Цорин, Вы считаете, что уравнения, содержащие больше одной неизвестной, не являются неявными уравнениями, решениями которых являются явные и неявные функции... и что эта формулировка бессмысленна, и что нельзя сказать, что решением уравнения является функция. ". Ну а дальше у Вас начинаются инсинуации и понос про кортежи, про точки числового пространства, мерность которого совпадает с количеством неизвестных величин, про множество корней уравнения, про функциональное отношение. Господин Цорин, Вы иезуит, Вы требуете изъясняться на общепризнанном языке математики. А сами, на каком языке Вы изъясняетесь? Пытаетесь пустить пыль в глаза, показать свою ерундиции, сбить с толку оппонентов. Не буду с Вами спорить, это бесполезно, приведу лишь определения из Википедии. Неявная функция — это функция, заданная неявным уравнением как связь одной из переменных с другими переменными (аргументами). Неявные функции – Определение: Функция y = y(x), где x = (x1, ..., xn), называется неявной функцией, заданной уравнением F (x, y) = 0, если выполняется равенство F (x, y(x)) = 0. Если Вы ничего не хотите понимать, то привожу для непонимающих: необходимое условие существования экстремума функции (2) уравнение (6), является неявным уравнением, решением которого является неявная функция (7), выраженная в явном виде, и которую при а=1 надо доопределить значением n из диофантова уравнения Ферма (1) и функции (2).

25.02.2024, 17:51 Цорин Борис Иосифович Отзыв: Вы приводите из википедии определение "неявной функции, заданной уравнением" в ответ на вопрос, что Вы понимаете под "функцией, являющейся решением уравнения". Если это ответ на заданный вопрос, то под "функцией, являющейся решением уравнения" Вы в тексте статьи и дальнейших комментариях понимаете "функцию, заданную уравнением", то есть функцию, при подстановке в уравнение превращающую его в тождество. Это так? Ответьте "Да" или "Нет" (или начните ответ с одного из этих слов, если не сможете ответить коротко).

26.02.2024, 14:44 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, я вообще не понимаю, о каких функциях Вы говорите, если это не неявные функции, которые определены в Википедии. Вы мне задаете вопрос – что я понимаю под "функцией, являющейся решением уравнения”? Это я должен спросить Вас - что Вы понимаю под "функцией, являющейся решением уравнения”? Я Вам объяснил, что я понимаю под неявными функциями, определяемыми неявными уравнениями. Оказывается, что Вы понятия не имеете о неявных уравнениях. Поэтому Вы и утверждаете, что нельзя сказать, что решением уравнения является функция, что эта формулировка бессмысленна. Неявная функция (7) n=n(a), выраженная в явном виде, является решением неявного уравнения (6). Неявная функция (7) в а=1 неопределена, поэтому функция (7) в этой точке должна быть доопределена значением n, равным значению n в диофантовом уравнении Ферма (1). Неявная функция (7) везде в области определения функции (2) больше нуля, поэтому Ваш контрпример у2=х с отрицательными значениями корня неуместен. Вы вводите какие-то неопределенные функции, являющимися решениями неизвестно каких уравнений, и требуете, чтобы я сказал, что я под ними понимаю и подразумеваю. Это Вы должны нам это объяснить. Поэтому не скажу Вам, ни да, ни нет. А вообще, то, что Вы написали в последнем отзыве, это типичная тавтология. Господин Цорин, я не понимаю, какое отношение имеют Ваши функции, определяемые неизвестно какими уравнениями, к верности нашего доказательства ВТФ. Поэтому пора завязывать с Вашей проблемой № 2. Теперь моя очередь сформулировать свою проблему. Вот формулировка Проблемы № 3 – “”Как Вы считаете, что при вычислении предела функции (8), надо или не надо учитывать зависимость переменных хо и уо от параметра а“”.

28.02.2024, 10:03 Цорин Борис Иосифович Отзыв: "Решение уравнения" и "функция, заданная уравнением" - это разные термины. Я осознаю, что Вы не владеете математической терминологией и не понимаете, зачем она нужна, поэтому терпеливо отношусь к Вашей агрессии. Перечитайте мой предыдущий отзыв. Он короткий, всего три строчки, у Вас есть шанс справиться с этим заданием. Ответьте на заданный в нем вопрос.

28.02.2024, 13:00 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, Вы чего пристали как банный лист к заднице. Еще раз заявляю Вам, что функция (7) является неявной функцией, определяемой неявным уравнением (6)! Не пытайтесь запутать меня, это Вам не удастся. Все вопросы адресуйте к авторам учебников по математике. Если Вы не понимаете, что такое неявная функция и неявное уравнения, даю Вам пояснения из учебников по математике. Функция y = y(x), где x = (x1, ..., xn), называется неявной функцией, заданной уравнением F (x, y) = 0, если выполняется равенство F (x, y(x)) = 0. Рассмотрим уравнение F(x1, . . . , xn, y) = 0. Решение этого уравнения относительно y является функцией n переменных. y = f(x1, . . . , xn) и называется неявной функцией, определяемой уравнением F(x1, . . . , xn, y) = 0. Если выполняется равенство F (x, f(x)) = 0, то функция f называется неявной функцией, определенной уравнением F(x,y) = 0. Говорят также, что функция f задана неявно уравнением F(x,y) = 0. О функции f(x) говорят как о неявной функции, или неявно заданной функции. Неявно заданные функции - это такие функции, которые определены уравнением вида F(x,y)=0. В отличие от обычных функций y=f(x), здесь переменная y задается не явно через x, а косвенно через решение уравнения. Явная функция у (х) задается формулой вида y=f(x), т. е. значение у вычисляется просто подстановкой х. Неявная функция у (х) задается уравнением вида f(x,y)=0, т. е. для вычисления ее значения надо решать уравнение. Все, больше я с Вами не буду дискутировать на эту тему! Пожалуйста, ответьте - да или нет на вопрос в проблеме № 3. А после формулируйте свою проблему № 4.

28.02.2024, 14:21 Цорин Борис Иосифович Отзыв: Меня мало интересует функция (7) и уравнение (6), потому что у Вас ошибки не в самой функции (7), а в том, что Вы считаете теорией, на которую опираетесь. Вы так и не ответили четко на заданный вопрос, но, допустим, повтор определения в расширенном виде я зачту за положительный ответ. То, что Вы называете "проблемой 3", я не считаю проблемой: Вы верно вычислили предел в (8) при условии х0!=y0. Этого ответа Вам достаточно? А теперь вернемся к теории. Вы согласны, что если некая функция y=f(x1,...,xn) неявно задана уравнением F(x1,..,xn,y)=0, то это уравнение может иметь и другие корни, то есть корни, не удовлетворяющие равенству y=f(x1,...,xn)?

28.02.2024, 17:53 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, почему Вы все время пытаетесь увести решение проблемы о верности нашего доказательства ВТФ в сторону, к обсуждению какой-то теории. Вы, вместо того, чтобы указать, где в нашем доказательстве ВТФ ошибки и привести доказательства ошибочности доказательства нашего ВТФ, начинаете бессмысленную дискуссию ни о чем. Вы пишете, что зачтете мое утверждение о неявной функции (7) за положительный ответ. Ну, и что из этого, какое это имеет отношение к ошибочности нашего доказательства ВТФ? Поясните как понимать х0!=y0, эту абракадабру? Теперь относительно проблемы № 3. Я правильно понял, что Вы считаете, что переменные х0 и у0 не зависят от параметра “а”? такой ответ меня удовлетворяет. Давайте не будем погружаться в дерби теории. У нас конкретная неявная функция (7) и конкретное неявное уравнение (6), вот и приведите лишние корни, не удовлетворяющие неявной функции (7). Кончайте тянуть кота за хвост, прямо укажите, где ошибка и в чем ошибка! Сформулируйте проблему № 4.

28.02.2024, 21:21 Цорин Борис Иосифович Отзыв: {Ответы на Ваши вопросы} "Почему Вы все время пытаетесь увести решение проблемы о верности нашего доказательства ВТФ в сторону, к обсуждению какой-то теории" - потому что любое математическое доказательство - это цепочка умозаключений, исходящих из определений, аксиом и теорем. У Вас нет ошибок непосредственно в преобразованиях, у Вас есть ошибки в использованных посылках умозаключений. "Вы, вместо того, чтобы указать, где в нашем доказательстве ВТФ ошибки..." - чтобы указать, где точно в Вашем доказательстве ошибка, нужно понять, что Вы имели в виду. Если бы Вы владели математической терминологией и использовали ее корректно, а при доказательстве ссылались на теоремы, было бы легче просто ткнуть пальцем в ошибку. "Поясните как понимать х0!=y0" - комбинация "!=" означает "не равно". Если хотите, могу как знак "не равно" использовать "<>" вместо "!=", это тоже распространенное обозначение. {Продолжение обсуждения проблемы, которой Вы дали номер 4} Предположим, что у нас есть произвольная непрерывная гладкая функция f(x1,...,xn,y), а у этой функции есть необходимое условие экстремума - уравнение F1(x1,...,xn,y)=0, которое задает непрерывную неявную функцию y=f2(x1,...,xn). Верно ли я понял, что Вы согласны, что могут быть другие корни уравнения F1(x1,...,xn,y)=0, не удовлетворяющие равенству y=f2(x1,...,xn), но утверждаете, что эти другие корни не могут являться точками экстремума функции f?

29.02.2024, 11:29 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, я ничего не утверждаю! Это Вы утверждаете и приписываете мне свои утверждения. У нас имеются конкретные функции: функция (2); необходимые условия существования экстремумов (4), (5) и (6); неявная функция (7). Там есть переменные - х,у параметры - n,а, и нет переменных х1 и т.д. Или возьмите функции из контрпримеров мистера Харта. И на их примере сформулируйте проблему № 4. Укажите конкретно, какие имеются лишние корни. Я нигде не утверждал, что новая теория решения диофантовых уравнений (теория доказательства отсутствия целочисленных решений у диофантовых уравнений) применима для всех диофантовых уравнений. Мы с Вами уже 10 дней толчем воду в ступе, а воз и ныне там! Сформулируйте ясно и четко на проблему № 4, чтобы было понятно, где ошибка и в чем состоит ошибка.

29.02.2024, 18:22 Цорин Борис Иосифович Отзыв: {1, ПОВТОРЯЮ ВОПРОС, ответьте "a)Нет", "a)Да, b)Да" либо "a)Да, b)Нет"} Предположим, что у нас есть произвольная непрерывная гладкая функция f(x1,...,xn,y), а у этой функции есть необходимое условие экстремума - уравнение F1(x1,...,xn,y)=0, которое задает непрерывную неявную функцию y=f2(x1,...,xn). a) Как вы считаете, могут ли быть другие корни уравнения F1(x1,...,xn,y)=0, не удовлетворяющие равенству y=f2(x1,...,xn)? b) Если они могут быть, то могут ли они являться точками экстремума функции f? {2} "Мы толчем воду в ступе", потому что Вы изо всех сил отказываетесь отвечать на вопросы. Чтобы сформулировать проблему "№4", мне нужно точно понимать Ваши очень коряво сформулированные утверждения. Пока Вы не ответите на мои вопросы, мы не сможем двигаться дальше. Как только Вы четко ответите на мои вопросы, я смогу сформулировать проблему. Если хотя бы один из ответов окажется "Нет", я смогу сразу сформулировать проблему "№4", если же Вашим ответом будет "Да, Да", мне придется продолжить уточнять теоретические основы Вашего доказательства. Если Вам что-то непонятно в вопросе, или Вы считаете, что в нем не хватает данных, задайте уточняющий вопрос. Если же Вы продолжите просто отказываться от ответов на мои вопросы, требуя обсуждать что-то, кроме основной Вашей ошибки, мне придется предположить, что Вы сами прекрасно осознаете свою ошибку, но изо всех сил увиливаете от ее признания. {3} Оставляю временно без ответа часть Ваших слов, чтобы Вы не решили, что можно не отвечать на основной вопрос, а ответить только на все остальное. Ответьте на вопрос {1}, по возможности без лишних высказываний.

29.02.2024, 19:49 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, я Вам уже говорил, что новый метод решения диофантовых уравнений пригоден для решения не всех диофантовых уравнений. Поэтому при использовании произвольной функции нельзя ни доказать, ни опровергнуть доказательство ВТФ. Неужели вы этого не понимаете, и поэтому пытаетесь, используя неопределенную функцию общего вида, доказать, что наше доказательство ВТФ ошибочно. Поэтому и не собираюсь отвечать на Ваши вопросы, поскольку этот путь бесперспективный, это Сизифов труд, и потому, что я не на допросе. Все говорит о том, что Вы не знаете, где ошибка в нашем доказательстве, поскольку не можете кратко изложить, указать и сформулировать, где в нашем доказательстве ВТФ ошибка. Так что, если Вы считаете, что наше доказательство ошибочно, то изложите кратко ошибку в проблему № 4.

29.02.2024, 20:55 Цорин Борис Иосифович Отзыв: {1} Вы пишете: "...новый метод решения диофантовых уравнений пригоден для решения не всех диофантовых уравнений". А от того, применяем ли мы функции для решения диофантовых уравнений или исследуем их просто так, их свойства не зависят. Вы в первом же предложении пишете: "основано на свойствах экстремумов непрерывных и гладких функций [1, 93 – 161 c, 197 – 222 c], у которых в точках экстремумов функции экстремумов являются непрерывными функциями". Вот в трактовке свойств у Вас и ошибка. {2} Кратко: Проблема №4 состоит в том, что Вы при доказательстве используете "свойства функций", которых у функций на самом деле нет. Утверждение "У непрерывной и гладкой функции в точках экстремумов функции экстремумов не имеют разрывов и являются непрерывными функциями" ложно. Вам контрпримеры нужны или снова будете, как в прошлой статье, не читая их, вопить, что это не Ваша функция (2), поэтому это не контрпример, а для Вашей функции (2) верны все свойства, которые Вам хочется? ))) {3} Если нужны, то даю пример, максимально близкий к Вашему, его Вам давали и к прошлой статье. Рассмотрим f(x,y)=sin^2(Pi*a*(x^n+y^n)) +sin^2(pi*a*x)+sin^2(pi*a*y), где x,y>0 - положительные вещественные переменные, n>1 - положительный вещественный параметр, а - вещественный параметр с областью определения в точке а=1 и ее ближайшей окрестности. Дифференцируем эту функцию, получим необходимые условия экстремумов Pi*a*n*x^(n-1)*sin(2*Pi*a*(x^n+y^n)) + pi*a*sin(2*pi*a*x)=0 и Pi*a*n*y^(n-1)*sin(2*Pi*a*(x^n+y^n)) + pi*a*sin(2*pi*a*y)=0. Преобразованиями получаем еще одно необходимое условие экстремума y^(n-1)*sin(2*pi*a*x) - sin(2*pi*a*y)*x^(n-1)=0. Ой, а такое условие экстремума Вы исследовали и получили, что Ваши "функции экстремумов не имеют разрывов" только если при a=1 выполняется n=2. Если бы Ваше утверждение "У непрерывной и гладкой функции в точках экстремумов функции экстремумов не имеют разрывов и являются непрерывными функциями" было истинно, то все функции, для которых y^(n-1)*sin(2*pi*a*x) - sin(2*pi*a*y)*x^(n-1)=0 является необходимым условием экстремума, не имели бы экстремумов при n>2 и a=1. Но вот проблема: при любом целом n и a=1 рассматриваемая мной функция имеет глобальный минимум в любых целых x и y, так как обращается в них в ноль. Следовательно, предположение неверно, Ваше утверждение ложно, Ваша статья базируется на ложном утверждении и не доказывает ничего хорошего.

1.03.2024, 12:30 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, ответ на Ваш контрпример дам несколько позже. А теперь про n=1. Ну, что же Вы поскромничали и написали n>1, сразу могли и написать n>=1. Одним ударом прикончили бы и облили грязью и исключение случая n=1 из общего случая. Интересно, а как Вы относитесь к исключению случая n=1 из общего случая, надо было ли рассматривать эти случаи отдельно?

1.03.2024, 16:06 Цорин Борис Иосифович Отзыв: {1} Ваше исключение n=1 по причине "нелинейная функция (2) вырождается в линейное диофантово уравнение z=x+y, в котором отсутствует параметр n" с точки зрения математики является бессмыслицей. При любом конкретном значении n функция (2) превратится в функцию, в которой отсутствует параметр n, не только при значении n=1. {2} Кроме того, отмечу, что Вы забыли придумать какую-нибудь бредовую "причину" исключить нецелые значения n, а ведь функция (2) при многих (счётное количество) нецелых значениях параметра n вполне будет иметь глобальные минимумы в целочисленных точках (x0, y0), хотя и не нулевые. Ну так производные, а Вы анализируете только их, в принципе не могут помочь отличить нулевые минимумы от ненулевых. {3} Но и случай n=1, и случаи нецелых n всего лишь подтверждают, что Ваше "доказательство" имеет ошибки, а суть этой ошибки я назвал в прошлом сообщении. Ну а если Вы хотите узнать, почему эту ошибку Вы допустили, то отвечайте все-таки на заданные вопросы. {4} "Одним ударом прикончили бы и облили грязью" - во-первых, грязью постоянно поливали в сообщениях Вы, а я от грязи стараюсь держаться на расстоянии. Во-вторых, Вы же сами просили подавать по одной проблеме за раз, а теперь недовольны, что я назвал одну?

1.03.2024, 18:18 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, я уже имел опыт общения с Вами, когда Вы рассматривали несколько проблем одновременно. Когда Вас прижимали, Вы начинали рассматривать другую проблему, не давая ответа на первую. Поэтому я и выставил требование – рассматривать только одну проблему, чтобы можно было ее рассмотреть полностью и до конца. Как я понял, Вы утверждаете, что функция (2) при нецелых значениях параметра “n” имеет экстремумы в целочисленных точках (x0, y0). Я правильно понял Вас?

1.03.2024, 19:26 Цорин Борис Иосифович Отзыв: {1. Ответ на инсвинуации.} "Поэтому я и выставил требование – рассматривать только одну проблему, чтобы можно было ее рассмотреть полностью и до конца. Как я понял, Вы утверждаете, что функция (2)..." - что-то Вы сами одни проблемы отказываетесь рассматривать (на вопросы по теории так и не ответили), вторые бросаете, обещая ответить позже (эту я на "проблему 4" намекаю, да и "n=1" Вас что-то перестало интересовать), и переходите к новым... А врете, что это я так делаю. {2. Ответ на вопрос.} "Как я понял, Вы утверждаете, что функция (2) при нецелых значениях параметра “n” имеет экстремумы в целочисленных точках (x0, y0). Я правильно понял Вас?" - не знаю, как Вы меня поняли, поэтому даю точную математическую формулировку. При любых целых x0 и y0, больших единицы, можно найти такое вещественное n0, большее единицы, что при n=n0 и a=1 функция (2) будет иметь в (x0,y0) глобальный минимум, не равный 0. {3. Доказательство к п.2} Для нахождения такового n0 достаточно выбрать любое целое z0 такое, что x0<z0, y0<z0, z0<x0+y0 и решить уравнение x0^n+y0^n=z0^n, где x0, y0 и z0 - выбранные числа, а n - неизвестная. Это уравнение гарантированно имеет корень n0, больший 1, так как слева и справа в уравнении находятся выражения, являющиеся непрерывными функциями от n, при n=1 левая часть больше правой, а при n, стремящемся к плюс бесконечности, правая часть больше левой. Если мы у функции (2) устанавливаем параметру n значение n0, то при x=x0 и y=y0 z будет равно z0, то есть целому числу. Так как a=1 и n=n0, то первые три слагаемых функции (2) при x=x0 и y=y0 обращаются в 0, а четвертое является константой. Так как первые три слагаемых не могут быть меньше 0, а четвертое является константой, функция достигает при x=x0 и y=y0 наименьшего возможного значения при данных значениях параметров, то есть в этой точке у нее глобальный минимум. На всякий случай (вдруг Вы сейчас возьмете и принципиально забудете) напоминаю: определение минимума не требует, чтобы при изменении ПАРАМЕТРА значение функции не могло уменьшиться, параметр отличается от переменной именно тем, что при исследовании функции считается величиной фиксированной (из любимой Вами Википедии: параметр - "величина, неизменная в данной задаче либо для данной кривой, но не являющаяся универсальной константой"). {4. Предложение, связанное с данной темой.} Если Вы согласитесь считать и называть a и n не параметрами, а переменными, и внесете все необходимые изменения в Вашу "статью", то случаи минимумов при нецелых n исчезнут или как минимум станут труднонаходимыми и труднодоказуемыми. Это никак не исправит и не скроет Вашу основную ошибку, зато лишит меня одного (и только одного) из примеров очевидных нелепостей в Вашей "статье", а Вас лишит возможности отвергать контрпримеры на основании "тут нет параметров, одни переменные".

4.03.2024, 16:22 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, когда Вам задаешь прямой вопрос, когда не надо нести пургу, Вы сразу встаете в ступор. Неужели трудно ответить, да, Вы правильно меня поняли, или нет, Вы, неправильно меня поняли, не срываясь в демагогию. Дело вот в чем, я не понимаю, какое отношение имеют экстремумы функции (2) при нецелых n к нашему доказательству ВТФ. Ведь в доказательстве используются только целые значения n. Пожалуйста, поясните этот момент.

5.03.2024, 6:24 Цорин Борис Иосифович Отзыв: {1} "Неужели трудно ответить, да, Вы правильно меня поняли, или нет, Вы, неправильно меня поняли, не срываясь в демагогию" - так откуда же мне знать, правильно ли Вы меня поняли. Кстати, а Вы хоть раз ответили просто "да" или "нет"? А ведь я, в отличие от Вас, формулирую вопросы математически корректно. {2} "Ведь в доказательстве используются только целые значения n" - даю цитату из Вашей статьи: "В функции (2) x, y > 0 – положительные вещественные переменные, n > 1 – положительный вещественный параметр". Кстати, если Вы сейчас измените в статье n на целое, то "функция экстремумов (7) n=n(a)" вообще перестанет существовать - она же принимает нецелые значения. Ну а то, что в ВТФ n целое, к Вашим ошибкам отношения не имеет: ошибки я демонстрирую в Вашем "доказательстве" того, что функция (2) якобы может иметь экстремумы только при n=2, они там есть вне зависимости от того, используете ли Вы анализ функций для попытки доказательства ВТФ или просто так.

5.03.2024, 13:07 Ремизов Вадим Григорьевич Отзыв: Господин Цорин! В функции (2) параметры “a” и “n” могут изменяться в области их определения (как и переменные “х” и “у”). Но нас интересуют только минимумы функции (2) при изменении координат “х” и “у”, поэтому переменные “a” и “n” и рассматриваются как изменяемые параметры. Уравнение x0^n+y0^n=z0^n, где x0, y0 и z0 - выбранные числа, а n – неизвестная, имеет решение n0. Вы справедливо утверждаете, что «это уравнение гарантированно имеет корень n0, больший 1, так как слева и справа в уравнении находятся выражения, являющиеся непрерывными функциями от n». Но кто Вам сказал, что корень этого уравнения - n0, доставляет и минимум функции (2) при нецелых значениях n0, более того, функция (2) не может иметь минимумы при нецелых значениях n0 в точках с целыми x0, y0 при а=1 и любых значениях “z”. Докажем это! Когда “z” не целое, необходимые условия существования экстремумов (4) и (5) не удовлетворяются, поэтому функция (2) в этих точках не может иметь экстремумы. Осталось это доказать, когда “z” – целое. В этом случае, в функции (2) второе и третье слагаемые, независимо от значения n, равны нулю, поэтому в этих точках функция (2) принимает вид f(x,y)=(sin(pi*a*z)^2 + (sin(pi*n))^2. Поскольку первое слагаемое при a=1 и целом “z” равно нулю, то есть это слагаемое имеет минимум, поэтому производная этого слагаемого по “n” равна нулю. А производная второго слагаемого по “n” в точках минимума функции (2) равна pi*cos(2*pi*n) <>0 при нецелом “n”. Поскольку производная двух слагаемых равна сумме производных слагаемых, поэтому df/dn<>0, и поэтому f(x,y) в этой точке не может иметь минимума. Таким образом доказали, что функция (2) при нецелых n не может иметь минимумов, и что функция (2) может иметь минимумы только при целых n. А Вы утверждаете обратное! Так, кто же из нас прав7

5.03.2024, 14:41 Ремизов Вадим Григорьевич Отзыв: Извиняюсь, описался. "А производная второго слагаемого по “n” в точках минимума функции (2) равна pi*sin(2*pi*n) <>0 при нецелом “n”". и "А Вы утверждаете обратное! Так, кто же из нас прав?"

5.03.2024, 16:01 Цорин Борис Иосифович Отзыв: Естественно, прав я. Ваша главная ошибка в последнем наборе утверждений начинается со слов "производная этого слагаемого по “n”". Равенство "производной по параметру" нулю не является необходимым условием существования экстремума. Необходимым условием существования в точке экстремума функции нескольких переменных является равенство в этой точке нулю частных производных по всем переменным. НЕ по параметрам. Упрощая ситуацию до функции одной переменной: Вы же, надеюсь, не будете утверждать, что у функции f(x)=x^2+c, где c - вещественный параметр, необходимым условием существования экстремума будет равенство нулю производной по c, и что эта функция в результате не будет иметь экстремумов? )

5.03.2024, 19:30 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, а я считаю, что я прав, а не Вы! Так как мы задаем, что при а=1 переменные x0, y0 и z0 целыми и не изменяемыми, поэтому первые три слагаемых в функции (2) равны нулю и не изменяются. Тогда функция (2) будет равна f(x,y)=(sin(pi*n))^2 и будет зависеть только от параметра n. Или Вы считаете, что функция (2) и экстремумы функции (2) не зависит от параметра n. В точке нецелого n=n0 f(x, y, n)<>0 при этом df/dn<>0, поэтому f(x, y, n) в этой точке не может иметь минимума. Функция (2) может иметь нулевые минимумы только при целых n. Еще раз, кто Вам сказал, что корень n0 уравнения x0^n+y0^n=z0^n, доставляет и минимум функции (2) при нецелых значениях n0. Вы этого не доказали. Непонятно о каких минимумах Вы говорите? Теперь о функции f(x)=x^2+c. Если Вы зафиксируете координату точки экстремума х=х0=0, то функция экстремумов f(x)=x0^2+c не будет иметь экстремумов!

6.03.2024, 8:55 Цорин Борис Иосифович Отзыв: Еще раз. Вашими же словами: "Нас интересуют только минимумы функции (2) при изменении координат “х” и “у”". Чуете? Только при изменении х и y, а не при изменении n. При подстановке значений x0 и y0 функция получает конкретное значение. Это значение зависит от значений параметров, но это уже значение функции (2) в точке, а не функция (2). "f(x, y, n) в этой точке не может иметь минимума" - это верное утверждение, но n - это параметр, а не переменная, и никакой "f(x, y, n)" у Вас в статье нет, у Вас есть f(x, y), которая минимум имеет. Аналогично f(x0)=x0^2+c=0^2+c=0+c=c - это не функция, это значение функции f(x) в точке минимума. Если после этого Вы начнете рассматривать f(c)=c, это будет уже совсем другая функция, не имеющая отношения к поиску точки экстремума функции f(x)=x^2+c, а имеющая отношение только к определению значения функции в уже найденной точке экстремума. А если Вы, как написали, рассматриваете f(x)=c, то это еще одна функция, которая, кстати, является константой, и имеет экстремум (нестрогий) вообще в каждой точке, но эта функция к исходной f(x)=x^2+c отношения не имеет, не считая того, что является уравнением касательной к графику функции в точке экстремума, что Вы вряд ли подразумевали. У Вас явные проблемы с пониманием того, чем параметр отличается от переменной. В математическом анализе параметр - это некая величина, которая считается фиксированной, но не определенной однозначно. Если у нас есть функция или уравнение с параметрами, то это равносильно тому, что у нас было бы множество однотипных функций/уравнений, отличающихся значениями параметров. При исследовании функции или решении уравнения мы представляем себе, что параметр - это некое неизвестное нам число. Но число, а не переменная. Получив ответ, мы выражаем этот ответ через параметр, но не начинаем дальше считать этот параметр переменной. Решая уравнение ax^2+bx+c=0, где a,b,c - параметры, и a не равно 0, мы получаем x1=(-b-sqrt(b^2-4ac))/(2a) и x2=(-b+sqrt(b^2-4ac))/(2a), и делаем вывод, что корни есть только при b^2-4ac>=0, но мы не бросаемся утверждать, что корнем уравнения является какая-то функция, мы либо каким-то способом узнаем конкретные значения a,b,c и подставляем их, либо оставляем так, в виде формулы корня. Формулы, а не функции, потому что здесь нет переменных, только параметры. Когда мы ищем экстремум функции f(x)=x^2+С, где С - параметр, мы находим, что функция имеет минимум в точке 0, и что значение функции в точке минимума равно С, но мы не бросаемся менять С и искать, когда же само С оказывается минимальным, если перед нами стояла только задача найти саму точку минимума. У Вас получилось что-нибудь понять с подробного объяснения, или "аксиома Ремизова" помешала?

6.03.2024, 9:18 Цорин Борис Иосифович Отзыв: На всякий случай добавлю про производные. Откуда вообще берется необходимое условие экстремума? Если не стараться строго математически формулировать, а объяснять на пальцах, то производная - это выражение скорости изменения функции. Частная производная функции нескольких переменных - выражение скорости изменения функции при изменении одной конкретной переменной. Если частная производная в точке положительна, то при увеличении этой конкретной переменной функция возрастает и у нее не может быть экстремума в этой точке. Если частная производная в точке отрицательна, то при увеличении этой конкретной переменной функция убывает и у нее не может быть экстремума в этой точке. О том, что происходит, когда увеличиваются сразу две переменных, частная производная ничего не говорит, поэтому (и не только поэтому) равенство нулю частных производных по всем переменным - необходимое условие экстремума, но не достаточное. Но вот если мы берем производную по параметру, то мы начинаем изучать, что же происходит со значением функции, когда меняется параметр. А это к понятию экстремума отношения не имеет, даже Вы сами подтверждали, что "нас интересуют только минимумы функции (2) при изменении координат “х” и “у”".

6.03.2024, 11:00 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, Вам не нравится, что я назвал “n” и “a” изменяемыми параметрами, то называйте их переменными, то есть функция (2) будет у нас функцией 4 переменных. Возможно, это будет точнее. Это ничего не меняет! Повторяя в третий раз! Кто Вам сказал, что корень n0 уравнения x0^n+y0^n=z0^n, доставляет и минимум функции (2) при нецелых значениях n0. О каких экстремумах идет речь, когда Вы говорите, что функция (2) при нецелых значениях параметра “n” имеет экстремумы в целочисленных точках (x0, y0). И не надо вот таких контрпримеров, как f(x)=x^2+c, (лучше было бы f(x, у)=x^2+у, но их тоже не надо). И не надо путать координату экстремума со значением функции в точке экстремума. Господин Цорин, стоило задать Вам уточняющий вопрос, как Вы поплыли, вся Ваша стройная теория доказательства ошибочности нашего доказательства ВТФ посыпалась! Теперь осталось проверить, способны ли Вы признавать свои ошибки? Вот, Вы пишете, что «свойство экстремумов непрерывных и гладких функций, у которых в точках экстремумов функции экстремумов не имеют разрывов и являются непрерывными функциями» ложно! А я считаю это свойство экстремумов верным. Как нам быть? Вы продолжаете настаивать на этом, или Вы признаете, что в оценке необходимого условия существования экстремума непрерывной и гладкой функции (2) (непрерывности функции экстремумов) допустили ошибку!

6.03.2024, 16:37 Цорин Борис Иосифович Отзыв: {1} "функция (2) будет у нас функцией 4 переменных. Возможно, это будет точнее" - ну внесите изменение в статью, не могу запретить. Если Вы замените в статье функцию с двумя переменными и двумя параметрами на функцию с четырьмя переменными, она потеряет экстремумы в нецелых n. {2} "Возможно, это будет точнее. Это ничего не меняет!" - очень даже меняет. Параметр и переменная функции - очень разные вещи. {3} "Кто Вам сказал, что корень n0 уравнения x0^n+y0^n=z0^n, доставляет и минимум функции (2) при нецелых значениях n0" - математика сказала. Доказательство я приводил 01.03.24 19:26 мск. {4} "О каких экстремумах идет речь, когда Вы говорите, что функция (2) при нецелых значениях параметра “n” имеет экстремумы в целочисленных точках (x0, y0)" - о ненулевых минимумах. {5} "И не надо вот таких контрпримеров, как f(x)=x^2+c, (лучше было бы f(x, у)=x^2+у, но их тоже не надо)" - а почему Вы решаете, каких контрпримеров не надо и какие контрпримеры лучше? Что, еще одним следствием аксиомы Ремизова является право Ремизова на выбор контрпримеров, приводимых критиками? {6} "И не надо путать координату экстремума со значением функции в точке экстремума" - вот тут согласен, не надо, не путайте больше. {7} "Стоило задать Вам уточняющий вопрос, как Вы поплыли, вся Ваша стройная теория доказательства ошибочности нашего доказательства ВТФ посыпалась" - та Вы шо? Я, оказывается, куда-то поплыл? Во-первых, я не "поплыл", а объяснил Вам подробно суть Ваших заблуждений. Во-вторых, это было не "доказательство ошибочности", доказательство ошибочности я приводил 29.02.24 в 20:55 мск, его Вы обещали разобрать позже, но так и не приступили, а то, что мы обсуждали последние дни, - это был всего лишь один из примеров нелепости Ваших результатов. {8} "Теперь осталось проверить, способны ли Вы признавать свои ошибки?" - я способен, а Вы? {9} "Вот, Вы пишете, что «свойство экстремумов непрерывных и гладких функций, у которых в точках экстремумов функции экстремумов не имеют разрывов и являются непрерывными функциями» ложно! А я считаю это свойство экстремумов верным. Как нам быть?" - я привел Вам пример функции, для которой выдуманное Вами свойство очевидным образом неверно, и доказал, что для этой функции это "свойство" неверно. Вам пора перестать считать его верным. {10} "или Вы признаете, что в оценке необходимого условия существования экстремума непрерывной и гладкой функции (2) (непрерывности функции экстремумов) допустили ошибку!" - ну не могу же я признать ошибку там, где ее нет, даже во имя Вашего спокойствия. А что, вот это "а я считаю верным!" и требование признать ошибку там, где ее нет, это и есть весь обещанный "ответ на контрпример"?

6.03.2024, 16:43 Цорин Борис Иосифович Отзыв: Аксиоматика Ремизова, составлена по результатам наблюдений. Аксиома Ремизова: Ремизов доказал теорему Ферма. Следствие 1 из аксиомы Ремизова: Ремизов всегда прав. Следствие 2: любая функция имеет любое свойство, которое требуется Ремизову, и не имеет тех свойств, которые Ремизову мешают. Следствие 3: если кто-то смеет указывать Ремизову на его ошибки, Ремизову не нужно пытаться свои ошибки понять, ему достаточно либо придумать какое-нибудь новое свойство согласно следствию 2, либо пылко сослаться на следствие 1, желательно с восклицательным знаком. Следствие 4: Ремизов имеет право объявлять любой контрпример неподходящим и требовать его не приводить. Следствие 5: Ремизов имеет право объявлять любую аргументацию оппонентов посыпавшейся, а самих оппонентов поплывшими в любой момент, когда не хочет или не может воспользоваться следствием 2.

6.03.2024, 18:34 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, вот и настало время рассмотреть Ваш контрпример. Чтобы приводить контрпримеры, надо понимать сущность нового метода доказательства неразрешимости (разрешимости) диофантовых уравнений в целых числах. А Вы сущности метода не понимаете. Приводя свой контрпример, Вы хотели доказать ошибочность нашего доказательства ВТФ, а доказали что наше доказательство ВТФ является верным! И это благодаря Вашему контрпримеру. Сущность метода состоит в установлении целых значений параметра n, при которых диофантово уравнение будет иметь или не будет целочисленные решения. Для этого задача отыскания значений параметра n, при которых диофантово уравнение имеет целочисленные решения, заменяется эквивалентной задачей отыскания значений параметра n, при которых периодическая, непрерывная и гладкая функция будет иметь нулевые локальные минимумы. Метод применяется тогда, когда надо установить (когда неизвестно) имеет ли целочисленные решения диофантово уравнение. Другими словами, метод применяется только в тех случаях, когда в точках с целыми координатами х0, у0 и целым n переменная z не является целой (в этом случае необходимые условия существования экстремумов не удовлетворяются, а необходимое условие существования экстремумов (6) является неявным уравнением), и требуется установить может ли диофантово уравнение иметь целочисленные решения при других целых значениях переменных х0 и у0 и заданным целым n. Поэтому Ваш контрпример является контрпримером для Ваших доводов ошибочности нашего доказательства ВТФ. В случае, когда в точках с целыми координатами х0 и у0 и целым n переменная z является целой, необходимые условия существования экстремумов (4) и (5) удовлетворяются, а условие (6) не является неявным уравнением, определяющим неявную функцию (7). Для того, чтобы это понять, надо уравнения (4), (5) и (6) записать в следующем виде: -sin(2*a*pi*z)/z^(n-1)=sin(2*a*pi*x) /x^(n-1)= sin(2*a*pi*y) /y^(n-1). Когда переменная z не является целой, уравнение (6) sin(2*a*pi*x) /x^(n-1)-sin(2*a*pi*y) /y^(n-1)=0 или sin(2*a*pi*x) /x^(n-1)= sin(2*a*pi*y) /y^(n-1)<>0 является неявным уравнением, определяющим неявную функцию. Когда переменная z является целой, уравнение (6) sin(2*a*pi*x) /x^(n-1)-sin(2*a*pi*y) /y^(n-1)=0 или sin(2*a*pi*x) /x^(n-1)= sin(2*a*pi*y) /y^(n-1)=0 не является неявным уравнением, определяющим неявную функцию. В этом случае уравнение (6) эквивалентно системе двух независимых уравнений. А решение задачи эквивалентно решению системы трех уравнений - sin(2*a*pi*x) /x^(n-1)=0, sin(2*a*pi*y) /y^(n-1)=0, sin(2*a*pi*z)/z^(n-1)=0. Или целые x, y, z – это координаты нулевого локального минимума функции (2), а поэтому целые x, y, z при заданном n являются целочисленным решением диофантова уравнения Ферма (1). То есть, когда z целое, решение задачи при заданном n очевидно – диофантово уравнение Ферма (1) при заданном n имеет целочисленные решения! В случаях, когда z целое, новый метод для доказательства разрешимости диофантовых уравнений не нужен. В случаях, когда z не целое, мы не можем сразу сказать, имеет или не имеет диофантово уравнение целочисленные решения, поэтому для доказательства разрешимости (неразрешимости) диофантовых уравнений необходимо применение нового метода, то есть исследование непрерывности функций экстремумов в точках экстремумов функции (2). Теперь рассмотрим Ваш контрпример z=x^n+y^n. В Вашем случае при любых целых x, y, n переменная z целая, то есть имеет место целочисленное решение указанного диофантова уравнения при любых целых x, y, n, поэтому доказывать, что диофантово уравнение z=x^n+y^n имеет целочисленные решения, нет нужды! В этом случае новый метод решения диофантовых уравнений не может быть применен, так как уравнение sin(2*a*pi*x) /x^(n-1)-sin(2*a*pi*y) /y^(n-1)=0 не является неявным уравнением, определяющим неявную функцию. Случай n=1 Вашего контрпримера, является и частным случаем теоремы Ферма, когда n=1. В этих случаях z – целое при любых целых x, y, со всеми вытекающими последствиями, то есть никаких противоречий с новым методом решения диофантовых уравнений не имеется, и эти случаи не могут служить доказательством ошибочности нашего метода доказательства ВТФ. Господин Цорин, как поговаривал генсек Горбачев, мы с Вами не можем придти к консенсусу, поэтому нашу дискуссию следует прекратить!

6.03.2024, 20:38 Ремизов Вадим Григорьевич Отзыв: Господин Цорин, предлагаю Вам ничью!

6.03.2024, 21:52 Цорин Борис Иосифович Отзыв: {0} "Чтобы приводить контрпримеры, надо понимать сущность нового метода доказательства неразрешимости (разрешимости) диофантовых уравнений в целых числах" - неа, не надо. Я привожу контрпример не к Вашему методу в целом, а к придуманному Вами "свойству" функций. {1} "а условие (6) не является неявным уравнением, определяющим неявную функцию (7)" - так-так, погодите-ка, а как может быть, что в Вашем примере уравнение (6) определяет функцию (7), а в моем примере точно такое же уравнение не определяет точно такую же функцию? Что за мистика? При чем тут переменная z, если этой переменной в уравнении (6) нет? ) С какой это стати вдруг перестает уравнение (6) определять функцию (7) из-за какой-то там переменной, в уравнении отсутствующей? Я эту переменную вообще не вводил в своем примере. Нет, если хотите, я могу Вам привести и примеры, когда целые x и y еще не дают автоматически минимум функции при целом n и a=1, а Вами придуманное "свойство" все равно не выполняется, но Вы что-то очень странное понесли. {2} "Когда переменная z является целой, уравнение (6) sin(2*a*pi*x) /x^(n-1)-sin(2*a*pi*y) /y^(n-1)=0 или sin(2*a*pi*x) /x^(n-1)= sin(2*a*pi*y) /y^(n-1)=0 не является неявным уравнением, определяющим неявную функцию" - а Вы не замечаете, что в Вашей статье z точно так же целая в гипотетических точках экстремума? {3} "Когда переменная z является целой, уравнение (6) sin(2*a*pi*x) /x^(n-1)-sin(2*a*pi*y) /y^(n-1)=0 или sin(2*a*pi*x) /x^(n-1)= sin(2*a*pi*y) /y^(n-1)=0" - опять-таки, с какой стати от отсутствующей в уравнении переменной z зависит, будут ли равны нулю и уменьшаемое, и вычитаемое по отдельности? ) При a=1 они и у Вас равны 0, при a в окрестностях единицы они нулю не равны. {4} "диофантово уравнение Ферма (1) при заданном n имеет целочисленные решения" - не сбивайтесь на диофантово уравнение, оно тут совершенно ни при чем, свойства функции никак не зависят от того, из-за какого уравнения мы вдруг решили эту функцию исследовать. Мы обсуждаем свойства функции, а не то, можно ли ее применять для теоремы Ферма. {5} "Случай n=1 Вашего контрпримера, является и частным случаем теоремы Ферма, когда n=1" - то же самое. Свойства функции не зависят от того, применяется ли она для исследования диофантова уравнения, и можно ли это диофантово уравнение решить без этой функции. Ваши последние утверждения сводятся к "Ремизов доказал, что те диофантовы уравнения, которые не имеют решения, не имеют решения, потому что они не имеют решения, а если какое-то диофантово уравнение имеет решение, то для него нет нужды и вообще запрещено применять этот метод, а то ведь получится, что уравнение одновременно имеет решение и не имеет решений, ерунда какая-то". {6} "предлагаю Вам ничью!" - это переводится как "прекратите указывать на мои ошибки, не мешайте мне обманывать тех, кто не знает математику, включая самого себя", так, что ли? )

6.03.2024, 22:26 Цорин Борис Иосифович Отзыв: Бонусом. Раз уж сказал, что могу, так сразу и приведу. Что покажет Ваш "анализ" функции f(x,y)=sin^2(pi*a*z)+sin^2(pi*a*x)+sin^2(pi*a*y)+sin^2(pi*n), где x и y - положительные вещественные переменные, n>1 - положительный вещественный параметр, a - вещественный параметр с областью определения в точке a = 1 и ее ближайшей окрестности, а z - зависимая переменная, определяемая как z=(x^n+y^n) ^ (2.5/n)? P.S. Если по основному, предыдущему моему сообщению каким-то чудом поймете свои ошибки, то на это можете не отвечать. А если после прочтения основного сообщения Вам захочется продолжить в том же духе нести чушь про "эту функцию запрещено исследовать, так как она соответствует диофантову уравнению, у которого есть решения" и "это уравнение не задает неявную функцию, потому что переменная, которой в нем нет, целая", то сначала исследуйте эту функцию своим способом, через "функцию экстремумов". Или давайте уж сразу переходите к утверждению "методом Ремизова можно исследовать только одну совершенно конкретную функцию, свойство Ремизова выполняется только для нее, потому что именно для нее Ремизов его выдумал".

Оставить комментарий