Статья опубликована в №120 (август) 2023
Разделы: Физика
Размещена 20.08.2023. Последняя правка: 23.08.2023.
Просмотров - 531

РЕЗУЛЬТАТЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ДИНАМИКИ РАЗВИТИЯ ВИХРЕВЫХ СТРУКТУР В ТРУБАХ С ТУРБУЛИЗАТОРАМИ КВАДРАТНЫХ, ПОЛУКРУГЛЫХ И ТРЕУГОЛЬНЫХ ПОПЕРЕЧНЫХ ПРОФИЛЕЙ

Лобанов Игорь Евгеньевич

доктор технических наук

Московский авиационный институт

ведущий научный сотрудник

УДК 532.517.4 : 536.24

 

1. ВВЕДЕНИЕ. АКТУАЛЬНОСТЬ ПРИМЕНЕНИЯ ИНТЕНСИФИКАЦИИ ТЕПЛООБМЕНА В КАНАЛАХ ТРУБЧАТЫХ ТЕПЛООБМЕННЫХ АППАРАТОВ

В авиационной технике теплообменные устройства также нашли широкое применение для охлаждения элементов двигателей и конструкций летательных аппаратов, приборных отсеков и кабин самолётов. Такие теплообменники должны обладать малыми габаритными размерами и массой, должны обладать высокой эксплуатационной надёжностью.

Самым перспективным путём увеличения компактности теплообменных аппаратов является интенсификация теплообмена в каналах. Следовательно, проблема интенсификации теплообмена в каналах является актуальнейшей в данном отношении.

Имеющиеся многочисленные исследования по интенсификации теплообмена, число которых год от года растёт, постулируют противоречивые результаты. С другой стороны, методы интенсификации теплообмена, предлагаемые в вышеупомянутых исследованиях, не всегда высокоэффективны и (или) высокотехнологичны. Сложившаяся ситуация в отношении различных методов исследований интенсификации теплообмена вносит значительные затруднения в их оценку, а также обоснованный выбор эффективности метода интенсификации теплообмена. Вышесказанное редуцирует использование различных методов интенсификации теплообмена, что, в свою очередь, приводит к повышенным экономическим потерям и затормаживает дальнейшее совершенствование выпускаемой продукции, приводит к повышенной металлоёмкости последней.

Внедрение методов интенсификации теплообмена позволит существенно сократить габариты и металлоёмкость различного рода теплообменников и теплообменных устройств и, в частности, энергетических теплообменников — воздухоподогревателей и котлов и газотурбинных установок (ГТУ), различного рода подогревателей, в том числе пароперегревателей атомных электростанций (АЭС), маслоохладителей; в теплообменных устройствах, применяемых в авиационной технике для охлаждения элементов двигателей и конструкций летательных аппаратов, приборных отсеков и кабин самолётов, в частности, в системах охлаждения ГПВРД, и других устройств. При заданных массогабаритных показателях установки применение методов интенсификации теплообмена позволит значительно форсировать процесс. Внедрение методов интенсификации теплообмена в энергетическом оборудовании обеспечит значительный эффект. 

2. ОСНОВНЫЕ АСПЕКТЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ИНТЕНСИФИЦИРОВАННЫХ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ И ТЕПЛООТДАЧИ

Теоретическое математическое моделирование нестационарного потока и теплообмена в каналах с выступами различных профилей производится на тех же основах, что было реализовано в предыдущих работах [1-4].

Генерация специфического многоблочного вычислительного комплекса [1-4], основанного на разномасштабной пересекающейся структурированной сетке, при высокоэффективных и точных решений нестационарного 2-х-мерной и 3-х-мерной задачи конвективной теплоотдачи в прямом круглом канале с циклическими шероховатостями в формах выступов с однородными рабсредами на довольно  больших  отрезках  критериев  Рейнольдса  (Rе=1О⁴...1О⁶)  и  Прандтля (Рr=О,7...12).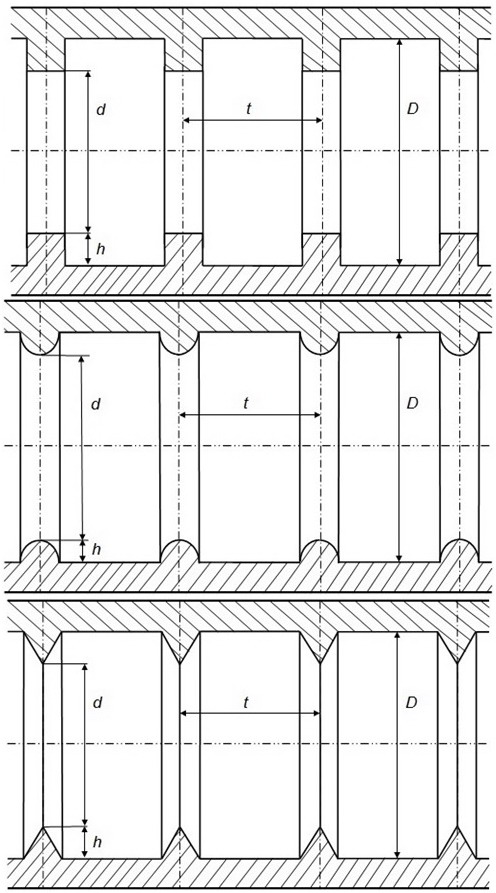



Рис. 1. Сечения прямых круглых каналов с поперечными поверхностными выступами квадратных, полукруглых и треугольных поперечных профилей соответственно.

Исходные системы диффуравнений с частными производными (Рейнольдса, Навье—Стокса) замыкаем посредством модифицированных при учёте кривизн линий тока, и ментеровским подходом, переносных функций переноса напряжений для сдвигов [1-4]. Главные исходящие данные для уравнений управления и необходимых условий на границах приведены в монографии [13].

Методологическое описание при решении исходящих уравнений содержится в основе на концептуализме расщеплений по физпроцессу процедурам при коррекциях для давления.

Основы модели были изложены в [17-19], поэтому в рамках данной статьи будет изложена лишь специфика, характерная для вычисления нестационарных потоков и теплосъёмов для трубы с выступами разнообразных профилей.

Прямая круглая труба с рёбрами (рис. 2) подразделяется секционно с расположением в их центрах, выходных и входных и гладких отрезков.

 


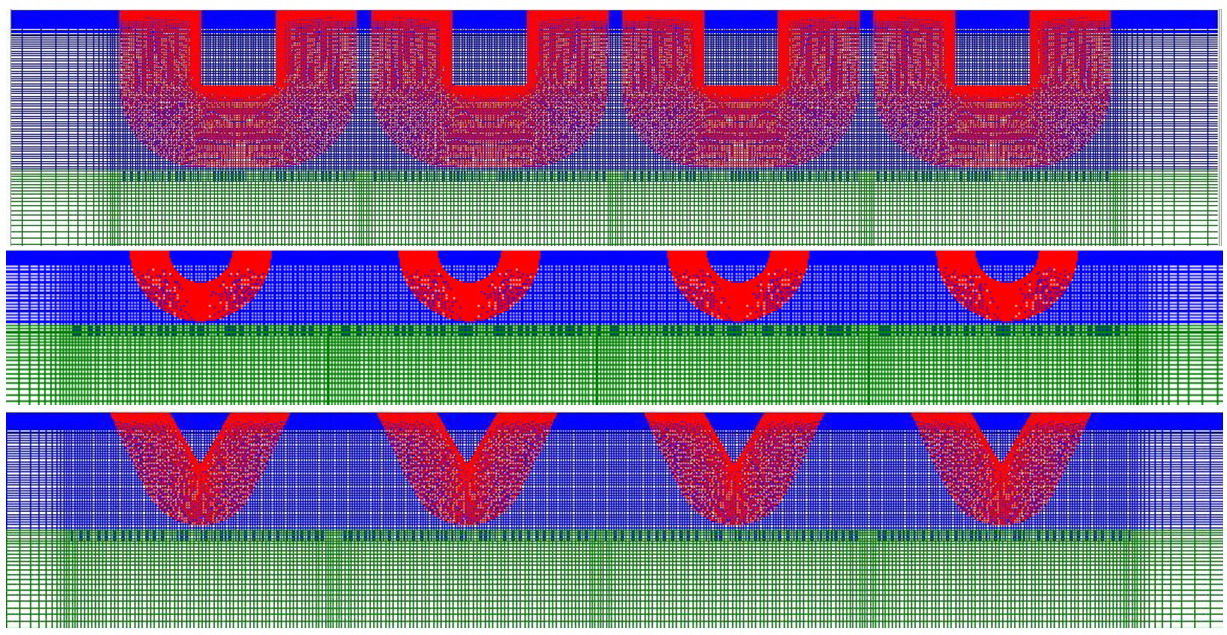
 Рис. 2. Сетка трубы, включающая несколько секций с установленным посредине выступом, выходного и входного гладких отрезков.

 

Главные направления статьи могут быть охарактеризованы нижеследующим способом: верифицирование реализованного расчётного метода для нестационарных потоков и теплосъёма в каналах с выступами с умеренными критериями Рейнольдса, которые подвергались исследованию в имеющемся экспериментальном материале [5, 6].
На основе верификаций следует сделать расчёт нестационарных потоков и теплосъёмов для достаточно общераспространённых вариантов интенсифицированных теплосъёмов в канале с выступами при квадратных, полукруглых, треугольными профилях. Далее следует проанализировать полученные результаты расчётов при выявлении специфики течений и теплоотдачи как зависимость от видов поперечных профилей.
Далее необходимо перейти к непосредственным расчётам и анализу последнего по нестационарным течениям и теплоотдаче, нестационарным вихревым структурам в каналах с выступами различных профилей: квадратного, полукруглого, треугольного.

3. РАЗВИТИЕ СМЕРЧЕВОЙ СТРУКТУРЫ В ТРУБЕ С ТУРБУЛИЗАТОРАМИ КВАДРАТНОГО, ПОЛУКРУГЛОГО И ТРЕУГОЛЬНОГО СЕЧЕНИЙ

Экспериментальные исследования, приведённые в [5, 6, 16], дают понять, что вихри в каналах с турбулизаторами может быть нестационарной для определённого диапазона течений.

Математические модели потока и теплосъёма в трубе с выступами (рёбрами), сгенерированные в работах [1-4, 7-12, 14, 15], проводились с детерминированием данных о потоке и теплосъёме при условиях стационарных (установившихся) течений. В вышеупомянутых исследованиях вычисления верифицировались опытным материалом, поэтому использование предлагаемого способа расчёта для нестационарных комплексов потоков и теплосъёмов  в прямых круглых трубах с рёбрами может быть признано обоснованным.

Вычисления нестационарных симплексов потоков и теплосъёмов в трубах с рёбрами позволяют выявлять параметры потоков, которые различаются от стационарного потока. При вычислениях следует показать временные генерации, развития, движения, распады вихря в трубе с рёбрами с разнообразными поперечными сечениями (треугольник, квадрат, полукруг).

Имеющаяся опытная информация, приведённая в [5, 6], обусловливает, что вихрь является нестационарным,  к примеру, в условиях потока водяного теплоносителя в прямоугольных каналах с рёбрами при Re=1,7·1О⁵.

Опишем нестационарный вихрь при исследуемых параметрах, когда отношение шага между рёбрами к высоте равно семи (рис. 3). В окрестностях первой и второй точек сгенерированы два вихря, скоро растущие по своим размерам. Вихрь в окрестности первой точки возрастает определённо скорее, нежели вихрь в окрестности второй точки. В то время как первый вихрь достигает по своим размерам примерно две высоты ребра, вихрь в окрестности второй точки достигает величины приблизительно единичной высоты ребра. Затем происходит генерация ослабленного вихря в окрестности третьей, а вихрь окрестности первой точки смещается к последующему ребру, потом кооптируется с вихрём в окрестности второй точки. Затем соединённый вихрь переходит через ребро, далее имеет место распад вихря. В данное время вихрь в окрестности третьей точки возрастает до величины высоты ребра и тоже диссоциирует. В дальнейшем процессы циклически воспроизводятся за генерациями нового вихря в окрестностях первой и второй точек.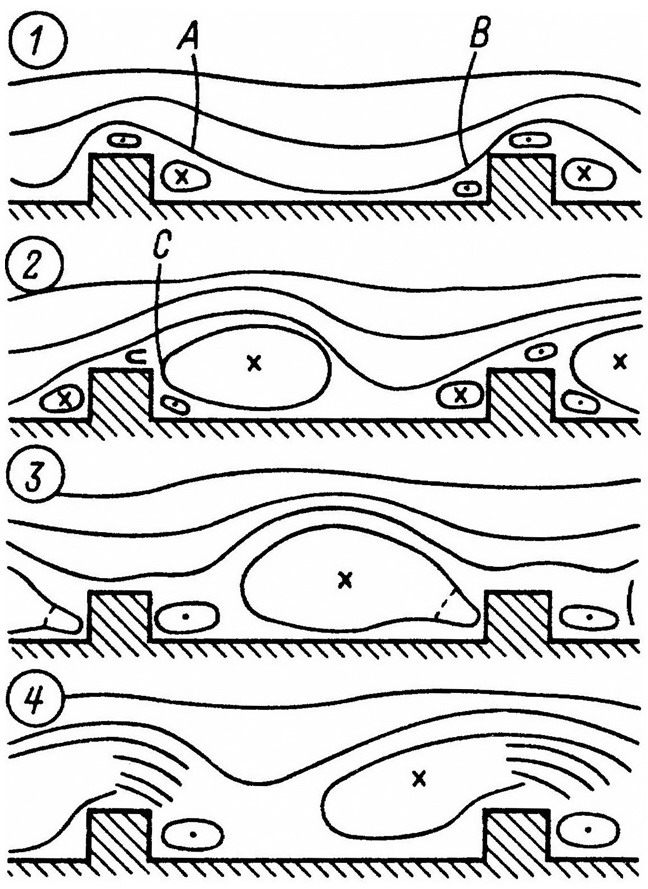



Рис. 3. Схематичное визуализирование опытов [5, 6] по динамическому развитию вихрей в водяном потоке для прямоугольного канала с квадратными рёбрами в разные временные моменты (1—4).

В рамках данного исследования было осуществлено математическое моделирование нестационарного течения и теплообмена в трубах на безе т.н. ФКОМа [1-4, 7-12, 14, 15], что с успехом использовалось при расчётах сходных стационарных случаев.

Экспериментальные исследования, проанализированные в [16], показывают, что сильные возмущения и торможение у стенки приводят к распаду ядра на крупномасштабные перевороты, которые создают выбросы на внешнем крае и биения о стенку рис. 4.




Рис. 4. Схематическая визуализация генерации закономерно чередующихся обратных токов при биении вихря о наклонную стенку.

 

Результаты расчёта нестационарного течения воздуха в трубах с рёбрами квадратного, полукруглого и треугольного поперечных сечений в периодической постановке приведены на рис. 5 для условий d/D=O,9O; t/D=O,35 (t/h=7); Re=1,7·1O⁵. Отдельные фрагменты линий тока (O—2O) на рис. 5 представлены для рёбер различных поперечных сечений для равных значений безразмерного времени.

Из рис. 5 отчётливо видна расчётная динамика развития нестационарных вихревых зон в трубе с рёбрами различных поперечных сечений.

На рис. 5 видны фрагменты генерации за квадратным рёбром нестационарного вихря, его увеличения с последующим предельным разрастанием и движением в сторону следующего ребра. Далее вышеуказанный вихрь деформируется в процессе набегания на следующий квадратный турбулизатор, после чего происходит обтекание данного квадратного турбулизатора. В дальнейшем процесс повторяется. Кроме большого вихря образуются и вихри над турбулизатором, и до турбулизатора, с которыми объединяется большой вихрь.

Для рёбер треугольного поперечного сечения деформирование большого набегающего вихря происходит уже без генерации вторичных вихрей над рёбром, как для квадратных турбулизаторов, а посредством того, что он "рассекается" угловым ребром треугольника на два вихря и обтекание треугольного ребра происходит при ощутимом забросе основного вихря в ядро потока (см.рис. 5). Вторичные вихри для треугольных рёбер образуются на гранях треугольника. Величина вторичных вихрей для квадратных рёбер больше, чем для треугольных (рис. 5).

В статьях [17-19] говорится о том, что для умеренного критерия Рейнольдса (Re около 1О⁴­) забрасывание основных вихрей в ядра течений у треугольного ребра сильнее, чем для квадратного ребра. При повышении критерия Рейнольдса (Re около 1О⁵­) для квадратного ребра забрасывание главных вихрей в ядра течений станет большим, чем у треугольного ребра как раз по причине генерирования вторичных смерчей над квадратными рёбрами. Всё это обосновывает повышение гидросопротивления в трубе с рёбрами.

Рис. 5. Развитие зон для нестационарных потоков воздуха в трубах с рёбрами квадратных, полукруглых и треугольных профилей с d/D = О,9О; t/D = О,35, Re = 1,7·1О⁵ в синхронное время.

Для рёбер полукруглых профилей деформация большого набегающих вихрей меньше, забросы основных вихрей в ядра течений тоже меньше в сравнении с квадратны и треугольным ребром (рис. 5). Вторичный вихрь у полукруглого ребра меньше в размере, чем у квадратного и треугольного рёбер, и генерируется на дуге полуокружности (рис. 5). Вышесказанное обусловливает понижение уровня гидросопротивления у полукруглого ребра по сравнению с квадратными и треугольными рёбрами при остальных одинаковых параметрах.

Как видно на рис. 5, нестационарный вихрь хорошо согласуется с соответствующим стационарным вычислением, которое было выполнено раньше для рёбер квадратных, полукруглых и треугольных профилей [1-4, 7-12, 14, 15]. Следует отметить, что системы расчётного вихря в стационарных вычислениях для трубы с рёбрами вышеупомянутых профилей есть в некотором роде математическое ожидание систем вычисленного вихря в нестационарных постановках.

Представленный диапазон расчётных данных в достаточно хорошей степени согласуются с вышеприведёнными опытным [5, 6] (определённые отличия обусловливаются тем, что в расчётах имели место исследования более общего случая потоков, чем в опытных исследованиях), что служим верификацией применённой математической модели.

Совокупности нестационарного вихря в трубе с прямоугольными или квадратными рёбрами наиболее интересны в разрезе математических моделирований, т.к. при обтеканиях рёбер сравнительно плавных очертаний может и не генерироваться 2-х-мерного вихря [5, 6] и перед ребром, а также за ребром.

Из предоставленных данных вычислениях видно, что нестационарные течения и теплосъём для трубы с рёбрами, организации структур вихря, к примеру, отрывные зоны, является эффективными средствами для искусственных турбулизаций потоков. Выработки у турбулентностей, которая явно превалирует над диссипацией, реализуется, как правило, на удалённых границах вихревых зон, на которых градиенты скоростей и турбулентное напряжение наибольшие, что может реализовываться в одно время.

В мощном вихре, возникающем до и за рёбрами с резкими очертаниями — квадратных, треугольных — диссипации турбулентных энергий соразмерна или более с выработками турбулентностей, что обосновывает большие гидропотери, поэтому нужно по возможности использовать абрютированные рёбра, — сегментные, полукруглые — где или не генерируются 2-х-мерные отрывные зоны, или комбинируют 3-х-мерные вихрь с относительными малыми зонами отрыва между рёбрами. Максимальная выработка турбулентностей за абрютированным ребром реализуется на уровнях верхних границ рёбер.

Сказанное ранее обосновывает то, что равные или избыточные над диссипациями выработки турбулентностей у рёбер с резкими очертаниями (квадратными, треугольными) и абрютированными очертаниями (полукруглыми) реализуются с определённо различных гидропотерях. Наиболее плавные (полукруглые) рёбра имеют определённо меньшие гидропотери, чем рёбра с резкими очертаниями (треугольные, квадратные). Абрютированное ребро имеет уменьшенные гидропотери, т.к. реализуются упорядоченные системы 3-х-мерного вихря с направлениями по потоку осями, и расположены вблизи стенок труб, которые и интенсифицируют теплосъём.

Произведённые по низкорейнольсовым схемам вычисления для нестационарных интенсифицированных течениях и теплосъёма в  трубе с рёбрами квадратных, полукруглых и треугольных поперечных профилей согласуются с физическими представлениями реализованного процесса [5, 6].

Успешные моделирования, сделанные в статье, нестационарного потока и теплоотдачи в трубе с рёбрами с различными поперечными сечениями на основах низкорейнольдсовых ментеровских моделей обосновывает их перспективные применения для расчётов соответствующих процессов для широких режимных диапазонов течений теплоносителей и геометрической характеристики канала с рёбрами.

4. ГЛАВНЫЕ ВЫВОДЫ

Представлены некоторые результаты комплексного математического моделирования развития структур порождённых турбулизаторами вихрей во времени в трубе с квадратными, полукруглыми и треугольными внутренними рёбрами, что максимально интересно в рассматриваемом отношении, при средних критериях Рейнольдса на основах многоблочных вычислений, базирующихся на решениях  методом ФКОМ-ов для рейнольдсового уравнения и энергетического уравнения.

 

В статье подверглись рассмотрению рёбра потоков квадратных поперечных сечений, в которых вихрь выражен в максимальной мере, а вторичный вихрь оказывает на потоки максимальные воздействия; треугольных поперечных сечений, в которых вихрь выражен в наименьшей мере а вторичный вихрь оказывает на потоки наименьшие воздействия; полукруглых поперечных сечений, в которых набегания основных вихрей реализуются при образовании малого вторичного вихря.

Произведённые данные вычислений в очень хорошей степени согласуются с имеющимся опытным материалом, что может служить верификацией применённой математической модели.

1. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодическими выступами // Проблемы газодинамики и тепломассообмена в энергетических установках: Труды XIV Школы-семинара молодых ученых и специалистов под руководством академика РАН А.И.Леонтьева. — М.: МЭИ, 2003. — T.1. — С. 57—60.
2. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодическими выступами // Вестник МАИ. — 2004. — Т. 11. — № 2. — С. 28—35.
3. Дрейцер Г.А., Исаев С.А., Лобанов И.Е. Расчёт конвективного теплообмена в трубе с периодически расположенными поверхностными турбулизаторами потока // Теплофизика высоких температур. — 2005. — Т. 43. — № 2. — С. 223—230.
4. Лобанов И.Е. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах: Дисс. … докт. техн. наук. — М.: МАИ, 2005. — 632 с.
5. Калинин Э.К., Дрейцер Г.А., Ярхо С.А. Интенсификация теплообмена в каналах. — М.: Машиностроение, 1972. — 220 с.
6. Эффективные поверхности теплообмена / Э.К.Калинин, Г.А.Дрейцер, И.З. Копп и др. — М.: Энергоатомиздат, 1998. — 408 с.
7. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том I. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением основных аналитических и численных методов. — М.: Издательство Ассоциации строительных вузов, 2009. — 405 с.
8. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том II. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением неосновных аналитических и численных методов. — М.: Издательство Ассоциации строительных вузов, 2010. — 290 с.
9. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том III. Математическое моделирование интенсифицированного теплообмена при турбулентном течении в каналах с применением многослойных, супермногослойных и компаундных моделей турбулентного пограничного слоя. — М.: МГАКХиС, 2010. — 288 с.
10. Лобанов И.Е., Штейн Л.М. Перспективные теплообменные аппараты с интенсифицированным теплообменом для металлургического производства. (Общая теория интенсифицированного теплообмена для теплообменных аппаратов, применяемых в современном металлургическом производстве.) В 4-х томах. Том IV. Специальные аспекты математического моделирования гидрогазодинамики, теплообмена, а также теплопередачи в теплообменных аппаратах с интенсифицированным теплообменом. — М.: МГАКХиС, 2011. — 343 с.
11. Лобанов И.Е. Теоретическое исследование структуры вихревых зон между периодическими, поверхностно расположенными турбулизаторами потока прямоугольного поперечного сечения // Известия вузов. Авиационная техника. — 2011. — № 4. — С. 64—66.
12. Лобанов И.Е., Калинин Э.К. Теоретическое исследование, сопоставление с экспериментом линий тока и составляющих кинетической энергии турбулентных пульсаций в вихревых структурах в трубах с турбулизаторами // Отраслевые аспекты технических наук. — 2011. — № 12. — С. 4—15.
13. Численное моделирование вихревой интенсификации теплообмена в пакетах труб / Ю.А.Быстров, С.А.Исаев, H.A.Кудрявцев, А.И.Леонтьев. — СПб: Судостроение, 2005. — 398 с.
14. Ashrafian A., Andersson H.I. Roughness Effects in Turbulent Channel Flow // Turbulence, Heat Transfer and Mass Transfer 4. — New York, Wellington (UK): Begell House Inc., 2003. — Р. 425—432.
15. Лобанов И.Е. Математическое моделирование структуры вихревых зон между периодическими поверхностно расположенными турбулизаторами потока полукруглого и квадратного поперечного сечения // Отраслевые аспекты технических наук. — 2012. — № 9. — С. 11—30.
16. Интенсификация теплообмена. Успеха теплопередачи, 2 / Ю.В.Вилемас, Г.И.Воронин, Б.В.Дзюбенко и др.; Под ред. А.А. Жукаускаускаса и Э.К. Калинина. — Вильнюс: Москслас, 1988. — 188 с.
17. Лобанов И.Е. Математическое моделирование динамики развития вихревых структур в трубах с турбулизаторами // Mосковское научное обозрение. — 2013. — № 12. — С. 9—15.
18. Лобанов И.Е. Математическое моделирование динамики развития вихревых структур в трубах с турбулизаторами // Вестник ПНИПУ. Аэрокосмическая техника. — 2014. — № 38. — C. 16—31.
19. Лобанов И.Е. Теория динамики вихревых структур в трубах с турбулизаторами // Научное обозрение. — 2015. — № 22. — С. 226—237.

Рецензии:

20.08.2023, 14:43 Ашрапов Улугбек Товфикович
Рецензия: Автор в статье пишет - "В мощном вихре, возникающем до и за рёбрами с резкими очертаниями — квадратных, треугольных — диссипации турбулентных энергий соразмерна или более с выработками турбулентностей, что обосновывает большие гидропотери, поэтому нужно по возможности использовать абрютированные рёбра, — сегментные, полукруглые — где или не генерируются 2-х-мерные отрывные зоны, или комбинируют 3-х-мерные вихрь с относительными малыми зонами отрыва между рёбрами". Однако в исследование [https://www.sciencedirect.com/science/article/abs/pii/S0017931021000983] продемонстрировано влияние конических и веретенообразных турбулизаторов, размещенных в двухтрубном теплообменнике на теплоперенос и турбулентный поток. Всего промоделировано 21 конфигураций, включая конические и веретенообразные вставки турбулизатора, в двухтрубном теплообменнике с круглой и прямоугольной конфигурациями труб при четырех уровнях числа Рейнольдса (Re = 4000, 7000, 10000 и 13000) со стороны трубы. Результаты показывают, что максимальный коэффициент конвективной теплоотдачи достигается при использовании теплообменника с круглой внутренней трубой. Кроме того, установлено, что коэффициент полезного действия теплообменника (ТО) увеличивается за счет изменения формы конических турбулизаторов на веретенообразные. Несмотря на выше сказанное, статья автора имеет научную ценность, актуальность и новизну. Рекомендую статью к публикации в журнале SCI-ARTICLE.RU.

21.08.2023, 13:20 Мирмович Эдуард Григорьевич
Рецензия: Прежде всего, наш уважаемый Улугбек Товфикович, показавший глубокое проникновение в материал статьи И.Е. Лобанова, так и не закончил рецензию своим заключением о допуске к публикации статьи. Рецензент неоднократно обращал внимание автора на необходимость указания, например, во введении, где и каким образом, в какой отрасли практической деятельности применимы результаты исследований. Читатель не может этого знать без чёткого указания автора. При заправке ракет? При перекачивании или каких-то элементах логистики жидкости и газа, углеводородов и пр. Журнал SciArtcl не узкоспециальный технический журнал, а электронная площадка для научной публицистики широкого спектра теоретических и прикладных исследований. Уважаемый Игорь Евгеньевич не реагирует на эти замечания рецензента вот уже в течение нескольких лет. Где и для какой цели используются транспортные сети с квадратными сечениями, теми или иными препятствиями - турбулизаторами? В аннотации, как правило, скобки не используются, и понятно почему. Ссылки последовательных работ даются через тире типа [1-4], [17-19], а не перечислением десятка источников. И всё же в статье не приводятся математическое, теоретическое и численное моделирование, а рассказывается о них и приводятся некоторые результаты проведенных и изложенных ранее в других работах научных исследований. На взгляд рецензента, и название статьи, и заголовок первой главы надо подкорректировать в этом отношении. В заключении лучше бы вместо "Произведены математические моделирования временных развитий структур вихря " сказать "Представлены некоторые результаты комплексного математического моделирования развития структур порождённых турбулизаторами вихрей во времени...". Очень неудачным выглядит выражение: "при высокоэффективных и точных решений нестационарного 2-х-мерного и 3-х-мерного вопроса " и по согласованию, и по смыслу, т.к. вопрос не может быть n-мерным. Но это на усмотрение автора. Без учёта замечаний рецензента на этот раз статья к печати не рекомендуется, т.к. для читателя ни актуальность, ни научная полнота не согласуются с названием. Рецензент хотел бы увидеть откорректированную статью хотя бы с частичным учётом его замечаний. Прошу извинения у очень авторитетного учёного, да ещё сотрудника любимого мной МАИ,



Комментарии пользователей:

Оставить комментарий